24.Определение колориметрии. Основные способы уравнивания цветов.

Фотометрия - это изучение меры яркости (количественное описание).

Колориметрия - это изучение цвета. Важный компонент колориметрии - уравнивание цветов.

В основе трехцветной теории цветного зрения лежит возможность представления произвольного цвета сложением в нужной пропорции трех основных цветов.

Объективное уравнивание цветов (для излучающих предметов): на поверхность идеального отражателя проецируется пятно света с произвольной спектральной плотностью. На ту же поверхность проецируется пятно опорного белого цвета, а также пересекающиеся пятна трех основных цветов. Сначала интенсивность трех основных цветов устанавливается так, чтобы общая часть пятен имела такой же цветовой тон и насыщенность, как и опорный белый цвет. Затем измеряются интенсивности трех цветов (опорные интенсивности). Далее интенсивности основных цветов устанавливают так, чтобы добиться уравнивания заданного цвета.

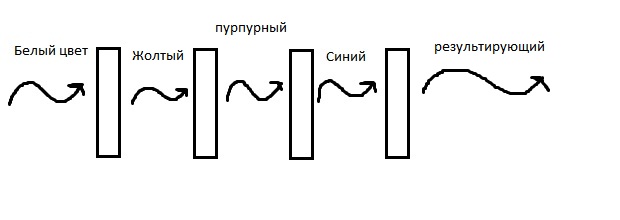
Субтрактивное уравнивание цветов (для поглощающих предметов): на первом этапе концентрации красителей трех фильтров изменяются до тех пор, пока не будет достигнуто субъективное уравнивание опорного белого цвета. Эти концентрации являются уравнивающими величинами. Затем концентрации изменяются так, чтобы обеспечить уравнивание желаемого цвета

25.Аксиомы уравнивания цветов Грассмана.

Аксиома - утверждение, принимаемое истинным без доказательств, и которое в последующем служит «фундаментом» для построения доказательств в рамках какой-либо теории, дисциплины и т.д. Аксиомы уравнивания цветов:

1:Любой цвет может быть уравнен смесью не менее, чем трех любых цветов. Коэффициенты могут быть и положительными и отрицательными.

2:Уравнивание, достигнутое при данных интенсивностях цвета, сохраняется в широком диапазоне интенсивностей.

3:Смесь цветов не может быть разделена человеческим глазом на отдельные компоненты.

4:Яркость (светлота) смеси цветов равна сумме яркости её компонентов.

5: Закон сложения цветов.

Если цвет M эквивалентен цвету N , а цвет P эквивалентен Q , то смесь цветов M+P эквивалентна смеси N+Q.

M = N ; P = Q ; M + P = N + Q ;

6: Закон вычитания цветов. Если M + P = N + Q и известно, что P = Q , то M = N (обратное пункту 5)

7: Закон транзитивности. Если M = N ; N = P , то M = P.

8:Аксиома представляет собой рассуждения об уравнивании цветов:

- со всеми положительными коэффициентами;

- с одним отрицательным коэффициентом;

- с двумя отрицательными коэффициентами.

26. Цветовое пространство.Координаты цвета и координаты цветности.

Координаты цвета можно рассматривать как координаты точек в некотором трехмерном пространстве.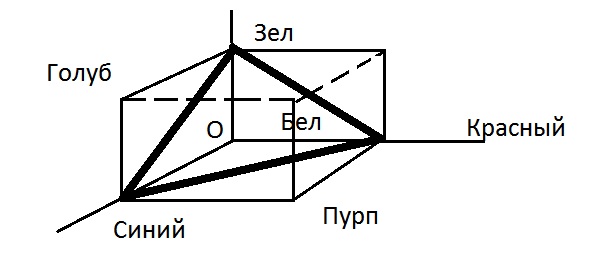

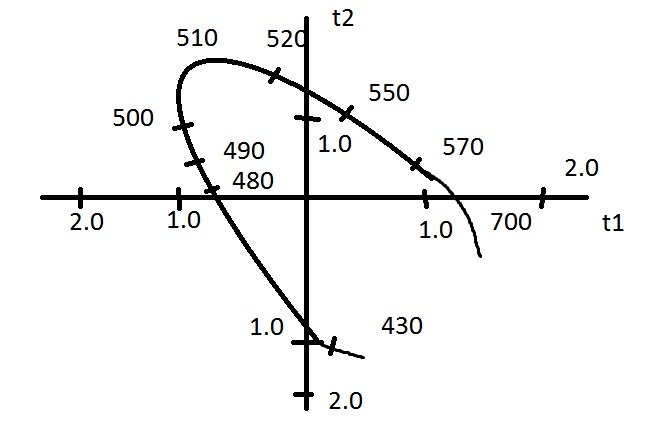
Треугольник в кубе - треугольник Максвела. Координаты цветности меняются от 0 до 1. С помощью реальных источников света можно физически воспроизводить только те цвета, которые находятся внутри треугольника.

t1= T1/(T1+T2+T3)

С помощью реальных источников света можно физически воспроизводить только те цвета, которые находятся внутри треугольника. График цветностей: