22. Логарифмическая модель одноцветного зрения. Основные зрительные явления.

Зрительные явления - контрастная чувствительность, полосы маха, одновременных контраст, цветовая адаптация, зрительные иллюзии.

Контрастная чувствительность - способность улавливать минимальные различия в освещенности двух соседних областей, а также дифференцировать их по яркости

П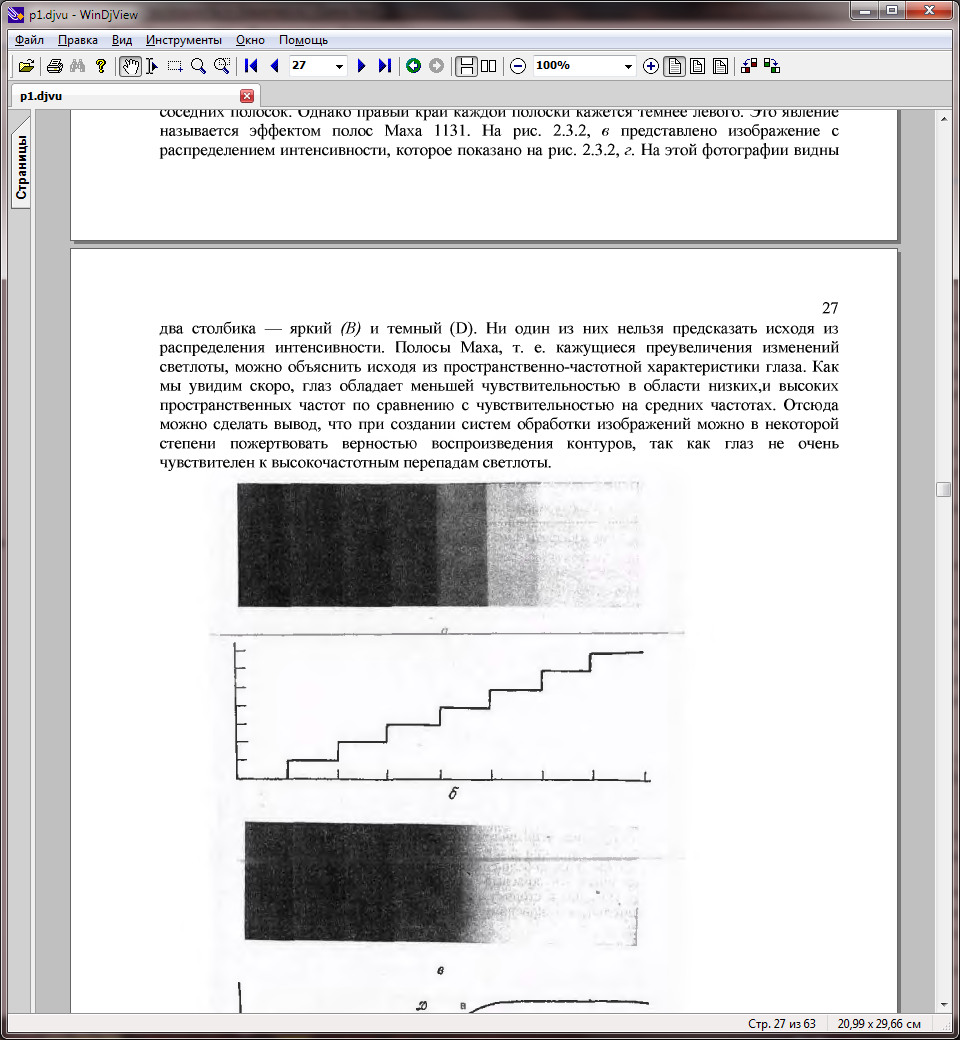 олосы Маха. Рассмотрим ступенчатый оптический клин (набор полосок различной светлоты). Интенсивность света, одинакова по ее ширине и отличается на постоянную величину от интенсивности света от соседних полосок. Однако правый край каждой полоски кажется темнее левого. Это явление называется эффектом полос Маха. Кажущиеся преувеличения изменений светлоты, можно объяснить исходя из пространственно-частотной характеристики глаза. Глаз обладает меньшей чувств. в области низких и высоких пространственных частот по сравнению с чувств. на средних частотах. Вывод: при создании систем обработки изображений можно в некоторой степени пожертвовать верностью воспроизведения контуров, так как глаз не очень чувствителен к высокочастотным перепадам светлоты.

О дновременный контраст. В действительности все маленькие квадраты имеют одинаковую яркость, но из-за разной яркости фона кажется, что их яркость разная. Цветовой фон пятна света зависит также от цвета окружения. Белое пятно на черном квадрате кажется желтоватым, если вся фигура окружена синим фоном.

Цветовая адаптация - процесс приспособления работы зрительного механизма к условиям изменённой цветности освещения наблюдаемых объектов. Воспринимаемый цветовой фон зависит от адаптации зрителя. Американский флаг, например, не сразу будет восприниматься как красно-бело-синий, если человек перед этим смотрел на интенсивный красный свет. Воспринимаемые цвета флага будут смещены в сторону голубого цвета, который является дополнительным к красному.

22.2

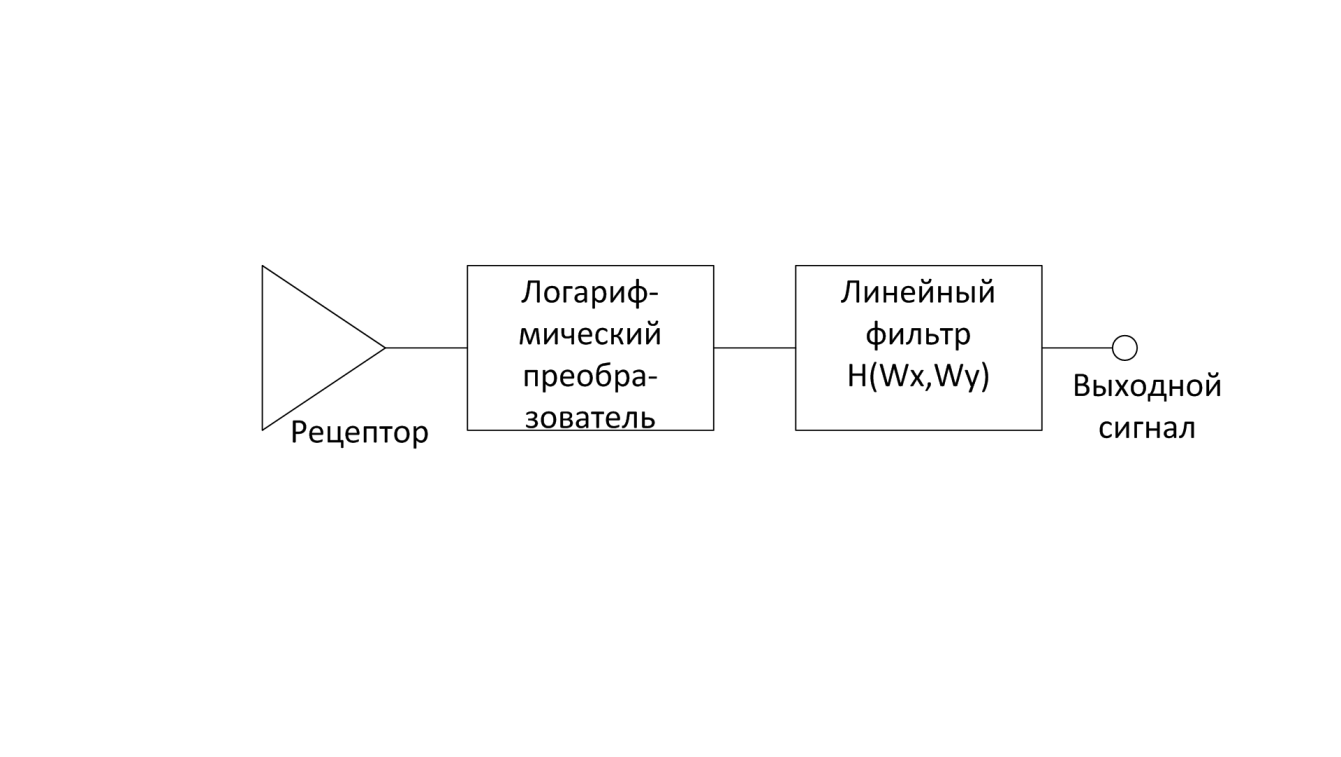
Упрощенная логарифмическая модель одноцветного зрения. Логарифмическая линейная модель позволяет удовлетворительно предсказать реакцию зрительной системы в широком диапазоне интенсивности, однако на высоких пространственных частотах и очень низких или очень высоких интенсивностях наблюдаемая реакция отличается от предсказанной на основе этой модели.

Расширенная логарифмическая модель одноцветного зрения.

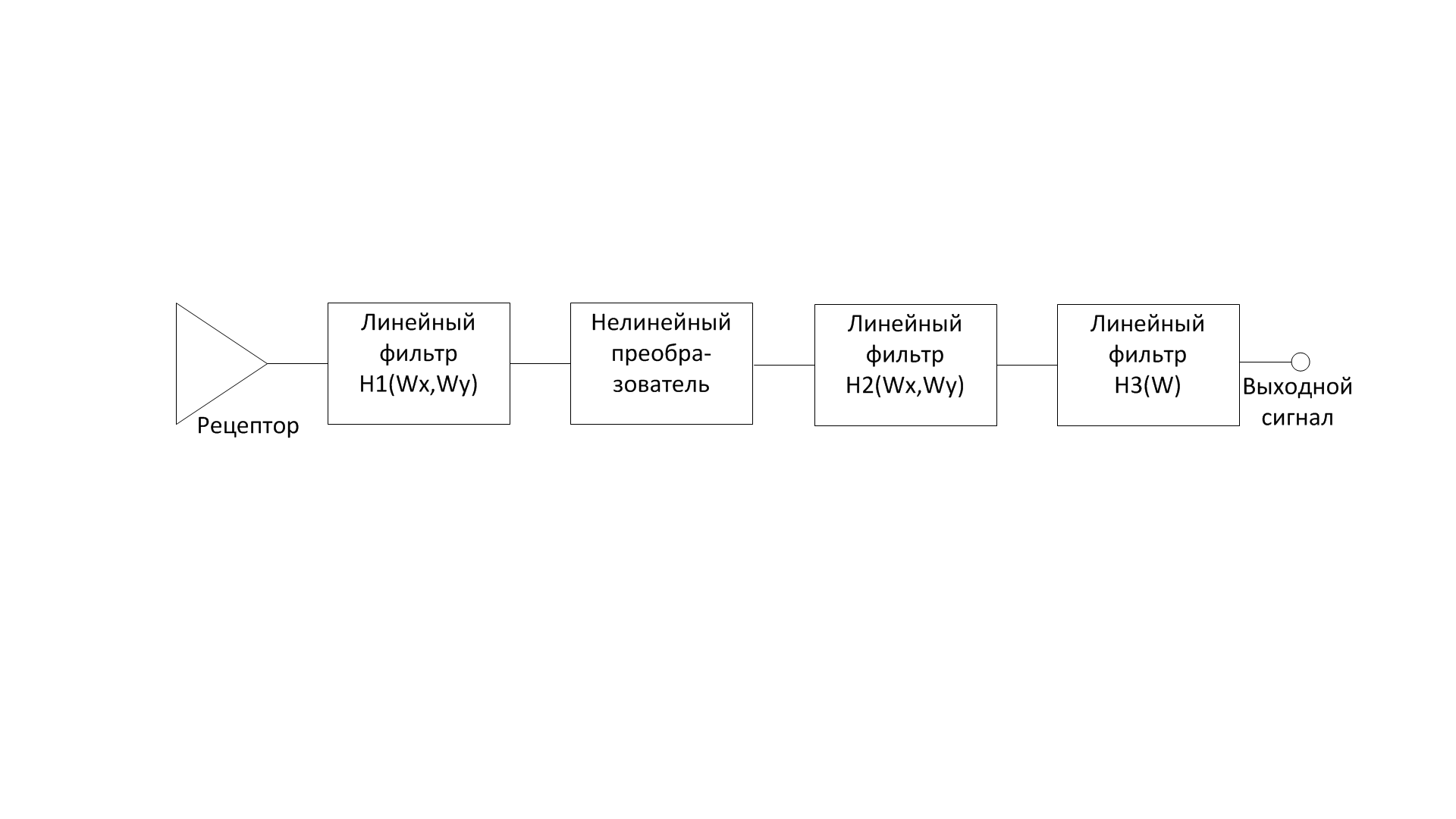
В этой модели выходной сигнал рецептора подается на вход линейного фильтра нижних частот соответствующего оптике глаза. Далее преобразователь моделирует нелинейную реакцию рецептора на изменение интенсивности. Процесс латерального торможения учитывается H2. H3 - моделирует эффект временной фильтрации.

23. Модель цветного зрения.

Логарифмическая модель цветного зрения Фрея. Выделяются колбочки 3 типов: поглощающие зеленый, желто-зеленый и синий свет.

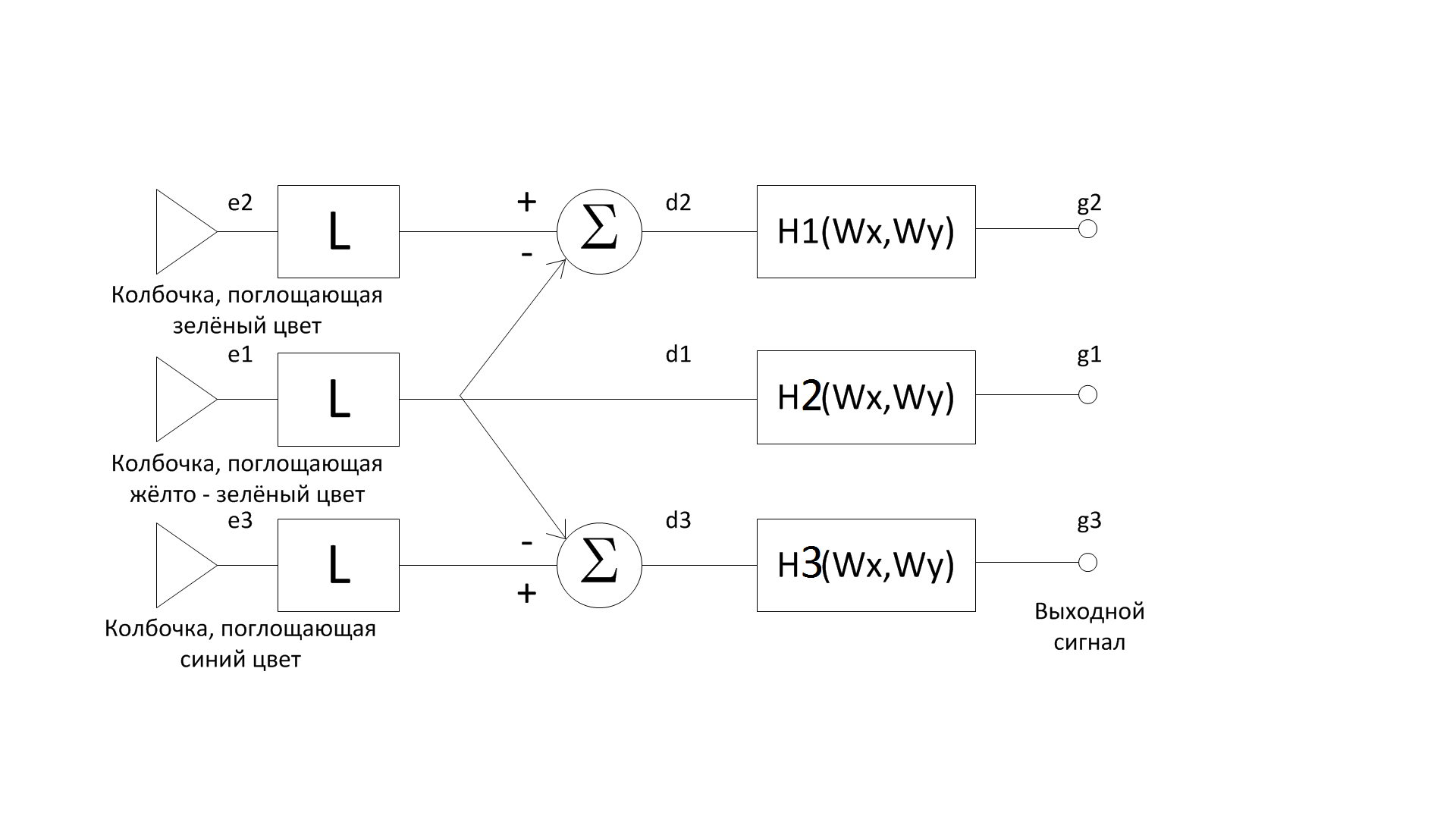
В этой модели 3 рецептора со спектральными чувствительностями s1( ), s2( ), s3( ), соответствующими 3-ем пигментам колбочек сетчатки. Сигналы е1, е2, е3 подвергаются логарифмическому преобразованию и объединяются так, чтобы получились сигналы

Далее эти сигналы проходят на линейные фильтры H1(),H2(),H3(). Получаемые на выходе сигналы g1, g2, g3 определяют восприятие цветов в мозге.

d1и d2 характеризуют цветность, а сигнал d1 пропорционален яркости.

Аналогично модели одноцветного зрения, логарифмическая модель цветного зрения может быть дополнена линейными фильтрами, которые включаются после рецепторов. Вместо логарифмической функции можно использовать нелинейную функцию общего вида.