13

Объяснение явления электромагнитной индукции с помощью электронной теории. Возникновение электродвижущей силы индукции может быть обусловлено сторонними силами разной физической природы. При движении проводника в постоянном магнитном поле сторонняя сила обусловлена силой Лоренца, с которой магнитное поле действует на движущиеся вместе с проводником электрические заряды.

Рассмотрим сначала простейший случай, когда два параллельных проводника АВ и СD (рис. 6.3) помещены в постоянное однородное магнитное поле, перпендикулярное к плоскости чертежа и направленное к нам. Слева провода AB и CD замкнуты, справа – разомкнуты. Вдоль проводов перпендикулярно магнитному полю и самому себе может свободно скользить проводящий мостик ВС. В нейтральном проводнике содержится равное количество положительных и отрицательных зарядов. Они вынуждены двигаться вместе с проводником в магнитном поле так, что на каждый из них действует магнитная сила Лоренца:

.

На рис. 6.3 мостик движется вправо со скоростью  , поэтому на положительные ионы действуют силы, направленные вниз, а на отрицательные электроны – вверх. В результате электроны начнут перемещаться по мостику вверх, и по нему потечет индукционный ток, направленный вниз. Перераспределившиеся заряды создадут электрическое поле, которое возбудит токи в остальных участках контура ABCD. Сила Лоренца играет в данном случае роль сторонней силы, возбуждающей электрический ток.

За время   поток вектора магнитной индукции изменится на  , где   – длина мостика,   – его перемещение. Электродвижущая сила индукции в соответствии с законом Фарадея будет равна

.

(6.2)

Величина   есть приращение площади контура ABCD в единицу времени. Знак минус означает, что сторонние силы направлены против положительного направления обхода контура, определяемого вектором   по правилу правого винта.

Результат справедлив и в том случае, когда однородное магнитное поле   направлено под любым углом к плоскости контура АВСD. В этом случае вектор   можно представить в виде суммы тангенциальной   и нормальной   составляющих к плоскости контура  . Вектор   вызывает лишь перераспределение электрических зарядов поперек мостика, но тока не дает. Ток определяется только нормальной составляющей  , поэтому электродвижущая сила также определяется формулой (6.2).

Полученную формулу (6.2) для электродвижущей силы индукции можно распространить на случай любого замкнутого контура, движущегося произвольным образом в постоянном неоднородном магнитном поле. Для этого надо мысленно разбить контур на очень малые участки и рассмотреть движение каждого из них. При очень малом перемещении каждого из таких участков магнитное поле, в котором он движется, можно считать однородным. Поэтому электродвижущая сила, действующая между концами участка, может быть представлена выражением (6.2), полученным для однородного поля. Путем суммирования таких выражений получится формула того же вида, в которой под   следует понимать полную электродвижущую силу, действующую в контуре, а под   – скорость изменения магнитного потока через любую поверхность, натянутую на контур.

Итак, возбуждение электродвижущей силы индукции при движении контура в постоянном магнитном поле объясняется действием магнитной силы, которая возникает при движении проводника. Эти идеи лежат в основе действия всех индукционных генераторов тока, в которых ротор с обмоткой вращается во внешнем магнитном поле.

14

Самоиндукция — это явление возникновения ЭДС индукции в проводящем контуре ^[1]при изменении протекающего через контур тока.

При изменении тока в контуре пропорционально меняется^[2] и магнитный поток через поверхность, ограниченную этим контуром^[3]. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС.

Это явление и называется самоиндукцией. (Понятие родственно понятию взаимоиндукции, являясь как бы его частным случаем).

Направление ЭДС самоиндукции всегда оказывается таким, что при возрастании тока в цепи ЭДС самоиндукции препятствует этому возрастанию (направлена против тока), а при убывании тока — убыванию (сонаправлена с током). Этим свойством ЭДС самоиндукции сходна с силой инерции.

Величина ЭДС самоиндукции пропорциональна скорости изменения силы тока  :

.

Индукти́вность (или коэффициент самоиндукции) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность^[1], краем которой является этот контур.^[2][3][4].

В формуле

 — магнитный поток,   — ток в контуре,   — индуктивность.

• Нередко говорят об индуктивности прямого длинного провода(см.). В этом случае и других (особенно - в не отвечающих квазистационарному приближению) случаях, когда замкнутый контур непросто адекватно и однозначно указать, приведенное выше определение требует особых уточнений; отчасти полезным для этого оказывается подход (упоминаемый ниже), связывающий индуктивность с энергией магнитного поля.

Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока^[4]:

.

Из этой формулы следует, что индуктивность численно равна ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.

При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого этим током^[4]:

.

Явление возникновения э.д.с. в одном из контуров при изменении силы тока в другом называется взаимной индукцией. Коэффициенты пропорциональностиL₂₁ и L₁₂ называются взаимной индуктивностью контуров. Расчеты, подтверждаемые опытом, показывают, что L₂₁ и L₁₂ равны друг другу, т. е.

        

Взаимоиндукция (взаимная индукция) — возникновение электродвижущей силы (ЭДС индукции) в одном проводнике вследствие изменения силы тока в другом проводнике или вследствие изменения взаимного расположения проводников. Взаимоиндукция — частный случай более общего явления — электромагнитной индукции. При изменении тока в одном из проводников или при изменении взаимного расположения проводников происходит изменение магнитного потока через (воображаемую) поверхность, "натянутую" на контур второго, созданного магнитным полем, порожденным током в первом проводнике, что по закону электромагнитной индукции вызывает возникновение ЭДС во втором проводнике. Если второй проводник замкнут, то под действием ЭДС взаимоиндукции в нём образуется индуцированный ток. И наоборот, изменение тока во второй цепи вызовет появление ЭДС в первой. Направление тока, возникшего при взаимоиндукции, определяется по правилу Ленца. Правило указывает на то, что изменение тока в одной цепи (катушке) встречает противодействие со стороны другой цепи (катушки).

Чем большая часть магнитного поля первой цепи пронизывает вторую цепь, тем сильнее взаимоиндукция между цепями. С количественной стороны явление взаимоиндукции характеризуется взаимной индуктивностью (коэффициентом взаимоиндукции, коэффициентом связи). Для изменения величины индуктивной связи между цепями, катушки делают подвижными. Приборы, служащие для изменения взаимоиндукции между цепями, называются вариометрами связи.

15

При всяком изменении силы тока в проводящем контуре возникает э. д. с. самоиндукции, в результате чего в контуре появляются дополнительные токи, называемые экстратоками самоиндукции. Экстратоки самоиндукции, согласно правилу Ленца, всегда направлены так, чтобы препятствовать изменениям тока в цепи, т. е. направлены противоположно току, создаваемому источником. При выключении источника тока экстратоки имеют такое же направление, что и ослабевающий ток. Следовательно, наличие индуктивности в цепи приводит к замедлению исчезновения или установления тока в цепи.

Рассмотрим процесс выключения тока в цепи, содержащей источник тока с э.д.с.  , резистор сопротивлением R и катушку индуктивностью L. Под действием внешней э. д. с. в цепи течет постоянный ток

(Внутренним сопротивлением источника тока пренебрегаем).

В момент времени t=0 отключим источник тока. Ток в катушке индуктивностью L начнет уменьшаться, что приведет к возникновению э.д.с. самоиндукции   препятствующей, согласно правилу Ленца, уменьшению тока. В каждый момент време­ни ток в цепи определяется законом Ома I= _s/R, или

                                                          (127.1)

Разделив в выражении (127.1) переменные, получим   Интегрируя это уравнение по I (от I₀ до I) и t (от 0 до t), находим ln (I /I₀) = –Rt/L, или

                                                 (127.2)

где =L/R — постоянная, называемая временем релаксации. Из (127.2) следует, что  есть время, в течение которого сила тока уменьшается в е раз.

Таким образом, в процессе отключения источника тока сила тока убывает по экспоненциальному закону (127.2) и определяется кривой 1 на рис. 183. Чем больше индуктивность цепи и меньше ее сопротивление, тем больше  и, следовательно, тем медленнее уменьшается ток в цепи при ее размыкании. При замыкании цепи помимо внешней э. д. с.   возникает э. д. с. самоиндукции   препятствующая, согласно правилу Ленца, возрастанию тока. По закону Ома,   или

Введя новую переменную преобразуем это уравнение к виду

где  — время релаксации.

В момент замыкания (t=0) сила тока I = 0 и u = –  . Следовательно, интегрируя по и (от –  до IR– ) и t (от 0 до t), находим ln[(IR– )]/–  = —t/, или

                                                        (127.3)

где   — установившийся ток (при t).

Таким образом, в процессе включения источника тока нарастание силы тока в цепи задается функцией (127.3) и определяется кривой 2 на рис. 183. Сила тока возрастает от начального значения I=0 и асимптотически стремится к установившемуся значению  . Скорость нарастания тока определяется тем же временем релаксации =L/R, что и убывание тока. Установление тока происходит тем быстрее, чем меньше индук­тивность цепи и больше ее сопротивление.

Оценим значение э.д.с. самоиндукции  , возникающей при мгновенном увеличении сопротивления цепи постоянного тока от R₀ до R. Предположим, что мы размыкаем контур, когда в нем течет установившийся ток  . При размыкании цепи ток изменяется по формуле (127.2). Подставив в нее выражение дляI₀ и , получим

Э.д.с. самоиндукции

т. е. при значительном увеличении сопротивления цепи (R/R₀>>1), обладающей боль­шой индуктивностью, э.д.с. самоиндукции может во много раз превышать э.д.с. источника тока, включенного в цепь. Таким образом, необходимо учитывать, что контур, содержащий индуктивность, нельзя резко размыкать, так как это (возникнове­ние значительных э.д.с. самоиндукции) может привести к пробою изоляции и выводу из строя измерительных приборов. Если в контур сопротивление вводить постепенно, то э.д.с. самоиндукции не достигнет больших значений.

16

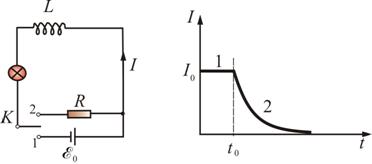
Рис. 5.6

      Сначала замкнем соленоид L на источник ЭДС   , в нем будет протекать ток   . Затем в момент времени    переключим ключ в положение 2 – замкнем соленоид на сопротивлениеR. В цепи будет течь убывающий ток I. При этом будет совершена работа:    ,  или

       

,

(5.5.1)

      Эта работа пойдет на нагревание проводников. Но откуда взялась эта энергия? Поскольку других изменений, кроме исчезновения магнитного поля в окружном пространстве, не произошло, остается заключить, что энергия была локализована в магнитном поле. Значит, проводник с индуктивностью L, по которой течет ток I, обладает энергией

,

(5.5.3)

      Выразим энергию магнитного поля через параметры магнитного поля. Для соленоида:

 .

 ; отсюда 

      Подставим эти значения в формулу (5.5.3):

,

(5.5.4)

      Обозначим w – плотность энергии, или энергия в объеме V, тогда

,

(5.5.5)

      но т.к.   , то

или

(5.5.6)

      Энергия однородного магнитного поля в длинном соленоиде может быть рассчитана по формуле

,

(5.5.7)

а плотность энергии

,

(5.5.8)

      Плотность энергии магнитного поля в соленоиде с сердечником будет складываться из энергии поля в вакууме и в магнетике сердечника: