«Назарбаев Зияткерлік мектептері» ДББҰ

Үлгі

2012-2013 оқу жылында физика-математика бағытындағы

Назарбаев Зияткерлік мектептеріндегі жоғары мектепті бітірушілерді қорытынды аттестаттауға арналған математика пәнінен

емтихан (жазба) жұмысы

1. Жазба жұмысының құрылымы

Жоғары мектепті бітірушілердің математика пәні бойынша дайындық деңгейін өлшеу ретінде емтихан жұмысының тапсырмалары қолданылады. Емтихан жұмысы үш бөлімнен тұрады және бір бірінен мазмұны, қиындығы және саны бойынша ерекшеленетін 20 тапсырмадан тұрады.

1 Бөлім базалық деңгейдегі 13 тапсырмадан тұрады, олардың белгіленуі Б1, Б2, … , Б13.

Б1-Б10 тапсырмалары – ұсынылған бес жауаптың ішінен дұрыс бір жауапты таңдауға арналған тестік тапсырма.

Б11-Б13 тапсырмалары – қысқа жауапты қажет ететін ашық түрдегі тапсырма.

2 Бөлім ортадан жоғары деңгейдегі толық жауапты қажет ететін ашық түрдегі 5 тапсырмадан тұрады, олардың белгіленуі О14, О15, О16, О17,О18.

3 Бөлім жоғары деңгейдегі толық жауапты қажет ететін ашық түрдегі 2 тапсырмадан тұрады, олардың белгіленуі Ж19, Ж20.

2. Жазба жұмысын бағалау жүйесі

Барлық жұмыс үшін қойылатын ең жоғары балл – 48 балл.

1- бөлім тапсырмаларын бағалау критерийлері

Б1–Б10 тапсырмаларының әрқайсының дұрыс жауабы 1 балмен, ал Б11 - Б13 тапсырмаларының әрқайсысы 2 балмен бағаланады.

2 Және 3 - бөлім тапсырмаларын бағалау критерийлері

П14 - П18 тапсырмаларының әрқайсының толық және дұрыс жауабы 4 балмен бағаланады. 3 бөлімнің Ж19 және Ж20 тапсырмаларының әрқайсысы 6 балмен бағаланады. Толық жауапты қажет ететін тапсырмаларды орындауға қойылатын талаптар: шешуі қажетті түсіндірмелер мен негіздеулерден тұратын математикалық тілде сауатты жазылуы керек, шешімі толық, барлық мүмкін жағдайлар қарастырылып, ескерілуі тиіс. Шешу әдісі, шешімі, жазу формасы және жауапты жазу формасы әр түрлі болуы мүмкін. Шешімі толық негізделіп, дұрыс жауабы алынған тапсырмаға ең жоғары балл беріледі. Ал дұрыс жауабы жазылып, бірақ шешімі жоқ тапсырма үшін 0 балл қойылады. Шешімді тұжырымдаудың толықтығы мен негізделуі таңдаған шешім әдісінен тәуелсіз бағаланады.

3. Балдарды бағаға көшіру шкаласы

«5» бағасы «4» бағасы «3» бағасы «2» бағасы

90 – 100 % 75 – 89 % 51 – 74 % 50 % және одан төмен

43 - 48 балл 36 - 42 балл 25 - 35 балл 24 балл және одан төмен

4. Тапсырманы орындау уақыты 300 минут немесе 5 сағат.

Емтихан жұмысы тапсырмаларының үлгісі

1 - Бөлім

Б1. Бассейн екі құбырмен 4 сағатта толады. Бірінші құбыр бассейнді 5 сағатта толтырса, екінші құбыр бассейнді қанша сағатта толтырады?

1. 15 сағат;

2. 25 сағат;

3. 10 сағат;

4. 20 сағат;

5. 30 сағат.

Б2. 1 суретте 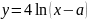функциясының графигі бейнеленген. Дұрыс жауапты таңдаңыз:

А) «а-ның мәні 5-ке тең, ал асимптотаның теңдеуі: х = 5»;

В) «а-ның мәні 5-ке тең, ал асимптотаның теңдеуі: х = 6»;

С) «а-ның мәні 6-ға тең, ал асимптотаның теңдеуі: х = 5»;

D) «а-ның мәні 6-ға тең, ал асимптотаның теңдеуі: х = 6»;

5. «а-ның мәні 5-ке тең, ал асимптотаның теңдеуі: у = 5».

Б3. Ауданы 12-ге тең АВС үшбұрышында АМ медианасы жүргізілген. Осы медиананың бойында АК:КМ=1:2 қатынасы орындалатындай К нүктесі алынған. АВК және ВКМ үшбұрыштарының аудандары неге тең?

1. 1,5 және 3;

2. 2 және 6;

3. 2 және 3;

4. 2,5 және 4;

5. 2 және 4.

Б4. 45 тонна жүкті 1300 км жерге транспортпен жеткізу үшін үш тасымалдаушы – фирманың қызметін қолдануға болады. Әр тасымалдаушы автокөліктің тасымал құны мен оның жүккөтергіштігі кестеде көрсетілген. Ең арзан тасымалға қанша теңге төлеу керек?

Тасымал даушылар	Бір автокөліктің тасымал құны (100 км-ге сәйкес теңге.)	Автокөліктің жүккөтергіштігі(тонна)
А	3200	3,5
Б	4100	5
В	9500	12

А) 540800 тг

В) 520800 тг

С) 494000 тг

D) 485000 тг

E) 479700 тг

Б5. 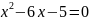квадрат теңдеуінің түбірлері 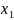және . Онда өрнегінің мәні:

1. ;

2. ;

3. ;

4. ;

5. .

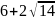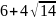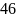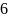Б6. п-бұрышты дұрыс көпбұрыштың бір бұрышы 135⁰. п-нің мәні:

1. 16;

2. 14;

3. 12;

4. 10;

5. 8.

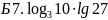өрнегінің мәні:

1. 3;

2. ;

3. ;

4. ;

5. .

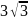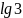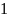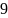функциясының графигіне жүргізілген жанама түзуіне параллель. Жанасу нүктесінің координаталарының қосындысы:

1. 1,8;

2. 2;

3. 3;

4. 3,5;

5. 12.

Б9. МАВС пирамидасының табаны – тікбұрышты АВС үшбұрышы. 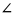С = 90⁰,

ВС = а, А = 30⁰. Пирамиданың бүйір қырлары табанымен 60⁰ бұрыш жасайды. Пирамиданың биіктігі:

1. а;

2. 2а;

3. а ;

4. а ;

5. .

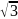Б10. Мектеп оркестрі орта және жоғары сыныптардың оқушыларынан құралған. Музыканттардың 40%-ы – ұлдар. Ұлдардың 30%-ы орта сыныптан. Қыздардың да 50%-ы орта сыныптан. Кездейсоқ алынған музыканттың орта сыныптың оқушысы болу ықтималдығы:

1. 0,41;

2. 0,42;

3. 0,43;

4. 0,5;

5. 0,53.

Б11. Көлбеу үшбұрышты призманың екі жақтарының аудандары – 70 см² және 150 см², ал олардың арасындағы бұрыш – 60⁰. Бүйір қыры – 10 см. Призманың бүйір бетінің ауданын табыңыз.

Жауабы: 350 см²

Б12. Тежеуіші бар маховик t с уақытта 3t – 0,01t² (рад) бұрышқа бұрылады. Қандай уақыт мезетінде маховик тоқтайды?

Жауабы: 150 с немесе 2,5 мин .

***

Б13. Әрбір с бірінші шаңғы тебуші екінші шаңғы тебушіден 2 мин тез өтеді. 1 сағаттан кейін бірінші шаңғышы екіншісінен бір айналымға озып кетті. Әрбір шаңғы тебуші айналымды қанша уақытта өтеді?

Жауабы 10 мин, 12 мин.

1- бөлім тапсырмаларын бағалау критерийлері

Б1–Б10 тапсырмаларының әрқайсының дұрыс жауабы 1 балмен, ал Б11 - Б13 тапсырмаларының әрқайсысы 2 балмен бағаланады.

Тапсырмалар	Балл
Б1	1
Б2	1
Б3	1
Б4	1
Б5	1
Б6	1
Б7	1
Б8	1
Б9	1
Б10	1

Тапсырма	Бағалау критерийлері	Балдар	Ең жоғарғы балл
Б11	Есеп шешуі планиметриялық есепті шешуге келтіріледі	1	2
	Дұрыс жауабы алынған	1
Б12	Есеп шешуі теңсіздікті шешуге келтіріледі	1	2
	Дұрыс жауабы алынған	1
Б13	Есеп шешуі мәселе есептің математикалық моделін құра білуге және қарапайым теңдеуді шешуге келтіріледі.	1	2
	Дұрыс жауабы алынған	1

2. – Бөлім

О14. 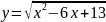функциясының ең кіші мәнін табыңыз.

Шешуі. Толық квадратқа келтірейік: .

Осыдан: . 

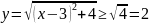Сондықтан функция 3 нүктесінде ең кіші мәнге ие болады, ол мән 2-ге тең. 

Жауабы: 2.

***

О15. Теңдеуді шешіңіз: .

Шешуі.

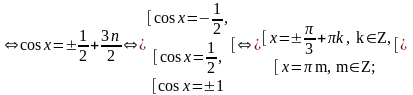
Жауабы: **

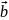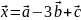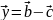О16. , және векторлары берілген. . және векторларының арасындағы бұрышты табыңыз.

Шешуі. Векторлардың арасындағы бұрышты скалярлық көбейтінді арқылы анықтайық: .

.

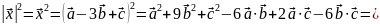
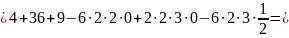
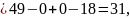
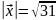Дәл жоғарыдағыдай: .

.

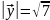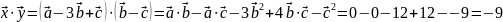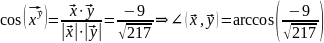немесе

.

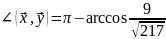Жауабы: .

***

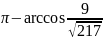О17. Теңсіздіктің бүтін шешімдерінің санын табыңыз

.

Шешуі

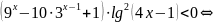
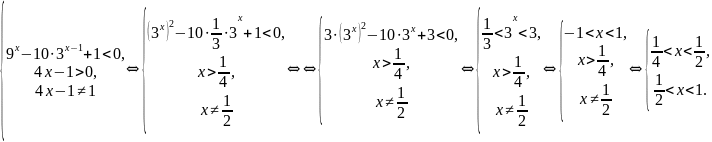
Осылайша, бұл теңсіздіктің бүтін шешімдері жоқ.

Жауабы: бүтін шешімдері жоқ.

***

О18. Трапецияның табанындағы бұрыштары 40⁰ және 50⁰. Трапецияның орта сызығы 4, ал табандарының орталарын қосатын кесіндінің ұзындығы 1-ге тең. Трапецияның үлкен табанының ұзындығын табыңыз.

Шешуі: 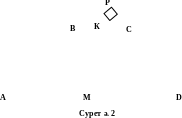Трапеция табандарының орта нүктелері және оның диагональдарының қиылысу нүктесі, сонымен қатар бүйір қабырғаларын жалғастырғандағы қиылысу нүктесі бір түзудің бойында жататыны белгілі. Олай болса, АРD және ВРС үшбұрыштары (2-сурет) – тік бұрышты, ал РК және РМ олардың гипотенузаға жүргізілген медианалары. РК = х деп алсақ, онда ВС = 2х, РМ = х + 1, АD = 2х + 2. Екінші жағынан трапецияның табандарының ұзындықтарының қосындысы 8, ал АD = 8 – 2х. Алынған теңдеуді шешеміз:

2х + 2 = 8 – 2х,

х = 1,5.

Сонымен, АD = 5.

Жауабы: 5.

2- бөлім тапсырмаларын бағалау критерийлері

Тапсыр ма №	Бағалау критерийлері	Балдар	Ең Жоғарғы балл
О14	Квадрат үшмүшеден квадрат екімүше дұрыс айырып алынған	1	4
	Екімүшенің ең кіші мәні дұрыс табылған	1
	Функцияның ең кіші мәні дұрыс бағаланған	1
	Дұрыс жауабы алынған	1
О15	Тригонометриялық формулаларды қолданып қажетті түрлендірулер жасалды	1	4
	Аралық мәндері дұрыс табылды	1
	Қарапайым тригонометриялық теңдеу дұрыс шешілді	1
	Түбірлерді іріктеу негізделіп көрсетілген	1
О16	Берілген векторлардың абсолют шамалары дұрыс табылды	1	4
	Векторлардың скаляр көбейтіндісі дұрыс есептелді	1
	Берілген векторлар арасындағы бұрыштың косинусы дұрыс анықталған	1
	Берілген векторлар арасындағы бұрыш дұрыс анықталған	1
О17	Бірінші теңсіздік дұрыс шешілген және дұрыс жауап алынған	1	4
	Берілген теңсіздікті шешуге қажетті шарттар жазылған	1
	Табылған аралықтардың шеткі нүктелеріндегі мәндерді салыстыру жүргізілді.	1
	Дұрыс жауабы алынған	1
О18	Есеп шарты дұрыс жазылған және шарт бойынша чертеж дұрыс салынған	1	4
	Аралық элементтері дұрыс табылған (ізделінді элементті табуға қажетті қосымша элементтер).	1
	Шешу кезеңдері тізбектей және сауатты негізделген.	1
	Дұрыс жауап негізделіп алынған	1

2. – Бөлім

Ж19. а параметрінің қандай мәнінде 4^х – (2а + 7)∙14^х + 2а∙7^2х+1 = 0 теңдеуінің тек бір ғана түбірі болады?

Шешуі. Берілген теңдеуді түрлендіреміз:

4^х – (2а + 7)∙14^х + 2а∙7^2х+1 = 0 .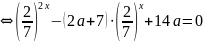

болсын, онда: t² – (2а + 7)∙t + 14а = 0 (1).

Бірінші жағдайда 4а² – 28а + 49 = 0 (2а – 7)² = 0

а = 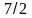; t = 7 > 0. Екінші жағдайда функция ретінде қарастырамыз f(t) = t² – (2а + 7)∙t + 14а, t₁ ≤ 0 ≤ t₂. Ол үшін келесі теңсіздікті шешеміз: f(0) ≤ 0 a ≤ 0. Сонымен,

а .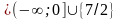

Жауабы: а .

***

Ж20. Геометриялық прогрессияның барлық мүшелері, 210 мен 350 сандарының арасында жататын, әр түрлі натурал сандар. 

а) осындай прогрессияның төрт мүшесі болуы мүмкін бе?  б) осындай прогрессияның бес мүшесі болуы мүмкін бе? 

Шешуі:

а) Төрт мүшесі бар геометриялық прогресияға мысал келтірейік

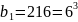
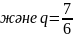
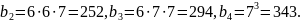
б) Есеп шартын қанағаттандыратын, бес мүшесі бар геометриялық прогрессияның табылмайтынын дәлелдейік. Ол үшін, керісінше, осындай тізбек бар деп жориық. Оның еселігі болсын, мұндағы өзара жай натурал сандар. Онда

.

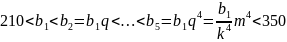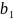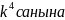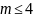
өзара жай сандар болғандықтан, саны бөлінеді, демек болғандықтан. Бірақ k бүтін сан, сондықтан

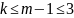
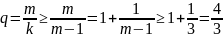
Сондықтан 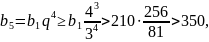бұл есеп шартына қарсы. Біз қарама-қайшылыққа келдік.

Жауабы: а) ия; б) жоқ.