5.Фурмулировка задачи оптимизации на примере проектирование бака и в общем виде:

Для успешного решения оптимизационной задачи с помощью ЭВМ необходимо знать что такое матмодель и каким образом ЭВМ находит различные варианты решения. Это – одна из задач данного курса.

Составление алгоритма. В настоящее время большинство оптимизационных расчетов выполняются с помощью коммерческих программных продуктов, о применяемых алгоритмах можно только догадываться. Частично понять какой алгоритм используется можно по исходным данным, которые требуется ввести для расчета.

Далее рассмотрим решение простейшей оптимизационной задачи.

Необходимо спроектировать бак из листовой стали в виде прямоугольного параллелипипеда объемом 2000 л.

Рассмотрим различные методы расчета бака. Объем бака:

(1)

a,b – длина и ширина основания;

h – высота бака.

Таким образом, размеры a,b и h являются искомыми параметрами.

При поверочном расчете мы задаемся некоторыми тройками значений параметров a,b,h и проверяем равняется ли их произведение заданному значению. Такой метод расчета иногда называют методом проб и ошибок.

При проектировочном расчете мы находим зависимость искомых параметров от заданных. Для нашего случая эта зависимость будет выглядеть следующим образом:

(2)

При заданном значении V, задаваясь различными парами значений a и b будем получать различные варианты бака. При этом все варианты будут заданного объема. Такой расчет называют также многовариантным. Рассмотрим три варианта (табл.1., рис.2.).

Табл.1.

Вариант	a, дм	b, дм	h, дм
1	10	5	40
2	10	20	10
3	10	35	5.7

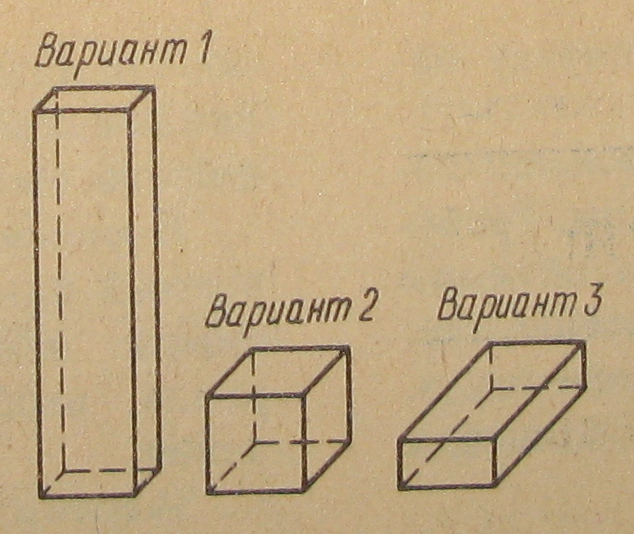
Рис.2.

Возникает вопрос: какой вариант бака выбрать? Во всех вариантах V=2000 л.

Для осуществления осознанного выбора необходимо договориться о том, по какому признаку будет выбираться наилучший вариант.

Рис.3.

Т.к. бак изготавливается из листовой стали (раскраивается, сгибается и сваривается) логичным будет при сравнении вариантов рассмотреть две величины: площадь поверхности бака S, которая определяет расход листа и длину сварного шва l (рис.3), которая, характеризует трудоемкость сварочных работ.

; (3)

; (4)

Для трех рассматриваемых вариантов значения этих величин приведены в таблице 2.

Таблица 2.

Вариант	S, мм2	l, мм
1	1300	80
2	1000	110
3	1213	166

Выводы:

1. Наилучшим в смысле минимального расхода листа является вариант №2.

2. Наилучшим в смысле минимальной длины сварного шва является вариант №3.

Возникает еще один вопрос: являются ли данные варианты абсолютно лучшими из всех возможных? Неизвестно.

Наилучший из всех возможных вариант может быть найден только после рассмотрения математической модели бака и решения задачи оптимизации.

Сформулируем задачу оптимизации следующим образом (дадим содержательную постановку):

Вариант 1: Найти размеры сторон бака объемом 2000 л так, чтобы на его изготовление требовалось как можно меньше стального листа. Такая постановка может быть записана следующим образом:

(5)

(минимизировать S при условии V=2000 л)

После подстановки выражений для S и V, получим:

(6)

К этим зависимостям необходимо добавить сл. условие, очевидное для нас, но неочевидное для ЭВМ:

(7)

Тогда мы получим математическую модель данной задачи:

(8)

Модель включает три составляющих: целевую функцию (ЦФ); ограничение (ОГР) и граничное условие (ГРУ).

ГРУ – это предельно допустимые значения переменных (параметров).

ОГР – это зависимость между искомыми переменными.

ЦФ – показывает в каком смысле решение должно быть наилучшим.

Вариант 2: Найти размеры сторон сварного бака объемом 2000 л, так чтобы длина сварного шва была минимальной.

Математическая модель для второго варианта содержательной постановки задачи будет выглядеть следующим образом:

(9)

После решения обеих оптимизационных задач на ЭВМ были получены следующие результаты (табл. 3.).

Таблица 3.

ЦФ	a, дм	b, дм	h, дм	S, дм2	l, дм
	12,6	12,6	12,6	953	88
	12,6	6,3	25,2	1111	76

Если сопоставить эти значения с найденными в результате многовариантного проектирования можно увидеть, что оптимальные значения ниже вариантных на 4%..6%. Эти значения математически обоснованы. Однако, снова видим, что решение может быть оптимальным только в одном строго определенном смысле.

Постановка задачи оптимизации в общем виде.

Для перехода к математической модели задачи оптимизации общего вида, отталкиваясь от рассмотренной ранее формулировки задачи в варианте 1, сменим в ней имена параметров: a на x₁; b на x₂;h на x₃. Во-вторых, преобразуем ограничение к виду с нулевой правой частью, т.е. сделаем его однородным. В результате приведем матмодель к следующему виду:

(10)

В реальных задачах оптимизации число переменных может быть достаточно большим. Также большим может быть и число зависимостей (ограничений) между переменными.

Обозначим переменные через x_j, j – порядковый номер переменной, j=1..n; n – общее число переменных в задаче.

Ограничения будем записывать следующим образом: g_i(x_j)=0, i – порядковый номер ограничения, i=1..m; m – общее число ограничений в задаче.

Нижнее и верхнее предельно допустимые значения переменной x_j будем обозначать a_j и b_j соответственно.

Тогда общая формулировка математической модели для решения оптимизационной задачи будет выглядеть так:

(11)

Данную модель записывают более компактно:

(12)

Рассмотрим некоторые важные частные случаи.

1. На переменные может не накладываться никаких ограничений и граничных условий. Т.е.:

и i=0.

В этом случае оптимизация называется безусловной. В реальной практике задачи безусловной оптимизации встречаются редко. Часто в технических и экономических расчетах переменные должны быть положительными. В этом случае ГРУ выглядит следующим образом:

2. В некоторых случаях задается одно конкретное значение величины x_j. Т.е. x_j = x_зад.

ГРУ в этом случае записывается так:

Ограничения могут быть теоретическими и статистическими. Статистические ограничения получают путем статистической обработки опытных данных.

Множество значений переменных x_j, удовлетворяющее всем ограничениям и граничным условиям называется областью допустимых значений. В случае решения задачи однопараметрической оптимизации (n=1), ОДР имеет вид отрезка на числовой оси. При наличии двух параметров ОДР – плоская фигура, либо кривая. При трех параметрах, ОДР может иметь вид объемной фигуры, трехмерной поверхности или кривой.

Случается, что в задачу включают требования, которые оказываются противоречивыми и выполнить которые не представляется возможным. Такие задачи называются несовместными или несбалансированными. ОДР таких задач – пустое множество. (пример с баком a,b,h<10 дм)

Для того, чтобы задача имела оптимальное решение необходимо выполнение двух требований:

- должна быть реальная возможность иметь более одного решения (ОДР – непустое множество);

- должен быть принят критерий, показывающий в каком смысле решение будет наилучшим или оптимальным (должна быть определена ЦФ).

Это есть условия разрешимости задачи оптимизации.