1.Задача оптимального проектирования:
Целью инженерной деятельности является создание «наилучших» конструкций либо способов производства изделий (в пер. на лат. наилучший – optimus). При проектировании объективно может существовать одна из двух задач:
- спроектировать изделие с заданными свойствами при минимальной себестоимости;
- спроектировать изделие заданной стоимости с максимальными свойствами.
Часто такие задачи называют задачами принятия решений.
Есть несколько способов решения этих задач:
Следование определенным нормативам и стандартам (ГОСТ, СТП, руководящие материалы и т.д.), в которых заложен опыт предыдущих поколений.
Использование инженерной интуиции, практических навыков, опыта предыдущих разработок.
Использование алгоритмов оптимального проектирования.
Первый способ наиболее прост, но область его применения ограничена. Его нельзя использовать при проектировании принципиально новых изделий. Применение второго способа требует наличия у проектировщика большого опыта работы. Он наиболее эффективен при концептуальном проектировании новых изделий. Недостатком обоих способов является неоднозначность и субъективизм в принятии решений, а также сложность внедрения в САПР.
Третий способ базируется на применении строгого математического аппарата, он гарантирует получение абсолютно наилучшего решения (с некоторыми оговорками, о которых пойдет речь далее). Наличие большого опыта работы не является обязательным. Данный способ лучше всего подходит для реализации на ЭВМ.
2.Этапы решения оптимизационных задач на эвм:
Для решения с помощью ЭВМ, приведенная выше задача оптимального проектирования должна быть преобразована (сама по себе ЭВМ не способна отыскивать наилучшие решения, она лишь может помочь их отыскивать). Основные этапы решения оптимизационной задачи с помощью ЭВМ показаны на рис.1.
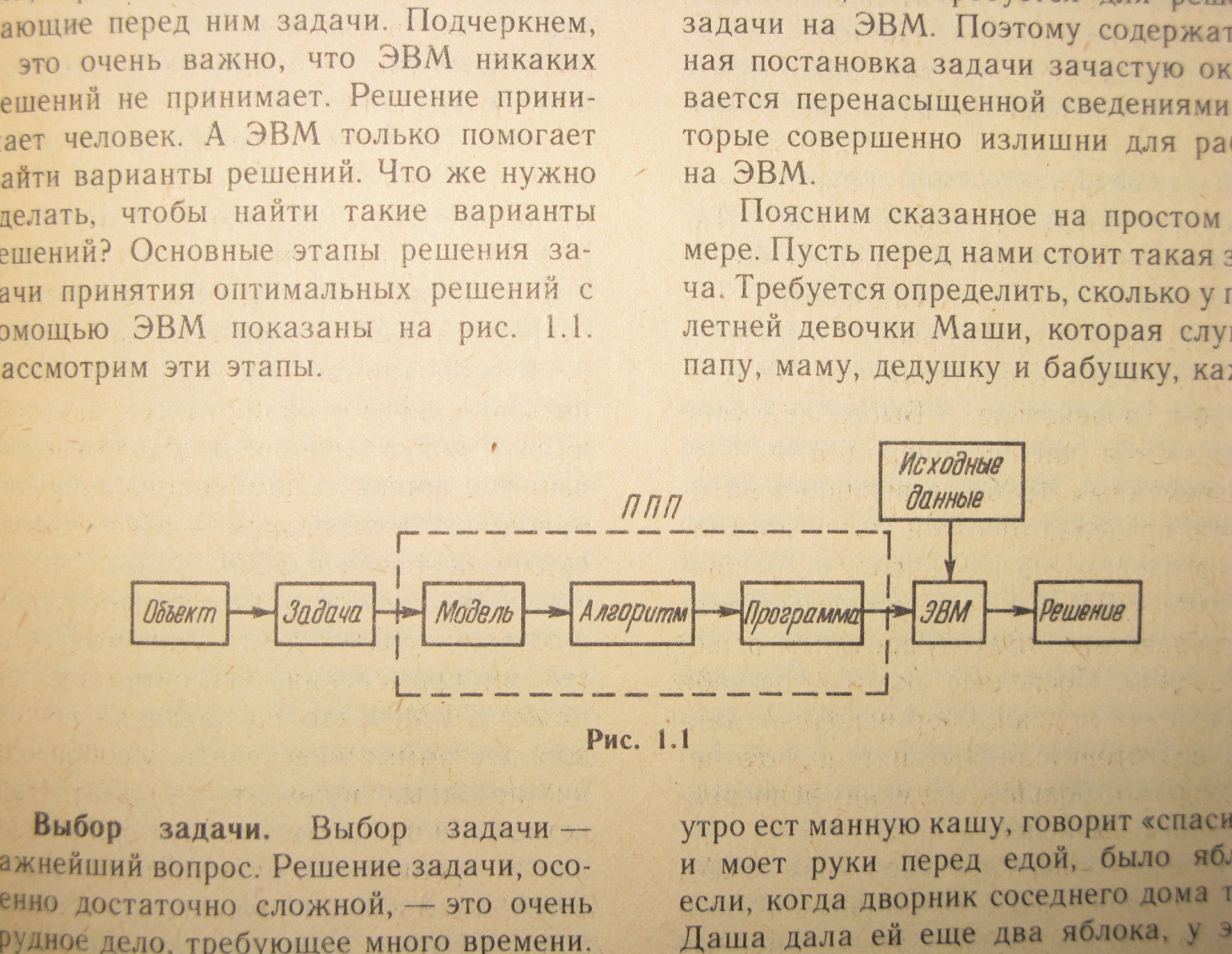
Рис.1.
3.Обьекты оптимального проектирования:
Объект проектирования (ОП) – это то, что подлежит проектированию. Объектами оптимизационного проектирования в машиностроении являются:
Технологические системы и их элементы (заводы, цеха, участки, станки (универсальные, с ЧПУ, АЛ, ГПС), а также технологическая оснастка (РИ, ВИ, приспособления).
Технологические процессы.
Физические процессы – процессы, протекающие при резании металлов в зоне резания.
Как правило, эти объекты по отдельности не рассматриваются.
Каждый ОП обладает определенными свойствами. Эти свойства могут быть количественными и качественными. Примеры количественных свойств: масса, производительность, стоимость, стойкость и др. Т.е. количественные свойства могут быть измерены в каких-то единицах.
Качественные свойства: надежность, удобство эксплуатации, качество изготовления и т.п. При решении оптимизационных задач учитываются только те свойства объектов, которые можно измерить количественно, поэтому качественные свойства необходимо оценить с помощью какого-либо количественного показателя. Например, надежность можно измерить вероятностью безотказной работы.
Количественные свойства по-другому называют параметрами. Параметры могут быть техническими (мощность, производительность), экономическими (трудоемкость, стоимость). Также параметры делят на заданные и искомые. Собственно под расчетом обычно и понимают переход от заданных параметров к искомым. Если в расчет входят только технические параметры, его называют инженерным, если наряду с техническими входят и экономические, то расчет называют технико-экономическим.