3 Конические зубчатые передачи. Основные геометрические соотношения. Эквивалентное колесо. Силы в зацеплении.

Конические зубчатые передачи передают механическую энергию между валами с пересекающимися осями. Обычно Σ = 90° (рис. 40,а). Зацепление конических зубчатых колес можно рассматривать как качение делительных круговых конусов шестерни и колеса. Основные характеристики: углы делительных конусов δ₁ и δ ₂, внешнее конусное расстояние R_e.

Линии пересечения боковых поверхностей зубьев с делительной конической поверхностью называют линиями зубьев. В зависимости от формы линии зуба различают передачи с прямыми зубьями (рис. 40,б), у которых линии зубьев проходят через вершину делительного конуса, и с круговыми зубьями (рис. 40,в), линии зубьев которых являются дугами окружности d₀.

Конические колеса с круговыми зубьями характеризуют наклоном линии зуба в среднем сечении по ширине зубчатого венца. Угол β_n наклона — острый угол между касательной в данной точке к линии зуба и образующей делительного конуса (рис. 40,в).

Разновидностью конических передач являются гипоидные передачи, у которых оси вращения зубчатых колес не пересекаются, а перекрещиваются.

Рисунок 40 –Конические зубчатые передачи

Геометрия конических зубчатых передач представлена на рис.41.

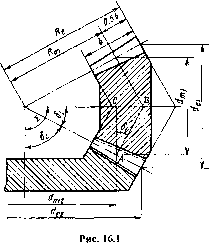
Рисунок 41 – Геометрия конических зубчатых колес

Конические зубчатые передачи необходимо регулировать, добиваясь совпадения вершин делительных конусов колес.

Угол Σ между осями зубчатых колес равен сумме углов делительных конусов (рис. 18.1):

, (61)

Достоинство конических передач – возможность передачи механической энергии между валами с пересекающимися осями.

Недостатками являются необходимость регулирования передачи (вершины делительных конусов должны совпадать), а также меньшая нагрузочная способность и большая сложность изготовления по сравнению с цилиндрическими передачами.

Внешние и внутренние торцы на конических зубчатых колесах формируют внешними и внутренними дополнительными конусами, образующие которых перпендикулярны образующей делительного конуса. Средний дополнительный конус расположен на равном расстоянии от внешнего и внутреннего дополнительных конусов.

Ширина b венца зубчатого колеса ограничена двумя дополнительными конусами – внешним и внутренним.

Длину отрезка образующей делительного конуса от его вершины до внешнего торца называют внешним конусным расстоянием R_e, до середины ширины зубчатого венца – средним конусным расстоянием R_m (рис. 41).

Пересечения делительных конусов с дополнительными конусами определяют диаметры делительных окружностей конического зубчатого колеса. Различают внешний d_e, внутренний d , средний d_m делительные диаметры.

Основные геометрические соотношения. В конических зубчатых колесах с осевыми формами I и II высота зуба, а следовательно, и модуль зацепления увеличиваются от внутреннего к внешнему дополнительному конусу (рис. 41, 42). Для удобства измерения размеры конических колес принято определять по внешнему торцу зуба.

Максимальный модуль зубьев – внешний окружной модуль т_te –получают на внешнем торце колеса.

Ниже приведены основные геометрические соотношения для конических зубчатых передач (рис. 41).

Внешнее конусное расстояние:

,

Внешние делительные диаметры шестерни и колеса:

,

Ширина зубчатого венца:

,

Для большинства конических передач коэффициент ширины зубчатого венца .

Тогда:

,

Среднее конусное расстояние:

,

Из условия подобия (рис. 18.1) следует:

,

Тогда средний делительный диаметр шестерни:

,

Модуль окружной в среднем сечении:

,

Модуль нормальный в среднем сечении для кругового зуба ( =35°):

,

Углы делительных конусов:

,

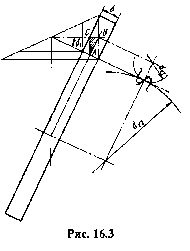
Рисунок 43 – Эквивалентное колесо

Для конических зубчатых колес с прямыми зубьями в качестве расчетного принимают внешний окружной модуль m_te, для конических зубчатых колес с круговыми зубьями – средний нормальный модуль т_п в середине зубчатого венца.

Эквивалентное колесо. Для прямозубой передачи профили зубьев конического колеса на среднем дополнительном конусе (рис. 43) близки к профилям зубьев цилиндрического прямозубого колеса с делительным диаметром d_v.

Дополнив развертку среднего дополнительного конуса на плоскость (рис. 44) до полной окружности, получим эквивалентное цилиндрическое колесо с числом зубьев и делительным диаметром:

,

Рисунок 44 – Развертка среднего дополнительного конуса на плоскость

Эквивалентного числа зубьев:

,

т.е. фактическое коническое прямозубое колесо с числом зубьев z в прочностных расчетах можно заменить цилиндрическим с числом зубьев z_v.

Для передачи с круговыми зубьями профили зубьев конического колеса в нормальном сечении близки к профилям зубьев эквивалентного цилиндрического прямозубого колеса. Эквивалентное число зубьев z_vn получают двойным приведением: конического колеса к цилиндрическому и кругового зуба к прямому зубу:

,

Силы в коническом зубчатом зацеплении. В конической передаче местом приложения силы F действующей перпендикулярно поверхности зуба, считают сечение на середине ширины зубчатого венца. Для расчета валов и опор силу F_n удобно представить в виде составляющих: F_t, F_r и F_a.

Окружная сила F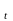 (H) на шестерне:

,

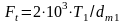где Т – вращающий момент, Н·м;

d_m – средний делительный диаметр, мм.

В прямозубой передаче (рис. 45) для определения составляющих запишем промежуточное выражение (α_w = 20° – угол зацепления)

,

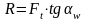Радиальная сила на шестерне:

Осевая сила на шестерне:

,

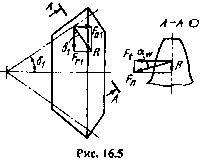
Рисунок 45 – Силы, действующие в зацеплении

Силы на колесе соответственно равны (рис. 46):

,

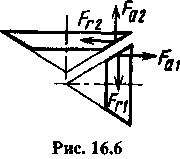
Рисунок 46 – Осевые и радиальные силы

В передаче с круговым зубом во избежание заклинивания зубьев при значительных зазорах в подшипниках необходимо обеспечить направление осевой силы F_a1 на ведущей шестерне к основанию делительного конуса. Для этого направление вращения ведущей шестерни (если смотреть со стороны вершины делительного конуса) и направление наклона зубьев должны совпадать. По рис. 47 шестерня вращается против хода часовой стрелки, т.е. влево, и зуб шестерни левый.

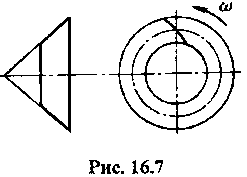
Рисунок 47 – Направление зуба шестерни

В передаче с круговым зубом при соблюдении этого условия:

радиальная сила на шестерне:

,

осевая сила на шестерне:

,

Такие же знаки в формулах будут при вращении по ходу часовой стрелки ведущей шестерни с правым зубом.

Силы на колесе соответственно равны: F_r2 = F_al; F_a2 = F_rl.