36 Система вала, система отверстия. Образование посадок в этих системах

Основное отверстие- отверстие, нижнее отклонение которого равно нулю. Основной вал - вал, верхнее отклонение которого равно нулю. Если разные посадки образованы изменением поля допуска вала при const поле допуска отверстия - система отверстия. Если за основную деталь принят вал,. а для образования разных посадок изменяют поле допуска отверстия. - система вала.

В машиностроении предпочтительнее система отверстия.

37Соотношение между силами и моментами, действующими на резьбовые детали в процессе затяжки.

Момент сопротивления в резьбе. Выявим соотношение между силой T_зат затяжки и моментом T_р сопротивления в резьбе:

,

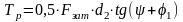Из полученной зависимости следует, что момент сопротивления в резьбе тем больше, чем больше приведенный угол трения ₁= /cos_n т.е. Т_р зависит от материала резьбовой пары и от угла  наклона рабочей стороны профиля. В метрической резьбе угол наклона профиля наибольший ( = 30°), поэтому и момент сопротивления в резьбе – наибольший. Для крепежных резьб это не является недостатком, поскольку момент сопротивления в резьбе препятствует самоотвинчиванию.

Момент Т_р сопротивления в резьбе скручивает стержень винта (создает касательные напряжения).

Момент трения на торце гайки. Контакт гайки с плоской опорной поверхностью корпуса ограничен кольцом с внутренним диаметром, равным диаметру d₀ отверстия в корпусе под стержень винта, и наружным диаметром D, соответствующим границе фаски на опорной поверхности гайки. Приближенно момент T_т трения на торце гайки определяют как произведение силы трения F_тр=F_затf_т на средний радиус R_cp=(d₀+D)/4 кольцевой поверхности:

,

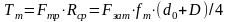Здесь f_т– коэффициент трения на поверхности контакта.

В большинстве резьбовых соединений должна быть обеспечена стабильная работа без самоотвинчивания.

Условие самоторможения резьбы без учета трения на торце гайки по аналогии с наклонной плоскостью можно записать в виде

,

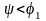где  – угол подъема резьбы (1,5...3°);

₁ – приведенный угол трения (при f=0,1...0,3 ₁=6...16°).

Отсюда следует, что все крепежные резьбы — самотормозящие. Но это только при статическом действии нагрузок. При вибрациях ₁ уменьшается вследствие микроперемещений поверхностей трения, сминания микронеровностей на рабочих поверхностях резьбы, и резьбовая пара отвинчивается. Поэтому на практике широко применяют различные способы стопорения, в которых используют:

• дополнительное трение в резьбе или на торце гайки (пружинные шайбы, контргайки, фрикционные вставки в винты или гайки);

• фиксирующие детали (шплинты, проволоку, стопорные шайбы с лапками);

• приварку или пластическое деформирование (расклепывание, кернение);

• пасты, лаки, краски, герметики и клеи.

38 Цилиндрические передачи

Цилиндрические передачи с внешним зацеплением (рис. 35). Шестерня в понижающей передаче является ведущим элементом и всем ее параметрам присваивают индекс 1. Например, частота вращения n₁, мин^–1, число зубьев z₁. Параметры ведомого элемента пары — колеса имеют индекс 2: n_2, z₂.

Линии пересечения боковых поверхностей зубьев с любой круговой цилиндрической поверхностью, соосной с начальной, называют линиями зубьев. Если линии зубьев параллельны оси зубчатого колеса, то его называют прямозубым (рис. 35,а). Если эти линии винтовые постоянного шага, то зубчатое колесо называют косозубым (рис. 35,б). С увеличением угла β наклона зуба повышается нагрузочная способность передачи, но возрастает осевая сила, действующая на валы и опоры. Обычно β = 8...18°.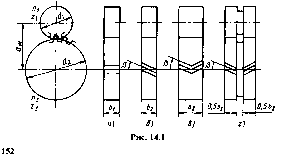

Рисунок 35 – Цилиндрические передачи с внешним зацеплением

Разновидность косозубых зубчатых колес — шевронные колеса: без канавки (рис. 35,в) и с канавкой для выхода инструмента (рис. 35,г). Вследствие противоположного направления зубьев на полушевронах осевые силы взаимно уравновешены на колесе и не нагружают опоры. Обычно β = 25...40°.

Точку W касания начальных окружностей d_w1 шестерни и d_w2 колеса называют полюсом зацепления.

Для простоты изложения будем рассматривать передачи без смещения, для зубчатых колес которых диаметры d_w начальные и d делительные совпадают: d₁ = d_w1, d₂ = d_w2. Однако в обозначении межосевого расстояния для общности изложения индекс w сохраним: a_w.

Расстояние между одноименными точками профилей соседних зубьев, измеренное в сечении, нормальном линиям зубьев, называют нормальным шагом р. Отношение р/π называют модулем:

,

Модуль является основной характеристикой размеров зубьев. Модуль измеряют в мм и назначают из стандартного ряда: ... 2; 2,5; 3; 4 ....

Запишем основные параметры зубчатой передачи через параметры зубчатых колес:

– передаточное число с учетом того, что d = mz:

,

– межосевое расстояние:

,

Значения a_w принимают из ряда предпочтительных чисел Ra40.

Обычно ширина b₂ зубчатого колеса меньше ширины шестерни. В расчетах используют отношение ψ_ba, которое называют коэффициентом ширины:

,

Значения ψ_ba стандартизованы: 0,1; 0,125; 0,16; 0,2; 0,25; 0,315; 0,4; 0,5; 0,63; 0,8. Для коробок передач с целью уменьшения размеров в направлении осей валов применяют узкие колеса ψ_ba = 0,1 – 0,2; для редукторов – широкие колеса: ψ_ba = 0,315 – 0,63.

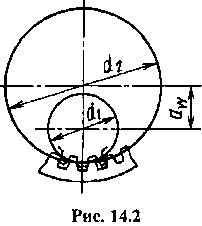
Рисунок 36 – Цилиндрическая передача с внутренним зацеплением

Цилиндрические передачи с внутренним зацеплением (рис. 36). В этом случае межосевое расстояние:

,

Силы в цилиндрическом зубчатом зацеплении. Силы взаимодействия зубьев принято определять в полюсе зацепления. Распределенную по контактной площадке нагрузку q в зацеплении заменяют равнодействующей F_n, нормальной к поверхности зуба.

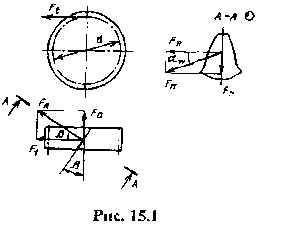
Рисунок 37 – Силы, действующие в зацеплении

Для расчета валов и опор силу F_n удобно представить в виде составляющих (рис. 37): F_t, F_a, F_r.

Окружная сила:

,

Осевая сила:

,

На ведомом колесе направление окружной силы F_t совпадает с направлением вращения, на ведущем – противоположно ему.

Осевая сила параллельна оси колеса. Направление вектора F_a зависит от направления вращения колеса и направления линии зуба.

Радиальная сила (см. сечение А–А):

,

где Т – вращающий момент на зубчатом колесе, Н·м;

d – делительный диаметр колеса, мм;

β – угол наклона зуба;

a_w = 20 ° – угол зацепления.

Векторы радиальных сил у колес с внешним зацеплением направлены к оси, а у колес с внутренним зацеплением – от оси зубчатого колеса.

Особенности геометрии и условий работы косозубых зубчатых передач. Зубья косозубых цилиндрических колес нарезают тем же инструментом, что и прямозубых. Ось червячной фрезы составляет с торцовой плоскостью колеса угол β (рис. 38). При нарезании фрезу перемещают по направлению зубьев колеса. Поэтому в нормальной к направлению зуба плоскости все его размеры – стандартные.

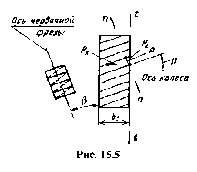
Рисунок 38 – Особенности косозубых колес

У пары сопряженных косозубых колес с внешним зацеплением углы β наклона линий зубьев равны, но противоположны по направлению. Если не предъявляют специальных требований, то колеса нарезают с правым направлением зуба, а шестерни — с левым.

У косозубого колеса (рис. 38) расстояние между зубьями можно измерить в торцовом, или окружном, (t – t) и нормальном (п – п) направлениях. В первом случае получают окружной шаг р , во втором – нормальный шаг р. Различны в этих направлениях и модули зацепления:

,

где т и т – окружной и нормальный модули зубьев.

Согласно рис. 38:

,

Следовательно:

,

где β – угол наклона зуба на делительном цилиндре.

Нормальный модуль должен соответствовать стандарту.

В торцовой плоскости t — t косозубое колесо можно рассматривать как прямозубое с модулем т, и углом зацепления :

,

Для колеса без смещения делительный d и начальный d_w диаметры

,

Помимо торцового перекрытия в косозубых передачах обеспечено и осевое перекрытие. Коэффициент осевого перекрытия:

,

где р_х – осевой шаг, равный расстоянию между одноименными точками двух смежных зубьев, измеренному в направлении оси зубчатого колеса (рис. 38).

Контактные напряжения при прочих равных условиях в косозубом зацеплении меньше по значению, чем в прямозубом.

Понятие об эквивалентном колесе. Как отмечалось, профиль косого зуба в нормальном сечении п – п (рис. 38) совпадает с профилем прямозубого колеса. Расчет косозубых колес ведут, используя параметры эквивалентного прямозубого колеса: т – модуль; z_v– число зубьев.

Профиль зуба в этом сечении совпадает с профилем условного прямозубого колеса, называемого эквивалентным, (рис. 39) делительный диаметр d_v которого d_v = m_nz_v.

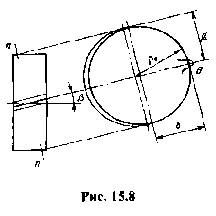
Рисунок 39 – Поперечное сечение косозубого колеса

Эквивалентное число зубьев:

, где z – действительное число зубьев косозубого колеса.

С увеличением угла β наклона линии зуба эквивалентные параметры возрастают, способствуя повышению прочности передачи.