Еквівалентні схеми пасивних двополюсників та особливості реальних пасивних елементів

Р

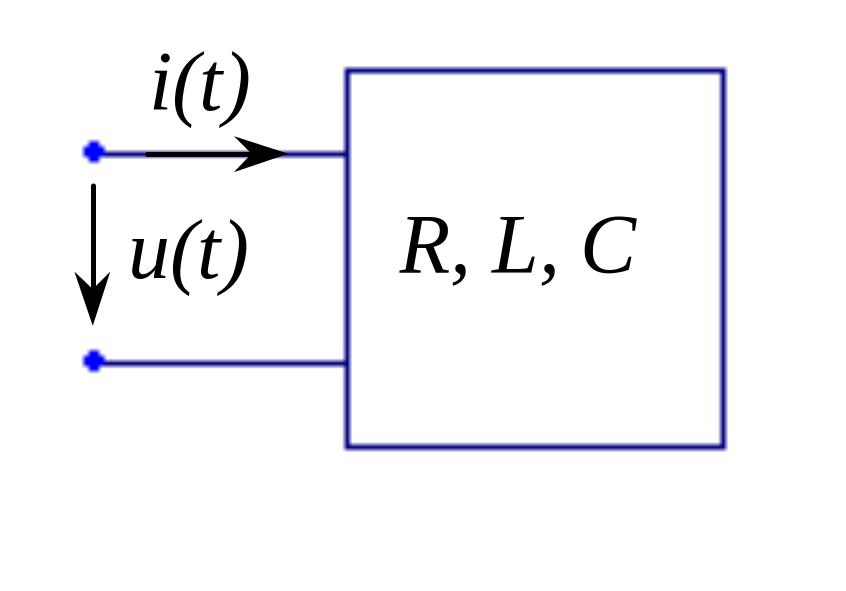
озглянемо пасивний двополюсник, до якого прикладена гармонічна напруга . У стаціонарному режимі такий двополюсник споживає струм . Відношення вимірених вольтметром та амперметром амплітудних (чи діючих) значень напруги та струму є повним опором двополюсника . Фазовий зсув між напругою та струмом можна виміряти з допомогою фазометра або осцилографа.

Аналогічна інформація міститься у комплексному опорі двополюсника

.

Д

ійсна та уявна частина комплексного опору є його активний та реактивний опори відповідно. Очевидно: , . Такі співвідношення між складовими повного опору двополюсника можна відобразити у вигляді прямокутного трикутника один із катетів якого є активний опір, інший - реактивний , а гіпотенуза якого є повний опір (рис.). Якщо то говорять, що даному двополюснику притаманний індуктивний характер. При характер буде ємнісний. Перепишемо рівняння () у формі

,

і на його основі синтезуємо коло. Легко помітити, що рівняння () відображає другий закон Кірхгофа у комплексній формі для кола з послідовно увімкненими активним та реактивним опорами. Схема кола показана на рис. і називається послідовною еквівалентною схемою пасивного двополюсника.

Інформація про відношення амплітуд напруги та струму і про їх фазовий зсув існує також у комплексній провідності

,

т

ут і - активна та реактивна складові комплексної провідності. Оскільки , то такій аналітичній залежності можна поставити у відповідність геометричне тлумачення - прямокутний трикутник з катетами рівними і та гіпотенузою (рис.). Такий трикутник називається трикутником провідностей. Якщо то говорять, що даному двополюснику притаманний індуктивний характер. При характер буде ємнісний.

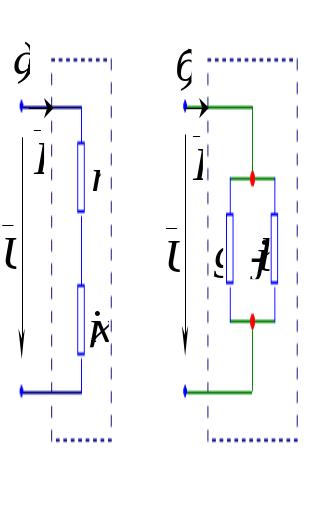
Для синтезу схеми пасивного двополюсника на основі рівняння () перепишемо його у вигляді

.

Рівняння () співпадає з рівнянням складеним за першим законом Кірхгофа для кола, схема якого показана на рис. Така схема називається паралельною еквівалентною схемою пасивного двополюсника.

Оскільки послідовна та паралельна еквівалентні схеми характеризують один і той же двополюсник , то повинен існувати зв’язок між параметрами цих схем. Установимо його.

Комплексний опір та комплексна провідність є оберненими величинами, отже

.

Позбудемося комплексності у знаменнику

.

Прирівнюючи дійсні та уявні частини у () отримаємо формули переходу від параметрів паралельної схеми до параметрів послідовної:

, .

Аналогічно можна отримати формули переходу від параметрів послідовної схеми до параметрів паралельної:

,. .

Зверніть увагу на той факт, що хоча комплексний (повний) опір та комплексна (повна) провідність обернені величини в той же час реактині та активні складові різних схем не є такими.

Енергетичні процеси в колах змінного струму.

Виникнення фазових зсувів між напругою та струмомо має істотнє значення для визначення потужності в колах змінного струму. При проходженні змінного струму по елементах електричного кола можна оцінювати як миттєве значення потужності так і середню потужність за певний проміжок часу - період для гармонічних сигналів. У стаціонарному випадку миттєве значення потужності на двополюсному пасивному елементі дорівнює добутку миттєвих значень струму та напруги на затискачах :

.

Із структури виразу () видно, що якщо різниця фаз між напругою та струмом відрізняється від нуля, то в певні проміжки часу , тобто потужність від’ємна. В ці проміжки часу струм та напруга не узгоджені за напрямком і коло енергії не споживає, а навпаки віддає накопичену енергію до джерела ЕРС. Тому для оцінки корисної роботи, яка здійснюється змінним струмом, розглядають середню потужність за період:

,

де та -діючі або ефективні значення напруги та струму. Величина називається коефіцієнтом потужності, а середнє за період значення миттєвої потужності називається активною потужністю.

Коефіцієнт потужності відіграє значну роль в електротехніці, оскільки визначає ефективність використання електроустаткування. Насправді, для отримання однієї і тієї потужності при необхідно збільшити або , або , ніж при . Проте електричні установки не в змозі витримати різниці потенціалів вищої деякого максимального значення із-за можливості електричного пробою ізоляції і не можуть пропускати струм вищий максимального допустимого із-за нагрівання провідників. Отже, при навіть при та від них не можна отримати максимально можливої потужності. Тому у будь-якій системі джерело-навантаження існує проблема , яка заключається у вимозі наближення до одиниці.

У зв’язку з цим, на генераторах змінного струму і на інших пристороях часто позначають не корисну потужність (вона залежить від якості електричного кола, тобто від величини ), а добуток , який називається позірною або повною потужністю:

.

Корисна або активна потужність, що споживається пасивним двополюсником, як було показано раніше, дорівнює

.

Якщо пасовний двополюсник є чисто резистивним елементом, то , і активна потужність завжди позитивна, тобто резистор споживає енергію:

.

В загальному випадку пасивний двополюсник можна подати у вигляді паралельної або послідовної еквівалентних схем. Розглянемо послідовну еквівалентну схему з імпедансом . Напруга на реактансі знаходиться у квадратурі із струмом , тобто , а амплітуда напруги відрізняється від амплітуди струму на множник . Отже миттєва потужність на реактивному елементі - . Із трикутника опорів для даного двополюсника випливає, що . Оскільки амплітудні значення напруги та струму на затискачах двополюсника пов’язані законом Ома - , то остаточний вираз для миттєвої потужності на реактивному елементі набуває форми:

.

Величина називається реактивною потужністю. Реактивна потужність дорівнює середньому за чверть періоду значенню енергії, якою джерело обмінюється з енергією накопиченою в магнітному полі індуктивної котушки та електричному полі конденсатора. Деякі автори для характеристики обміну енергії вводять реактивну потужність як максимальну швидкість надходження енергії в магнітне поле котушки чи електричне поле конденсатора. Реактивна потужність не перетворюється у тепло чи інші типи енергії, оскільки її середнє за період значення дорівнює нулеві.

Актвну та реактивну потужності можна виразити через параметри еквівалентних схем пасивного двополюсника :

,

.

Миттєве значення потужності на резистивному елементі еквівалентної схеми пасивного двополюсника очевидно дорівнює

.

Оскільки другий доданок у () дорівнює

,

то очевидно, що потужність , а її можна тлумачити в якості миттєвої потужності що віддається джерелом у коло, дорівнює миттєвій потужності, що споживається елементами кола, тобто

.

Вираз () відображає баланс миттєвих потужностей у колах змінного струму для конкретного випадку.

Очевидно, що усі типи потужностей мають однакову розмірність, тому для того щоб їх відрізнити від активної потужності, що вимірюється у ваттах [Вт], для повної потужності впроваджена одиниця, що називається вольт-ампери [ВА], а для реактивної потужності - вольт-ампери реактивні [ВАр].

Комплексна потужність.

Активну, реактивну та повну потужність можна визначити через комплексні амплітуди напруги та струму. Нехай , а . Тоді комплексна потужність:

,

де - комплексно спряжена амплітуда струму. Дійсна частина комплексної потужності дорівнює активній потужності, а уявна - реактивній потужності. Повна потужність - .

Комплексній потужності можна поставити у відповідність трикутник потужностей (див.рис.), який утримує інформацію про кут зсуву фаз між напругою та струмом а також про активну, реактивну та повну потужність і подібний (в математичному розумінні) до трикутника опорів.

Баланс потужностей в колах змінного струму.

Розглянемо коло, схема якого утримує  вузлів. Нехай -й та -й вузли з’єднуються віткою з імпедансом та джерелом ЕРС комплексна амплітуда якої - . Згідно узагальненого закону Ома струм у такій вітці -

.

Помножимо ліву та праву частини () на і на величину комплексно спряжену комплексній амплітуді струму - . Враховуючи, що , отримаємо

.

Знайдемо подвійну суму

.

Після зведення подібних у другій подвійній сумі отримаємо ( оскільки - перший закон Кірхгофа для -го вузла у комплексній формі).

Отже

Розглянемо кожну із подвійних сум окремо. Оскільки , то - активна та реактивна потужність, що споживається пасивними елементами у вітці між -им та -им вузлами, а

-

сумарна активна та реактивна потужності, що споживаються усіма пасивними елементами кола.

Друга сума - сума комплексних потужностей джерел, тобто

= = ,

тут - - сумарна активна потужність джерел, а - сумарна реактивна потужність джерел.

Якщо у () замість підставимо суму і прирівняємо відповідно дійсні та уявні частини рівності, то отримаємо математичну форму балансу потужностей у колах змінно струму:

;

.

Отже, у колах з гармонічними джерелами енергії виконується баланс активних та реактивних потужностей: активна потужність що надходить у коло від джерел, дорівнює активній потужності, що споживається резистивними елементами ; рективна потужність джерел енергії дорівнює реактивній потужності яку споживають реактивні елементи кола (реактивна потужність індуктивної котушки береться до уваги із додатнім знаком, а конденсатора - з від’ємним). Отриманий результат легко узагальнити і на кола з ідеальними джерелами струму.