Метод комплексних амплітуд.

Метод векторних діаграм можна назвати геометричним методом аналізу кіл при гармонічному збудженні. Існує ще один метод, його можна назвати аналітичним. Замість того, щоб рисувати векторні діаграми, подібні до наведених на рис., скористаємося формулою Ейлера і поставимо у відповідність кожному гармонічно змінному струму вираз

,

де - величина, яка називається комплексною амплітудою струму, а - комплексно спряжена величина. Очевидно, що комплексна амплітуда струму утримує інформацію про амплітудне значення струму ( ) та йго початкову фазу ( ).

Запишемо перший закон Кірхгофа для миттєвих значень гармонічних струмів

.

Замість реальних струмів підставимо у () їх представлення ():

.

Після елементарних перетворень отримаємо

.

У останній формулі рівність нулю буде мати місце тоді і тільки тоді коли

та .

Отже, якщо виконується перший закон Кірхгофа для реальних гармонічних струмів, то він виконується і для комплексних амплітуд струмів, тобто

.

Вираз () і є першим законом Кірхгофа у комплексній формі.

Необхідно зауважити, що автоматично виконується при дотриманні умови , бо дія спряження переставна з арифметичними діями над комплексними числами, тобто .

Приклад 1.Знайдемо амлітуду струму , тобто його довжину , та початкову фазу у прикладі наведеному на початку попереднього параграфу. Перший закон Кірхгофа для згаданого вузла у комплексній формі

Довжина комплексного числа у квадраті, є саме комплексне число помножене на спряжене йому:

Оскільки , то остаточний результат буде наступним

.

Для знаходження початкової фази скористаємося (), і згадаємо, що два комплексні числа рівні тоді і тільки тоді коли рівні окремо їх дійсні та уявні частини:

;

.

Звідки , або

.

З допомогою тригонометрії та рис. легко переконатися у справедливості отриманих результатів.

За аналогією, можна показати, другий закон Кірхгофа у комплексній формі має має вигляд

,

де та - комплексні амплітуди спаду напруги на пасивних елементах кола та параметрів джерел е.р.с. відповідно.

Проте у такій формі закони Кірхгофа () та () не дозволяють скласти систему рівнянь для знаходження струмів у вітках.. Щоб замкнути рівняння () та () у метод рівняннь Кірхгофа підключимо компонентні рівняння для пасивних елементів:

, , .

Якщо у колі має місце стаціонарний режим при гармонічному збудженні, то напруги на пасивних елементах та струми, які течуть крізь них також змінюються за гармонічним законом. Тоді

,

.

Тут - символи , та . Підставимо () та () з відовідними індексами у компонентні рівняння ():

,

,

.

Звідки

, , .

Співвідношення () можна тлумачити як компонентні рівняння у комплексній формі, якщо пасивним елементам приписати параметри :

, , .

Отже резистор в колах гармонічного струму характеризують опором . Параметри індуктивної котушки та конденсатора чисто реактивні і називаються реактансами; вони вносять у коло не тільки ефективний опір а і зсув за фазою.

Якщо до послідовно увімкнених резистора, індуктивної котушки та конденсатора прикладена гармонічна напруга частоти , то рівняння складене за другис законом Кірхгофа має вигляд

.

Шляхом схожих перетворень можна отримати для даного кола закон Ома у комплексній формі:

,

де - комплексний опір або імпеданс кола. Неважко переконатися у тому, що .

Таким чином імпеданс послідовно увімкнених елементів можна отримати із опору та реактансів окремих елементів за звичними формулами послідовного з’єднання.

При паралельному з’єднанні резистора, індуктивної котушки та конденсатора закон Ома у комплексній формі записують так:

,

де - комплексна провідність, причому .

Отже комплексну провідність паралельно увімкнених елементів знаходять з використанням формул для паралельного з’єднання.

Таким чином, символічне зображення опорів склад-них кіл можна отримати із зображень опорів окремих ві-ток за звичними формулами послідовного та паралель-ного, сполучень.

На рис. підбиті підсумки наших міркувань стосовно трьох пасивних елементів кола - індуктивної котушки, конденсатора, резистора - у символічному методі. На цьому рисунку комплексна амплітуда напруги помічена стрілкою, направленою від одного затискача до іншого.

Приклад 2. Знайти еквівалентний опір складного кола, схема якого показана на рис., якщо: Ом, Ом, Ом, Ом.

О

скільки нам відомі прийоми заміни простих послідовних та паралельних сполучень резисторів, то запропоновану схему можна спростити, якщо скористатися символічними зображеннями конденсаторів та методом еквівалентних перетворень. Перш за все замінимо послідовне сполучення та еквівалентним імпедансом : . Потім знаходимо еквівалент-ний імпеданс послідовно з’єднаних та : . Таким чином ми отрима-ли більш просту еквівалентну схему (рис.), у якій не виникає складнощів для знаходження , яке вияв-ляється буде дорівнювати імпедансу кола, що складається з паралельно з’єднаних та :

.

Підставимо значення параметрів елементів та їх символічних зображень, і, остаточно знайдемо

Ом.

Таким чином, при складанні системи рівнянь по методу рівнянь Кірхгофа, всі дії здійснюються над імпедансами пасивних елементів та комплексними амплітудами за звичними формулами аналізу кіл при постійному струмі. При цьому рівняння Кірхгофа набувають алгебраїчної форми

, .

В результаті розв’язку системи рівнянь складених за методом Кірхгофа отримаємо комплексні амплітуди струмів у вітках. Як перейти до реальних струмів? Необхідно комплексну амплітуду струму домножити на множник обертання і від добутку утворити комплекно спряжену величину. Якщо збудження здійснюється за законом косинуса то реальний струм у вітці - ; якщо за законом синуса, то - . Проте на практиці, формально, в залежності від типу збудження виділяють уявну чи дійсну частину від добутку комплексної амплітуди на множник обертання, тобто

, або .

Якщо параметри елементів електричного кола відомі, то імпеданси для усіх віток можна знайти вище згаданим способом . Тоді, при гармонічному збудженні, у рівняння () необхідно підставити комплексні аиплітуд параметрів джерел і розв’язати систему рівнянь відносно комплексних амплітуд струмів у вітках. Потім отримані комплексні амплітуди струмів помножити на множник обертання і від результату взяти дійсні чи уявні частини, саме ті, які були в початковому представлені.

П

риклад. У колі, схема якого показана на рис, діє ідеальне джерело ерс миттєве значення якої В. Знайти струми у вітках якщо: Ом, Ом, Ом, мГн, мГн, мкФ.

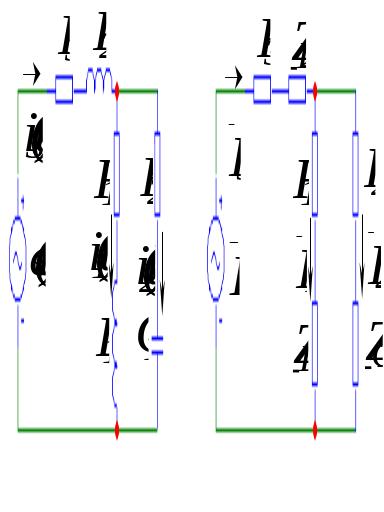
Рішення. Скористаємося методом рівнянь Кірхгофа у символічній формі. Знайдемо реактанси символічних зображень пасивних елементів кола. Симолічні зображення відрізняються від реальних тільки для індуктивних котушок та конденсатора і в нашій задачі будуть такими:

Ом; Ом;

Ом.

Комплексна амплітуда джерела гармонічної ЕРС - .

Перейдемо від схеми реального кола до схеми символічного (див. рис.) і для останнього запишемо систему рівнянь Кірхгофа у комплексній формі (змінними у цій системі будуть комплексні амплітуди струмів у вітках - , та ):

.

Розв’язуючи цю систему, отримаємо

;

; .

Для того, щоб перейти до реальних струмів у вітках

1. представимо комплексні амплітуди струмів у показниковій формі:

, , ;

2. Помножимо комплексні амплітуди струмів на множник обертання і від отриманих виразів виділимо уявну частину: А, А,

А.

Оскільки система рівнянь (), складених на основі законів Кірхгофа, лінійна, то для знаходження значень комплексних амплітуд струмів та напруг можна користуватися принципом суперпозиції, методом контурних струмів, методом вузлових потенціалів, методом еквівалентного генератора. При цьому елементи матриці у методі контурних струмів чи вузлових потенціалів будуть комплексними. Отже метод комплексних амплітуд дозволяє поширити на аналіз кіл при гармонічному збудженні всі відомі методи та прийоми розрахунку складних кіл в режимі постійного струму.

Простота дослідження стаціонарного режиму при гармонічному збуджені методом комплексних амплітуд поєднує переваги аналітичних методів із наочністю векторних побудов. Слід підкреслити, що у методі комплексних амплітуд векторна діаграма не є безпосереднім засобом розрахунку, а може бути використана для контролю вірності отриманих результатів. Подальше викладення курсу здійснюється із застосуванням методу комплексних амплітуд. Економія в обчисленнях при цьому відчутна.

Для іллюстації аналітичного методу розглянемо декілька прикладів.