РАЗДЕЛ 6. МАШИНЫ ДЛЯ СЖАТИЯ И ПЕРЕМЕЩЕНИЯ ГАЗОВ. ХАРАКТЕРИСТИКИ КОМПРЕССОРОВ И МЕТОДЫ ИХ РЕГУЛИРОВАНИЯ

ЛЕКЦИЯ 11. ТЕХНИЧЕСКИЕ ПАРАМЕТРЫ ЦЕНТРОБЕЖНЫХ КОМПРЕССОРОВ. ОСНОВЫ ТЕРМОДИНАМИКИ ЦЕНТРОБЕЖНЫХ КОМПРЕССОРОВ

Центробежный компрессор ЦБК и центробежный насос ЦБН относятся к одному классу динамических машин. Принцип действия их одинаков, они также имеют, как это следует из предыдущего параграфа, конструктивное сходство. Уравнение Эйлера, используемое для ЦБН, применяется также для компрессоров. Для них также можно записать выражение теоретического напора. Используя теорему об изменении момента количества движения, можно записать

Н_Т = k·Н_Т∞, (5.1)

где k - поправочный коэффициент на конечное число лопаток, зависящий от кинематики и конструктивных параметров компрессора (находится в пределах 0,5..0,9);

(5.2)

Коэффициент k в теории ЦБК называют также коэффициентом циркуляции. В реальных колесах компрессоров Z = 20…30, в колесах ЦБН обычно Z = 4…8. В случае отсутствия закрутки на входе α₁ = 90⁰, cos α₁ = 0 и выражение (5.2) упрощается.

Рисунок 5.1

С₂ - вектор абсолютной скорости на выходе из колеса;

W₂ - вектор относительной скорости на выходе из колеса;

U₂ - окружная скорость вращения колеса при радиусе его на выходе r₂;

С_2r - радиальная скорость на выходе из колеса.

Угол β₂ = 30…60⁰ (он обычно больше, чем в ЦБН, что приводит к увеличению напора). Радиальную скорость V_2r легко связать с подачей колеса Q₂, что видно из рис 5.2.

, (5.3)

где S₂ - площадь выхода потока из колеса с учетом коэффициента стеснения потока (≈0,95). Из треугольника скоростей (рис. 5.1) можно также записать

.

Подставляя это выражение в (2) с учетом (1) и (3) получим

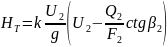. (5.4)

Это выражение связывает теоретический напор компрессора с его подачей на выходе из колеса.

В формуле (5.4) под Н_Т понимается величина энергии А, передаваемая единице веса газа, как это принято в гидравлике.

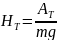. (5.5)

Рисунок 5.2

В термодинамике удельную энергию принято относить к единице массы (l_Т). Это понятие ниже будет использоваться в термодинамических задачах.

. (5.6)

Связывая массовую подачу компрессора Q_m с объемной, получим

, (5.7)

где v₂ – удельный объем газа на выходе из компрессора.

Используя (5.5) и (5.6), выражения (5.2) и (5.4) представляем в виде

, (5.8)

, (5.9)

где

.

Нетрудно установить, что

. (5.10)

Запишем еще известное соотношение между приростом давления в колесе и удельной работой:

. (5.11)

Анализ уравнения (5.11) показывает, что в отличие от ЦБН в ЦБК для получения такого же перепада давления необходимо затратить значительно большую удельную работу. Это объясняется меньшими значениями ρ_г по сравнению с плотностью жидкости (примерно на три порядка).

Чтобы выяснить технические пути этого увеличения 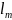, рассмотрим выражение (5.9).

Для данной конструкции компрессора (k, F₂, β₂) и заданной массовой подачи М мы имеем единственное решение - значительное увеличение окружной скорости U₂ = ω·R₂. Иначе говоря, компрессоры по сравнению с ЦБН должны иметь значительно большую угловую скорость вращения и диаметр рабочего колеса. Обычно число оборотов вала ЦБК, которые применяются в нефтяной промышленности, находятся в пределах 4000... 12000 об/мин, а диаметр колеса достигает 0,9 м. Линейные скорости вращения U₂ достигают при этом 300 и более м/с, того же примерно порядка будут и абсолютные скорости движения газа. Это обстоятельство требует при энергетических расчетах ЦБК учитывать удельную кинетическую энергию газа .

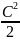Сечение канала рабочего колеса ЦБК сужается к периферии. Это объясняется уменьшением удельного объема v₂ по мере роста давления при движении газа к выходу, а, следовательно, и объемной подачи (5.7). Массовая подача вдоль проточной части компрессора не меняется. Таким образом, имея аналогию ЦБК и ЦБН, мы усматриваем в них принципиальные кинематические и конструктивные различия.

Большие скорости газа могут вызвать в ЦБК критические и закритические (сверхзвуковые) режимы, что требует особого подхода к их гидродинамическим расчетам.

Основы термодинамики центробежных компрессоров

В предыдущем разделе мы рассмотрели работу компрессора с точки зрения закона сохранения механической энергии (законов гидродинамики). Анализ работы компрессора можно выполнить также, применяя законы термодинамики. Поскольку состояние газа определяется тремя параметрами (Р, v, Т), к нему удобно применить первое начало термодинамики. Для открытых систем с большой кинетической энергией его можно записать в следующей дифференциальной форме (перемещение на расстояние dx):

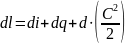, (5.12)

где l - подводимая к газу удельная работа. Она близка к значению внутренней работы l_i = gH_i, будучи меньше ее на величину работы утечек (Δl_У). В уравнении (13) рассматривается неизменное количество массы газа:

i = U + p·v. (5.13)

Это функция энтальпии газа, зависящая от его внутренней энергии U и величины pv.

Для совершенных газов

di = C_p·d·T. (5.14)

Величина q – теплота, подводимая или отводимая от компрессора. Она определяется через энтропию

dq = T·d·S. (5.15)

Если ввести параметры торможения газа, то величину в (5.12) можно исключить.

Для совершенного потока газа согласно законам газодинамики можно записать

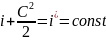
или

,

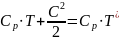откуда

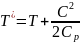. (5.16)

В этом уравнении С, Т* - скорость и температура заторможенного газа; С_р - удельная теплоемкость газа при постоянном давлении.

Используя (16), выражение (12) перепишем теперь в следующем виде:

dl = di + dq. (5.17)

Применяем для этого уравнения всюду соответствующие температуры торможения.

Уравнение (5.17) удобно проиллюстрировать в координатах Т^*-S (риунке 5.3).

На этом рисунке Р₁, Р₂ - соответствующие изобары для входа и выхода из ступени компрессора; 1:2 - политропический процесс сжатия газа от P₁ до Р₂. Приближенно обычно принимают этот процесс линейным, т.е. проходящим при постоянном значении политропы сжатия n.

Величина этого показателя для центробежных компрессоров находится в пределах 1,55…1,6.

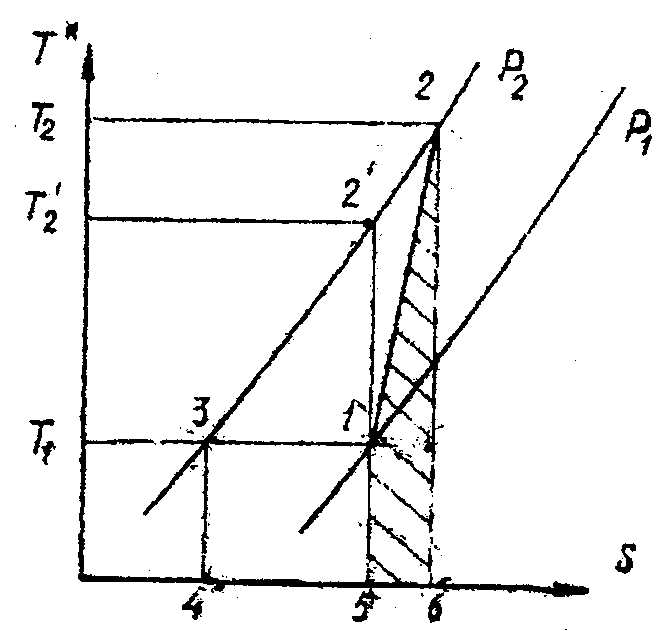
Рисунок 5.3

1:2 – адиабатический процесс сжатия.

1:3 – изотермический процесс сжатия.

Поскольку центробежные компрессоры не охлаждаемы, для них dq=0, поэтому адиабатический процесс близок к реальному. Однако фактически в процессе работы компрессора при движении газа с большими скоростями выделяется теплота трения q_тр, связанная в основном с гидравлическими и дисковыми потерями. На рис. 5.3 эта теплота заштрихована.

Затрачиваемая удельная работа компрессора 1 с учетом теплоты трения определяется площадью 4326. Ее можно подсчитать с учетом (5.14) и (5.17) по зависимости (после интегрирования)

l = C_Р·(Т₂ - Т₁). (5.18)

(Для простоты обозначения звездочка в температурах опущена). Соответственно адиабатическая удельная работа компрессора определяется площадью 432^/5 и зависимостью

l_ад = C_Р·(Т₂^/ - Т₁). (5.19)

Политропическая работа определяется площадью 43215 и равна согласно термодинамике

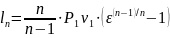. (5.20)

Тепловое совершенство центробежного компрессора оценивается с помощью политропического или адиабатического к.п.д.:

, (5.21)

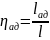. (5.22)

Подсчитаем величину политропического к.п.д., для чего выполним некоторые известные преобразования:

.

Здесь была использована зависимость

Т₂ = Т₁·ε^(n-1)/n, а также Р₁v₁ = RT₁. (5.23)

Аналогично

.

Подставляя полученное выражение в (21), имеем

. (5.24)

Показатель политропы при этом можно подсчитать, используя (5.23), если известны температуры в начале и конце сжатия.

Рассуждая аналогично, для адиабатического к.п.д. получим

. (5.25)

Величину 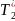найдем из (23) при n = k.

Значения η_п и η_ад весьма близки друг к другу ввиду малой степени сжатия.

В настоящее время более употребительна формула (5.24).