
- •1 Билет Кинематика поступательного движения материальной точки
- •2 Билет Динамика материальной точки. Законы Ньютона
- •3 Билет Кинематика вращательного движения
- •5 Билет Момент силы. Момент инерции. Момент импульса.
- •7 Билет: Работа силы
- •11 Билет: Принцип относительности Галилея
- •12 Билет: Основы сто. Преобразования Лоренца и следствия из них.
- •18 БилетСвязь между напряженностью и потенциалом
- •50 Билет: Ферромагнетизм. Типы ферромагнетиков и их применение
18 БилетСвязь между напряженностью и потенциалом
Из
выше сказанного следует, что электрическое
поле характеризуется двумя физическими
величинами: напряженностью (силовая
характеристика) и потенциалом
(энергетическая характеристика). Выясним
как они связаны между собой. Пусть
положительный заряд q перемещается
силой электрического поля с эквипотенциальной
поверхности, имеющей потенциал ![]() ,
на близко расположенную эквипотенциальную
поверхность, имеющую потенциал
,
на близко расположенную эквипотенциальную
поверхность, имеющую потенциал ![]() (рис.
13.16).
(рис.
13.16).

Напряженность
поля Е на всем малом пути dx можно считать
постоянной. Тогда работа перемещения ![]() С
другой стороны
С
другой стороны ![]() .
Из этих уравнений получаем
.
Из этих уравнений получаем
|
(13.22) |
Знак минус обусловлен тем, что напряженность поля направлена в сторону убывания потенциала, тогда как градиент потенциала направлен в сторону возрастания потенциала.
19 билет: Дипольный момент.
ДИПОЛЬНЫЙ
МОМЕНТ электрический,
векторная величина, характеризующая
асимметрию распределения положит. и
отрицат. зарядов в электрически
нейтральной системе. Два одинаковых
по величине заряда +q и —q образуют
электрич. диполь с дипольным моментом =
q l, где l - расстояние между зарядами.
Для системы из п зарядов qi радиусы-векторы
к-рых ri, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Поведение вещества в электрическом поле определяется основными электрическими характеристиками молекул — постоянным дипольным моментом и поляризуемостью. Дипольный момент означает несовпадение «центров тяжести» положительных и отрицательных зарядов в молекуле (электрическую асимметрию молекулы). То есть молекулы, имеющие центр симметрии, например H2, лишены постоянного дипольного момента, и наоборот. Поляризуемость — это способность электронной оболочки любой молекулы перемещаться под действием электрического поля, в результате чего в молекуле образуется наведенный дипольный момент. Значение дипольного момента и поляризуемости находят экспериментально с помощью измерения диэлектрической проницаемости. Оптические свойства вещества характеризуют его поведение в переменном электрическом поле световой волны и определяются поляризуемостью молекулы этого вещества. С поляризуемостью непосредственно связаны преломление и рассеяние света, оптическая активность и другие явления, изучаемые молекулярной оптикой.
20 билет: виды поляризации. Вектор поляризации. Начало формы
Электронная поляризация - смещение электронного облака относительно центра ядра атома или иона в результате чего возникает электрический момент, исчезающий после окончания действия электрического поля. Наблюдается во всех без исключения диэлектриках. Единственным видом поляризации она является в неполярных диэлектриках. Время протекания поляризации 10-14 - 10-15с. Так как после снятия поля деформированные электронные оболочки возвращаются прежнее положение, то энергия, затраченная на поляризацию, возвращается источнику электрической энергии, поэтому эта поляризация происходит без потерь энергии. Электронная поляризация вместе ионной составляют группу "упругих" или быстрых видов поляризаций. Ионная поляризация - наблюдается в веществах с ионной химической связью и проявляется в смещении друг относительно друга разноименно заряженных ионов. Как указывалось, время электронной поляризации весьма мало - на 2 - 3 порядка больше ионной поляризации. Релаксационные (замедленные) виды поляризации - проявляются в газах, жидкостях и твердых диэлектриках в том случае, если они состоят из полярных молекул, диполей или молекул, имеющих отдельные радикалы или части (сегменты), обладающие собственными электрическими моментами: дипольная; дипольно - релаксационная; дипольно - радикальная. В твердых телах возможны также различные разновидности релаксационных поляризаций, связанные, главным образом, с химическим составом, структурой и типом дефектов поляризации: электронно - релаксационная; ионно - релаксационная; миграционная; спонтанная. Дипольную поляризацию часто называют ориентационной, так как она проявляется в появлении некоторой упорядоченности в расположении полярных молекул, совершающих хаотические "тепловые" движения под действием электрического поля. При дипольно-радикальной или дипольно-сегментальной поляризации в некоторых полярных полимерах под действием поля происходит определенное упорядочение полярных радикалов или более крупных частей макромолекул - сегментов. Релаксационная поляризованность при дипольно-релаксационной поляризации после приложения поля к диэлектрику нарастает во времени до установления значения Pо согласно выражению
где P(t) поляризованность в момент t, а после снятия внешнего поля уменьшается по закону
В этих выражениях - постоянная времени процесса, называется временем релаксации - она равна времени, за которое поляризация уменьшается в "е" раз, т.е. приблизительно в 2,7 раза (е - основание натурального логарифма). Для полярных диэлектриков величина поляризуемости = э + др (16) Величина дипольно-релаксационной поляризуемости определяется по формуле
где электрический дипольный момент, k постоянная Больцмана, T абсолютная температура. Зависимость диэлектрическ Ионно-релаксационная поляризация наблюдается в диэлектриках с ионным типом химических связей, например в неорганических стеклах, имеющих неплотную упаковку ионов, электротехническом фарфоре и других. Слабо связанные ионы вещества под действием приложенного электрического поля среди хаотических тепловых перебросов получают избыточные перебросы в направлении поля, и смещаются на расстояния, существенно превышающие величину смещения ионов при упругой ионной поляризации. После исчезновения внешнего поля ионы постепенно возвращаются к центрам равновесия. При этом наблюдается необратимое рассеяние энергии в виде тепла. Поляризация этого типа наблюдается при низких частотах. Миграционная поляризация наблюдается в неоднородных диэлектриках, имеющих проводящие и полупроводящие включения, слои с различной проводимостью и т.п. При внесении неоднородных диэлектриков в электрическое поле свободные заряды смещаются и концентрируются на граничных слоях включений, в приэлектродных слоях и т.д., образуя пространственные заряды, поле которых внешне проявляет себя как"дополнительный" механизм поляризации. Для устранения миграционной поляризации и создания материала с небольшими потерями необходимо избавиться от пор, механических включений и примесей, прежде всего обладающих большой подвижностью ионов Li+, Na+, K+. При наличии миграционной поляризации диэлектрическая проницаемость диэлектриков на низких частотах, имеющая повышенные значения, с увеличением частоты резко уменьшается по закону, близкому к гиперболическому. Электронно-релаксационная поляризация характерна для твердых диэлектриков, содержащих дефекты или примесные ионы, способные захватывать электроны. Такие захваченные на "ловушках" электроны или дырки при отсутствии электрического поля могут под действием тепловых флуктуаций переходить из одного вероятного положения в другое. При этом суммарный электрический момент единицы объема диэлектрика будет равен нулю. Во внешнем электрическом поле такие переходы будут осуществляться преимущественно в направлении поля и в объеме диэлектрика индуцируется электрический дипольный момент, т.е. будет происходить поляризация. Время релаксации данного механизма поляризации при комнатной температуре 10-2 - 10-7с. Этот вид поляризации существенную роль играет в поликристаллической керамике типа рутила TiO2, перовскита CaTiO3, в керамических материалах, изготовленных на основе сложных оксидов титана, циркония, ниобия, тантала, свинца, церия, висмута, имеющих важное техническое значение. Наиболее вероятный механизм возникновения тепловой электронной поляризации в этих веществах связан с возникновением анионных вакансий, возникающих в процессе высокотемпературного синтеза, при котором часть ионов кислорода покидает свои места. Кислородные вакансии являются эквивалентными положительными зарядами, вблизи которых для их компенсации в соответствии с принципом электронейтральности локализуются квазисвободные электроны, которые и обусловливают тепловую электронную поляризацию. Электронно-релаксационная поляризация играет существенную роль на низких частотах в люминесцирующих широкозонных и оксидных полупроводниках. В некоторых классах полярных ионных кристаллов и веществах, относящихся к группе жидкокристаллических, в определенном температурном интервале наблюдаются фазовые переходы без изменения агрегатного состояния, в процессе которых происходит существенная перестройка их структуры. Такая перестройка не нарушая физически и химически однородное состояние вещества, приводит к существенному изменению электрических свойств диэлектриков (проводимости, диэлектрической проницаемости), оптической активности и др. Вблизи фазовых переходов, возникающих при изменении параметров окружающей среды, данные параметры могут изменяться резко, иногда на несколько порядков по величине. Такие фазовые переходы, при которых неполярные вещества самопроизвольно (спонтанно) переходят в полярное состояние называют сегнетоэлектрическими, а сам процесс перехода в новое состояние спонтанной поляризацией. Неполярная фаза, как правило, является более высокотемпературной, чем полярная, но в каждом сегнетоэлектрическом веществе фазовые переходы имеют свои особенности. Для сегнетоэлектриков характерны зависимости диэлектрической проницаемости от температуры с резко выраженным максимумом, который наблюдается вблизи точки перехода (точки Кюри Тк).
21билет: Теорема О-Г для диэлектрика Для поля в диэлектрической среде электростатическая теорема Гаусса может быть записана еще и иначе (альтернативным образом) — через поток вектора электрического смещения (электрической индукции). При этом формулировка теоремы выглядит следующим образом: поток вектора электрического смещения через замкнутую поверхность пропорционален заключённому внутри этой поверхности свободному электрическому заряду:
В дифференциальной форме:
Важно понимать, что Q и ρ в этом параграфе обозначены другие величины, чем в предыдущем: величина свободныхзарядов и плотность свободных зарядов, то есть зарядов за исключением индуцируемых при поляризации диэлектрической среды (тогда как в предыдущем параграфе имелись в виду полный заряд и полная плотность заряда (подробнее — см. комментрарий в этом параграфе чуть выше). Совпадают эти величины только для случая вакуума (отсутствия диэлектрической среды), когда и сами уравнения этого параграфа переходят по сути в уравнения предыдущего параграфа.
Если электрическое поле имеет место в диэлектрике, то наблюдается поляризация вещества и появляются связанные электрические заряды. Учитывают
поляризацию с помощью вектора
поляризации Кроме этого, при анализе электростатических полей используют вектор электрического смещения:
(1.8) Единицей электрического смещения является кулон на метр квадратный (Кл/м2). Величина e = e0 + c является основной характеристикой диэлектрика и называется абсолютной диэлектрической проницаемостью. Отношение er = e/e0 называют относительной диэлектрической проницаемостью.
22 билет: Вектор электрического смещения Если электрическое поле имеет место в диэлектрике, то наблюдается поляризация вещества и появляются связанные электрические заряды. Учитывают поляризацию с помощью вектора поляризации , который для анизотропных и однородных сред выражается через напряженность поля следующим образом: , где c – диэлектрическая восприимчивость вещества (диэлектрика). Вектор поляризации равен также поверхностной плотности связанных зарядов, возникающих в диэлектрике под воздействием внешнего электрического поля (Р = sсвяз ). Кроме этого, при анализе электростатических полей используют векторэлектрического смещения: . (1.8) Единицей электрического смещения является кулон на метр квадратный (Кл/м2). Величина e = e0 + c является основной характеристикой диэлектрика и называется абсолютной диэлектрической проницаемостью. Отношение er = e/e0 называют относительной диэлектрической проницаемостью.
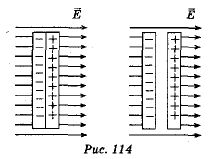
23 билет: Электростатическая индукция — явление наведения собственного электростатического поля, при действии на тело внешнего электрического поля. Явление обусловлено перераспределением зарядов внутри проводящих тел, а также поляризацией внутренних микроструктур[1] у непроводящих тел. Внешнее электрическое поле может значительно исказиться вблизи тела с индуцированным электрическим полем. Электростатическая индукция в проводниках Перераспределение зарядов в хорошо проводящих металлах при действии внешнего электрического поля происходит до тех пор, пока заряды внутри тела практически полностью не скомпенсируют внешнее электрическое поле. При этом на противоположных сторонах[2] проводящего тела появятся противоположные наведённые (индуцированные) заряды. Электростатическая индукция в диэлектриках Диэлектрики в электростатическом поле поляризуются. Применение Наиболее массовое применение находит основанная на данном явлении электростатическая защита приборов и соединительных цепей. Данный эффект используется в ряде приборов, например в генераторе Ван де Граафа. Проводники в электрическом поле Наличие свободных электрических зарядов в проводниках можно обнаружить в следующих опытах. Установим на острие металлическую трубу. Соединив проводником трубу со стержнем электрометра, убедимся в том, что труба не имеет электрического заряда. Наэлектризуем эбонитовую палочку и поднесем к одному концу трубы. Труба поворачивается на острие, притягиваясь к заряженной палочке. Следовательно, на том конце трубы, который расположен ближе к эбонитовой палочке, появился электрический заряд, противоположный по знаку заряду палочки. Если на одном конце трубы под действием электрического поля заряженной палочки появился положительный электрический заряд, то на другом конце в соответствии с законом сохранения электрического заряда должен появиться равный ему по абсолютному значению отрицательный электрический заряд.
Опыт показывает, что действительно две части металлического тела, разделенного в электрическом поле, обладают электрическими зарядами (рис. 114). Эти заряды равны по модулю и противоположны по знаку. Явление разделения разноименных зарядов в проводнике, помещенном в электрическое поле, называется электростатической индукцией. При внесении в электрическое поле тела из проводника свободные заряды в нем приходят в движение. Перераспределение зарядов вызывает изменение электрического поля. Движение зарядов прекращается только тогда, когда напряженность электрического поля в проводнике становится равной нулю. Свободные заряды перестают перемещаться вдоль поверхности проводящего тела при достижении такого распределения, при котором вектор напряженности электрического поля в любой точке перпендикулярен поверхности тела. Поэтому в электрическом поле поверхность проводящего тела любой формы является эквипотенциальной поверхностью.
24 билет: Электрическая ёмкость — характеристика проводника, мера его способности накапливать электрический заряд. В теории электрических цепей ёмкостью называют взаимную ёмкость между двумя проводниками; параметр ёмкостного элемента электрической схемы, представленного в виде двухполюсника. Такая ёмкость определяется как отношение величины электрического заряда к разности потенциаловмежду этими проводниками. В системе СИ ёмкость измеряется в фарадах. В системе СГС в сантиметрах. Для одиночного проводника ёмкость равна отношению заряда проводника к его потенциалу в предположении, что все другие проводники бесконечно удалены и что потенциал бесконечно удалённой точки принят равным нулю. В математической форме данное определение имеет вид
Ёмкость определяется геометрическими размерами и формой проводника и электрическими свойствами окружающей среды (её диэлектрической проницаемостью) и не зависит от материала проводника. К примеру, ёмкость проводящего шара радиуса R равна (в системе СИ):
где ε0 — электрическая постоянная, ε — относительная диэлектрическая проницаемость. Понятие ёмкости также относится к системе проводников, в частности, к системе двух проводников, разделённых диэлектриком или вакуумом, — к конденсатору. В этом случае взаимная ёмкость этих проводников (обкладок конденсатора) будет равна отношению заряда, накопленного конденсатором, к разности потенциалов между обкладками. Для плоского конденсатора ёмкость равна:
где S — площадь одной обкладки (подразумевается, что они равны), d — расстояние между обкладками, ε — относительная диэлектрическая проницаемость среды между обкладками, ε0 = 8.854·10−12 Ф/м — электрическая постоянная.
25 билет:
Энергия электрического поля Опыт показывает, что заряженный конденсатор содержит запас энергии. Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор. Процесс
зарядки конденсатора можно представить
как последовательный перенос достаточно
малых порций заряда Δq > 0
с одной обкладки на другую (рис. 1.7.1).
При этом одна обкладка постепенно
заряжается положительным зарядом, а
другая – отрицательным. Поскольку
каждая порция переносится в условиях,
когда на обкладках уже имеется некоторый
заряд q,
а между ними существует некоторая
разность потенциалов Энергия Wе конденсатора емкости C, заряженного зарядом Q, может быть найдена путем интегрирования этого выражения в пределах от 0 до Q:
Формулу, выражающую энергию заряженного конденсатора, можно переписать в другой эквивалентной форме, если воспользоваться соотношением Q = CU.
Электрическую энергию Wе следует рассматривать как потенциальную энергию, запасенную в заряженном конденсаторе. Формулы для Wе аналогичны формулам для потенциальной энергии Eр деформированной пружины (см. ч. I, § 2.4)
где k – жесткость пружины, x – деформация, F = kx – внешняя сила. По современным представлениям, электрическая энергия конденсатора локализована в пространстве между обкладками конденсатора, то есть в электрическом поле. Поэтому ее называют энергией электрического поля. Это легко проиллюстрировать на примере заряженного плоского конденсатора. Напряженность однородного
поля в плоском конденсаторе равна E = U/d,
а его емкость
где V = Sd – объем пространства между обкладками, занятый электрическим полем. Из этого соотношения следует, что физическая величина
является электрической (потенциальной) энергией единицы объема пространства, в котором создано электрическое поле. Ее называют объемной плотностью электрической энергии. Энергия поля, созданного любым распределением электрических зарядов в пространстве, может быть найдена путем интегрирования объемной плотности wе по всему объему, в котором создано электрическое поле.
26 билет: Электронная проводимость металлов В начале XX века была создана классическая электронная теория проводимости металлов (П. Друде, 1900 г., Х.Лоренц, 1904 г.), которая дала простое и наглядное объяснение большинства электрических и тепловых свойств металлов. Рассмотрим некоторые положения этой теории. Свободные электроны Металлический проводник состоит из: 1) положительно заряженных ионов, колеблющихся около положения равновесия, и 2) свободных электронов, способных перемещаться по всему объему проводника. Таким образом, электрические свойства металлов обусловлены наличием в них свободных электронов с концентрацией порядка 1028 м–3, что примерно соответствует концентрации атомов. Эти электроны называются электронами проводимости. Они образуются путем отрыва от атомов металлов их валентных электронов. Такие электроны не принадлежат какому-то определенному атому и способны перемещаться по всему объему тела. В металле в отсутствие электрического поля электроны проводимости хаотически движутся и сталкиваются, чаще всего с ионами кристаллической решетки (рис. 1). Совокупность этих электронов можно приближенно рассматривать как некий электронный газ, подчиняющийся законам идеального газа. Средняя скорость теплового движения электронов при комнатной температуре составляет примерно 105 м/с. Условия существования электрического тока Для возникновения и поддержания тока в какой-либо среде необходимо выполнение двух условий: -наличие в среде свободных электрических зарядов -создание в среде электрического поля. В разных средах носителями электрического тока являются разные заряженные частицы. Электрическое поле в среде необходимо для создания направленного движения свободных зарядов. Как известно, на заряд q в электрическом поле напряженностью E действует сила F = q* E, которая и заставляет свободные заряды двигаться в направлении электрического поля. Признаком существования в проводнике электрического поля является наличие не равной нулю разности потенциалов между любыми двумя точками проводника, Однако, электрические силы не могут длительное время поддерживать электрический ток. Направленное движение электрических зарядов через некоторое время приводит к выравниванию потенциалов на концах проводника и, следовательно, к исчезновению в нем электрического поля. Для поддержания тока в электрической цепи на заряды кроме кулоновских сил должны действовать силы неэлектрической природы (сторонние силы). Устройство, создающее сторонние силы, поддерживающее разность потенциалов в цепи и преобразующее различные виды энергии в электрическую энергию, называется источником тока. Для существования электрического тока в замкнутой цепи необходимо включение в нее источника тока.
27 билет. Сила тока
Силой
тока называется физическая
величина
Сила тока в Международной системе единиц (СИ) измеряется в амперах.
По закону
Ома сила
тока
для
участка цепи прямо пропорциональна
приложенному напряжению
к
участку цепи и обратно
пропорциональна сопротивлению
Единица измерения в СИ — 1 Ампер (А) = 1 Кулон / секунду. Для измерения силы тока используют специальный прибор — амперметр (для приборов, предназначенных для измерения малых токов, также используются названия миллиамперметр, микроамперметр, гальванометр). Его включают в разрыв цепи в том месте, где нужно измерить силу тока. Основные методы измерения силы тока: магнитоэлектрический, электромагнитный и косвенный (путём измерения вольтметром напряжения на известном сопротивлении). В случае переменного тока различают мгновенную силу тока, амплитудную (пиковую) силу тока и эффективную силу тока (равную силе постоянного тока, который выделяет такую же мощность). Пло́тность то́ка — векторная физическая величина, имеющая смысл силы тока, протекающего через единицу площади. Например, при равномерном распределении плотности тока и всюду ортогональности ее плоскости сечения, через которое вычисляется или измеряется ток, величина вектора плотности тока:
где I - сила тока через поперечное сечение проводника площадью S (также см.рисунок).
В общем случае:
где Как видим из этого определения, сила тока есть поток вектора плотности тока через некую заданную фиксированную поверхность. В
простейшем предположении, что все
носители тока (заряженные частицы)
двигаются с одинаковым вектором
скорости
или
где
-
плотность заряда этих носителей.
(Направление вектора В реальности даже носители одного типа движутся вообще говоря и как правило с различными скоростями. Тогда под следует понимать среднюю скорость. В сложных системах (с различными типами носителей заряда, например, в плазме или электролитах)
то
есть вектор плотности тока есть сумма
плотностей тока по всем типам подвижных
носителей; где Выражение для общего случая может быть записано также через сумму по всем индивидуальным частицам:
(сама формула почти совпадает с формулой, приведенной чуть выше, но теперь индекс суммирования i означает не номер типа частицы, а номер каждой индивидуальной частицы, не важно, имеют они одинаковые заряды или разные, при этом концентрации оказываются уже не нужны). 28 билет. Связь тока и средней дрейфовой скорости Дрейфовая
скорость — средняя скорость упорядоченного
движения V, вызванная воздействием на
электроны с помощью внешнего поля. В
отсутствие внешнего электрического
поля электроны в кристалле совершают
только тепловое движение. Поэтому нет
преимущественных направлений движения,
и поэтому среднее значение тепловой
скорости равно нулю.
плотность тока связана с плотностью
свободных зарядов ρ и с дрейфовой
скоростью их движения
29 билет:
Закон Ома для однородного участка цепи, все точки которого имеют одинаковую температуру, выражается формулой (в современных обозначениях):
В таком виде формула закона Ома справедлива только для проводников конечной длины, так как входящие в это выражение величины I и U измеряются приборами, включенными на этом участке. Сопротивление R участка цепи зависит от длины l этого участка, поперечного сечения S и удельного сопротивления проводника ρ. Зависимость сопротивления от материала проводника и его геометрических размеров выражается формулой:
которая справедлива только для проводников постоянного сечения. Для проводников переменного сечения соответствующая формула не будет столь простой. В проводнике переменного сечения сила тока в различных сечениях будет одинаковой, однако плотность тока будет разной не только в различных сечениях, но даже и в различных точках одного и того же сечения. Различное значение будет иметь и напряженность, а, следовательно, и разность потенциалов на концах различных элементарных участков. Усредненные значения I, U и R по всему объему проводника не дают информации об электрических свойствах проводника в каждой его точке. Для успешного изучения электрических цепей необходимо получить выражение закона Ома в дифференциальной форме с тем, чтобы оно выполнялось в любой точке проводника любой формы и любых размеров. Зная
связь напряженности электрического
поля с разностью потенциалов на концах
некоторого участка
Обозначив
где
Оно выполняется в любой точке проводника, по которому течет электрический ток. Для замкнутой цепи следует учесть тот факт, что в ней, кроме напряженности поля кулоновских сил, действуют сторонние силы, создающие поле сторонних сил, характеризующееся напряженностьюЕст. С учетом этого закон Ома для замкнутой цепи в дифференциальной форме будет иметь вид:
В таком виде закон Ома входит в систему уравнений Максвелла, представляющую собой фундамент классической электродинамики.
30 билет. Закон Ома для участка цепи, сожержащего ЭДС.
Возьмем два участка цепи a-b и c-d (см. рис. 1) и составим для них уравнения в комплексной форме с учетом указанных на рис. 1 положительных направлений напряжений и токов. Объединяя оба случая, получим
или для постоянного тока
Формулы (1) и (2) являются аналитическим выражением закона Ома для участка цепи с источником ЭДС, согласно которому ток на участке цепи с источником ЭДС равен алгебраической сумме напряжения на зажимах участка цепи и ЭДС, деленной на сопротивление участка. В случае переменного тока все указанные величины суть комплексы. При этом ЭДС и напряжение берут со знаком “+”, если их направление совпадает с выбранным направлением тока, и со знаком “-”, если их направление противоположно направлению тока. 31 билет. закон Джоуля-Ленца в дифференциальной форме
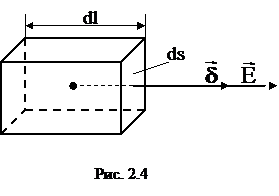
Мощность тепловых потерь в проводнике равна произведению тока и напряжения:
Если рассмотреть в проводящей среде элемент объема dV (рис. 2.4), то мощность, которая тратится в этом объеме на тепловые потери, будет равна:
откуда
(2.9) Следовательно, в единице объема проводящей среды в единицу времени выделяется энергия, численно равная gЕ2.
32 билет. Работа выхода. Термоэлектронная энергия. Работа выхода — разница между минимальной энергией (обычно измеряемой в электрон-вольтах), которую необходимо сообщить электрону для его «непосредственного» удаления из объёма твёрдого тела, и энергией Ферми. Здесь «непосредственность» означает то, что электрон удаляется из твёрдого тела через данную поверхность и перемещается в точку, которая расположена достаточно далеко от поверхности по атомным масштабам (чтобы электрон прошёл весь двойной слой), но достаточно близко по сравнению с размерами макроскопических граней кристалла. При этом пренебрегают дополнительной работой, которую необходимо затратить на преодоление внешних полей, возникающих из-за перераспределения поверхностных зарядов. Таким образом, работа выхода для одного и того же вещества для различных кристаллографических ориентаций поверхности оказывается различной. При удалении электрона на бесконечность его взаимодействие с зарядами, остающимися внутри твёрдого тела приводит к индуцированию макроскопических поверхностных зарядов (при рассмотрении полубесконечного образца в электростатике это называют «изображением заряда»). При перемещении электрона в поле индуцированного заряда совершается дополнительная работа, которая определяется диэлектрической проницаемостью вещества, геометрией образца и свойствами других поверхностей. За счет этого полная работа по перемещению электрона из любой точки образца в любую другую точку (в том числе и точку бесконечности) не зависит от пути перемещения, то есть от того, через какую поверхность был удален электрон. Поэтому в физике твёрдого тела эта работа не учитывается и не входит в работу выхода. Термоэлектро́нная эми́ссия (эффект Ричардсона, эффект Эдисона) — явление испускания электронов нагретыми телами. Концентрация свободных электронов в металлах достаточно высока, поэтому даже при средних температурах вследствие распределения электронов по скоростям (по энергии) некоторые электроны обладают энергией, достаточной для преодоления потенциального барьера на границе металла. С повышением температуры число электронов, кинетическая энергия теплового движения которых больше работы выхода, растет, и явление термоэлектронной эмиссии становится заметным. Исследование закономерностей термоэлектронной эмиссии можно провести с помощью простейшей двухэлектродной лампы — вакуумного диода, представляющего собой откачанный баллон, содержащий два электрода: катод К и анод А. В простейшем случае катодом служит нить из тугоплавкого металла (например, вольфрама), накаливаемая электрическим током. Анод чаще всего имеет форму металлического цилиндра, окружающего катод. Если диод включить в цепь, то при накаливании катода и подаче на анод положительного напряжения (относительно катода) в анодной цепи диода возникает ток. Если поменять полярность батареи, то ток прекращается, как бы сильно катод ни накаливали. Следовательно, катод испускает отрицательные частицы — электроны. Если
поддерживать температуру накаленного
катода постоянной и снять зависимость
анодного тока от анодного напряжения
— вольт-амперную характеристику, то
оказывается, что она не является
линейной, то есть для вакуумного
диода закон
Ома не
выполняется. Зависимость термоэлектронного
тока от анодного напряжения в области
малых положительных значений описывается
законом трех вторых (установлен русским
физиком С. А. Богуславским (1883— 1923) и
американским физиком И. Ленгмюром
(1881 — 1957)): При
увеличении анодного напряжения ток
возрастает до некоторого максимального
значения, называемого током насыщения.
Это означает, что почти все электроны,
покидающие катод, достигают анода,
поэтому дальнейшее увеличение
напряженности поля не может привести
к увеличению термоэлектронного тока.
Следовательно, плотность тока насыщения
характеризует эмиссионную способность
материала катода. Плотность тока
насыщения определяется формулой
Ричардсона — Дешмана, выведенной
теоретически на основе квантовой
статистики: На явлении термоэлектронной эмиссии основана работа многих вакуумных электронных приборов.
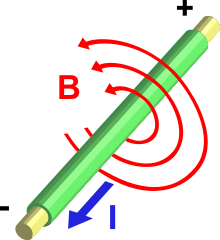
33 билет. Магнитное поле. Вектор магнитной индукции. Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения[1], магнитная составляющая электромагнитного поля[2] Магнитное поле может создаваться током заряженных частиц и/или магнитными моментамиэлектронов в атомах (и магнитными моментами других частиц, хотя в заметно меньшей степени) (постоянные магниты). Кроме этого, оно появляется при наличии изменяющегося во времени электрического поля. Основной
силовой характеристикой магнитного
поля является вектор
магнитной индукции Ещё одной фундаментальной характеристикой магнитного поля (альтернативной магнитной индукции и тесно с ней взаимосвязанной, практически равной ей по физическому значению) является векторный потенциал. Нередко
в литературе в качестве основной
характеристики магнитного поля в
вакууме (то есть в отсутствие магнитной
среды) выбирают не вектор магнитной
индукции Магнитное поле можно назвать особым видом материи[7], посредством которого осуществляется взаимодействие между движущимися заряженными частицами или телами, обладающими магнитным моментом. Магнитные поля являются необходимым (в контексте специальной теории относительности) следствием существования электрических полей. Вместе, магнитное и электрическое поля образуют электромагнитное поле, проявлениями которого являются, в частности, свет и все другие электромагнитные волны.
Электрический ток(I), проходя по проводнику, создаёт магнитное поле (B) вокруг проводника. С точки зрения квантовой теории поля магнитное взаимодействие — как частный случай электромагнитного взаимодействия переносится фундаментальным безмассовым бозоном — фотоном (частицей, которую можно представить как квантовое возбуждение электромагнитного поля), часто (например, во всех случаях статических полей) — виртуальным. Вектор магнитной индукции - это основная силовая характеристика магнитного поля (обозначается В). Пробный контур, помещенный в магнитное поле, испытывает со стороны магнитного поля действие вращающего момента сил М. Опытным путем было установлено, что для одной и той же точки магнитного поля максимальный вращающий момент М (момент сил) пропорционален произведению силы тока I в контуре на его площадь S. Величину IS называют магнитным моментом контура Pm.
34 билет: Закон Ампера в векторной форме: dF = I [dl B] Сила Ампера направлена перпендикулярно плоскости, в которой лежат векторы dl и B. Для определения направления силы, действующей на проводник с током, помещенный в магнитное поле, применяется правило левой руки.
Правило левой руки Если левую руку расположить так, чтобы линии магнитной индукции входили в ладонь, а вытянутые четыре пальца совпадали с направлением тока в проводнике, то отогнутый большой палец укажет направление силы, действующей на проводник с током, помещенный в магнитное поле. 35 билет. Сила Лоренца в векторной форме. Сила
Лоренца - сила, действующая со стороны
магнитного поля на движущийся заряд.
Эмпирически получаем Принято
правило левой руки (для «+» заряда для
нахождения направления силы Лоренца):
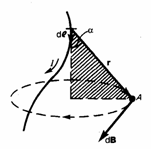
если вектор
36 билет: Закон Био Савара Лапласа определяет величину модуля вектора магнитной индукции в точке выбранной произвольно находящейся в магнитном поле. Поле при этом создано постоянным током на некотором участке. Формулировка закона Био Савара Лапласа имеет вид: При прохождении постоянного тока по замкнутому контуру, находящемуся в вакууме, для точки, отстоящей на расстоянии r0, от контура магнитная индукция будет иметь вид.
Формула 1 — Закон Био Савара Лапласа где I ток в контуре гамма контур, по которому идет интегрирование r0 произвольная точка Возьмём элементарный участок проводника с током dl, он будет создавать в некоторой точке индукцию магнитного поля dB. dl это элементарный вектор направление, которого совпадает с направлением тока в контуре. r радиус вектор, направленный от dl к точке наблюдения. А вектор dB направлен перпендикулярно элементарному участку проводника dl и одновременно перпендикулярно радиус вектору r. То есть, проще говоря, элементарный вектор индукции dB направлен перпендикулярно плоскости образованной вектором dl и r. А его направление совпадает с направлением касательной к магнитной индукции. Определить это направление можно с помощью правела правого винта. Применяется оно таким образом.
Рисунок 1 — иллюстрация к закону Био Савара Лапласа
В случае если поступательное движение винта направлено в сторону движения тока, то направление вращения головки винта указывает направление dB.
37 билет: Закон полного тока Циркуляцией
вектора
где
–
замкнутый контур произвольной
формы; Закон полного тока для магнитного поля в вакууме: циркуляция вектора индукции магнитного поля вдоль замкнутого контура в вакууме пропорциональна алгебраической сумме токов, охватываемых этим контуром:
где
Закон справедлив для проводников с токами любой формы и любых размеров. 38 билет: Магни́тный моме́нт, магни́тный дипо́льный моме́нт — основная величина, характеризующаямагнитные свойства вещества. Источником магнетизма, согласно классической теории электромагнитных явлений, являются электрические макро- и микротоки. Элементарным источником магнетизма считают замкнутый ток. Магнитным моментом обладают элементарные частицы, атомные ядра, электронные оболочки атомов и молекул. Магнитный момент элементарных частиц (электронов,протонов, нейтронов и других), как показала квантовая механика, обусловлен существованием у них собственного механического момента — спина. Магнитный момент измеряется в А⋅м2 или Дж/Тл (СИ), либо эрг/Гс (СГС), 1 эрг/Гс = 10-3 Дж/Тл. Специфической единицей элементарного магнитного момента является магнетон Бора. В случае плоского контура с электрическим током магнитный момент вычисляется как
где
— сила
тока в
контуре,
—
площадь контура, Для произвольного замкнутого контура магнитный момент находится из:
где В общем случае произвольного распределения токов в среде:
где Рассмотрим поведение в магнитном поле прямоугольной рамки с током, имеющей неподвижную ось. Силы Ампера, действуют на стороны рамки, ориентированные перпендикулярно к силовым линиям. Эти силы создадут пару сил, момент которых будет поворачивать рамку вокруг оси: сначала момент будет увеличивать угловую скорость рамки, пока она не встанет перпендикулярно к силовым линиям поля, затем по инерции рамка будет продолжать движение, но момент пары сил будет ее тормозить до тех пор, пока не остановит в положении, симметричном начальному. Затем рамка начнет двигаться в обратном направлении. Возникнут крутильные колебания рамки. Если в тот момент, когда рамка встанет перпендикулярно к силовым линиям поля, изменить направление тока на прямо противоположное, то рамка будет вращаться в одном направлении. По такому принципу работает двигатель постоянного тока.
39 билет: Поток вектора магнитной индукции, пронизывающий площадку S - это величина, равная:
Поток вектора магнитной индукции (магнитный поток) измеряется в веберах (Вб)
Магнитный поток - величина скалярная. Поток вектора магнитной индукции (магнитный поток) равен числу линий магнитной индукции, проходящих сквозь данную поверхность. Поток вектора магнитной индукции (магнитный поток) сквозь произвольную замкнутую поверхность равен нулю:
40 билет. Теорема О-Г для магнитного поля. Поток вектора магнитной индукции (магнитный поток) сквозь произвольную замкнутую поверхность равен нулю:
Это теорема Остроградского-Гаусса для магнитного поля. Она свидетельствует о том, что в природе не существует магнитных зарядов – физических объектов, на которых бы начинались или заканчивались линии магнитной индукции. Поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:
или в дифференциальной форме
Это эквивалентно тому, что в природе не существует «магнитных зарядов» (монополей), которые создавали бы магнитное поле, как электрические заряды создают электрическое поле[5]. Иными словами, теорема Гаусса для магнитной индукции показывает, что магнитное поле является (полностью) вихревым.
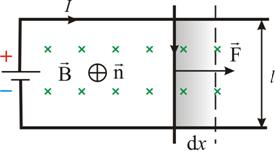
41 билет. Работа по перемещению проводника с током в магнитном поле. Рассмотрим
контур с током, образованный неподвижными
проводами и скользящей по ним подвижной
перемычкой длиной l (рис. 2.17). Этот
контур находится во внешнем однородном
магнитном поле
Рис. 2.17 На элемент тока I (подвижный провод) длиной l действует сила Ампера, направленная вправо:
Пусть проводник l переместится параллельно самому себе на расстояние dx. При этом совершится работа:
Итак,
Работа, совершаемая проводником с током при перемещении, численно равна произведению тока на магнитный поток, пересечённый этим проводником. Формула остаётся справедливой, если проводник любой формы движется под любым углом к линиям вектора магнитной индукции.
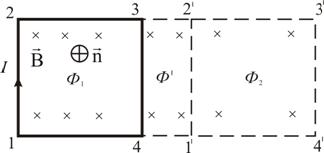
42 билет. работа по перемещению замкнутого контура с током в магнитном поле Выведем выражение для работы по перемещению замкнутого контура с током в магнитном поле. Рассмотрим
прямоугольный контур с током 1-2-3-4-1
(рис. 2.18). Магнитное поле направлено
от нас перпендикулярно плоскости
контура. Магнитный поток
Рис. 2.18 Переместим
этот контур параллельно самому себе
в новое положение 1'-2'-3'-4'-1'. Магнитное
поле в общем случае может быть
неоднородным и новый контур будет
пронизан магнитным потоком Площадка
4-3-2'-1'-4, расположенная между старым и
новым контуром, пронизывается
потоком Полная работа по перемещению контура в магнитном поле равна алгебраической сумме работ, совершаемых при перемещении каждой из четырех сторон контура:
где
Провод
1–2 перерезает поток (
Тогда общая работа по перемещению контура
здесь Работа, совершаемая при перемещении замкнутого контура с током в магнитном поле, равна произведению величины тока на изменение магнитного потока, сцепленного с этим контуром. Элементарную работу по бесконечно малому перемещению контура в магнитном поле можно найти по формуле
Выражения (2.9.1) и (2.9.5) внешне тождественны, но физический смысл величины dФ различен. Соотношение
(2.9.5), выведенное нами для простейшего
случая, остаётся справедливым для
контура любой формы в произвольном
магнитном поле. Более того, если контур
неподвижен, а меняется
43 билет. Законы фарадея. Правило Ленца. Первый закон электролиза Фарадея: масса вещества, осаждённого на электроде при электролизе, прямо пропорциональна количеству электричества, переданного на этот электрод. Под количеством электричества имеется в видуэлектрический заряд, измеряемый, как правило, в кулонах. Второй закон электролиза Фарадея: для данного количества электричества (электрического заряда) масса химического элемента, осаждённого на электроде, прямо пропорциональна эквивалентной массе элемента. Эквивалентной массой вещества является его молярная масса, делённая на целое число, зависящее от химической реакции, в которой участвует вещество. [править]Математический вид Законы Фарадея можно записать в виде следующей формулы:
где: m — масса осаждённого на электроде вещества в граммах Q — полный электрический заряд, прошедший через вещество F = 96 485,3383(83) Кл·моль−1 — постоянная Фарадея M — молярная масса вещества z — валентное число ионов вещества (число электронов на один ион). Заметим, что M/z — это эквивалентная масса осаждённого вещества. Для первого закона Фарадея M, F и z являются константами, так что чем больше величина Q, тем больше будет величина m. Для второго закона Фарадея Q, F и z являются константами, так что чем больше величина M/z (эквивалентная масса), тем больше будет величина m. В
простейшем случае
постоянного тока электролиза
и тогда
где: n — выделенное количество вещества («количество молей»): n = m/M t — время действия постоянного тока. В
более сложном случае переменного
электрического тока полный
заряд Q тока I(
Здесь t — полное время электролиза. Обратите внимание, что тау используется в качестве переменной, ток I является функцией от тау.[2]
Направление индукционного тока в контуре определяется правилом Ленца: Индукционный ток направлен так, чтобы своим магнитным полем противодействовать изменению магнитного потока, которым он вызван.
44 билет. Явление самоиндукции. Индуктивность. Замыкание
цепи
Размыкание
цепи
ИНДУКТИВНОСТЬ От
чего зависит ЭДС самоиндукции?
Эл.ток
создает собственное магнитное поле
. Магнитный поток через контур
пропорционален индукции магнитного
поля (Ф ~ B), индукция пропорциональна
силе тока в проводнике
(B ~ I),
следовательно магнитный поток
пропорционален силе тока (Ф ~ I).
ЭДС
самоиндукции зависит от скорости
изменения силы тока в эл.цепи, от
свойств проводника
(размеров и
формы) и от относительной магнитной
проницаемости среды, в которой находится
проводник.
Физическая величина,
показывающая зависимость ЭДС
самоиндукции от размеров и формы
проводника и от среды, в которой
находится проводник, называется
коэффициентом самоиндукции или
индуктивностью.
Единицы измерения индуктивности в системе СИ:
Индуктивность катушки зависит от: числа витков, размеров и формы катушки и от относительной магнитной проницаемости среды ( возможен сердечник).
45 билет:
Взаимоиндукция (взаимная индукция) — возникновение электродвижущей силы (ЭДС индукции) в одном проводнике вследствие изменения силы тока в другом проводнике или вследствие изменения взаимного расположения проводников. Взаимоиндукция — частный случай более общего явления — электромагнитной индукции. При изменении тока в одном из проводников или при изменении взаимного расположения проводников происходит изменение магнитного потока через (воображаемую) поверхность, "натянутую" на контур второго, созданного магнитным полем, порожденным током в первом проводнике, что по закону электромагнитной индукции вызывает возникновение ЭДС во втором проводнике. Если второй проводник замкнут, то под действием ЭДС взаимоиндукции в нём образуется индуцированный ток. И наоборот, изменение тока во второй цепи вызовет появление ЭДС в первой. Направление тока, возникшего при взаимоиндукции, определяется по правилу Ленца. Правило указывает на то, что изменение тока в одной цепи (катушке) встречает противодействие со стороны другой цепи (катушки). Чем большая часть магнитного поля первой цепи пронизывает вторую цепь, тем сильнее взаимоиндукция между цепями. С количественной стороны явление взаимоиндукции характеризуется взаимной индуктивностью (коэффициентом взаимоиндукции, коэффициентом связи). Для изменения величины индуктивной связи между цепями, катушки делают подвижными. Приборы, служащие для изменения взаимоиндукции между цепями, называются вариометрами связи. Явление взаимоиндукции широко используется для передачи энергии из одной электрической цепи в другую, для преобразования напряжения с помощью трансформатора. Режимом холостого хода трансформатора называют режим работы при питании одной из обмоток трансформатора от источника с переменным напряжением и при разомкнутых цепях других обмоток. Такой режим работы может быть у реального трансформатоpa, когда он подключен к сети, а нагрузка, питаемая от его вторичной обмотки, еще не включена. По первичной обмотке трансформатора проходит ток I0, в то же время во вторичной обмотке тока нет, так как цепь ее разомкнута. Ток I0, проходя по первичной обмотке, создает в магнитопроводе синусоидально изменяющийся лоток Ф0, который из-за магнитных потерь отстает по фазе от тока на угол потерь δ. Очевидно, что переменный магнитный поток Ф0 пересекает обе обмотки трансформатора. В каждой из них возникают эдс: в первичной обмотке — эдс самоиндукции Е1, во вторичной обмотке — эдс взаимоиндукции Е2. Действующие значения этих эдс зависят от числа витков в обмотках, магнитного потока Ф0 и частоты его изменения f. Величины эдс определяют по формулам: Е1 = 4,44fω1Ф0 макс10-8В, Е2 = 4,44fω2Ф2 макс10-8В, где ω1 и ω2 — числа витков в обмотках; f — частота, Гц; Ф0 макс — максимальное значение магнитного потока, Вб. Разделив Е1 на Е2, получим Е1 / Е2 = ω1 / ω2. Это соотношение характеризует одно из основных свойств трансформатора: эдс в обмотках трансформатора пропорциональны количеству витков. Отношение числа витков ω1 / ω2 = k называют коэффициентом трансформации. Таким образом, если мы хотим повысить полученное от генератора напряжение в 10, 100 или 1000 раз, то необходимо так подобрать обмотки трансформатора, чтобы число витков ω2 вторичной обмотки было больше числа витков ω1 первичной обмотки соответственно в 10, 100 или 1000 раз. Тогда вторичная обмотка оказывается обмоткой высшего напряжения (ВН), а первичная — обмоткой низшего напряжения (НН). Наоборот, если необходимо снизить напряжение в линии, первичное напряжение подводят к обмотке ВН, а к обмотке НН подключают приемники электрической энергии. Итак, любой трансформатор может работать как повышающий и как понижающий. Все зависит от того, к какой из его обмоток будет подведено напряжение для преобразования. Обмотка трансформатора, к которой подводится энергия преобразуемого переменного тока, называется первичной (независимо от того, будет ли эта обмотка высшего или низшего напряжения). Обмотка трансформатора, от которой отводится энергия преобразованного переменного тока, называется вторичной. Мы рассмотрели действие только рабочего, или основного, магнитного потока Ф0. Однако в трансформаторе кроме рабочего существует еще магнитный поток рассеяния Фр1. Этот магнитный поток образуется силовыми линиями, которые ответвляются от основного потока в сердечнике и замыкаются по воздуху вокруг витков обмотки ω1. Поскольку поток рассеяния замыкается по воздуху, его величина пропорциональна току, в нашем случае — току холостого хода I0. Следовательно, поток рассеяния Фр1 является, как и ток I0, переменным и, пересекая витки первичной обмотки, создает в ней эдс самоиндукции Ер1. В первичной обмотке трансформатора создаются две эдс самоиндукции: одна E1 — рабочим магнитным потоком Ф0, другая Ер1 — магнитным потоком рассеяния. Мы знаем, что эдс самоиндукции всегда направлена против приложенного напряжения и ее действие на ток в цепи равносильно добавочному сопротивлению, которое называют индуктивным и обозначают х. Для поддержания неизменным тока холостого хода подводимое напряжение U1 должно расходоваться не только на преодоление активного сопротивления r1 обмотки, но и на создание эдс самоиндукции. Другими словами, приложенное напряжение U1 складывается из нескольких частей: первая часть равна эдс самоиндукции E1 от потока Ф0, вторая — эдс самоиндукции Ер1от потока рассеяния Фр1, третья — активному падению напряжения I0r1.
46 билет. атом в магнитном поле. При
внесении атома в магнитное поле с
индукцией
на
электрон, движущийся по орбите,
эквивалентной замкнутому контуру с
током, действует момент сил
При этом изменяется орбитальный момент импульса электрона:
Аналогично изменяется вектор орбитального магнитного момента электрона:
Из
этого следует, что векторы
Рис. 6.2 Эта
прецессия называется ларморовской
прецессией.
Угловая скорость этой прецессии
Теорема Лармора: единственным результатом влияния магнитного поля на орбиту электрона в атоме является прецессия орбиты и вектора – орбитального магнитного момента электрона с угловой скоростью вокруг оси, проходящей через ядро атома параллельно вектору индукции магнитного поля. Прецессия орбиты электрона в атоме приводит к появлению дополнительного орбитального тока, направленного противоположно току I:
и
соответствующего ему наведенного
орбитального магнитного момента
где
47 билет: Вектор намагниченности ("намагничения") Если вещество помещено во внешнее магнитное поле, то в атомах или молекулах этого вещества появляются токи связанных зарядов (плотность которых обозначим через Jin). Таким образом в атомах возникают магнитные моменты от Jin. В результате, в веществе возникает суммарный магнитный момент илинамагниченность. Для описания свойств намагниченности можно ввести понятие магнитного момента единицы объема M по следующему определению:
где = M — вектор намагниченности m - вектор магнитного момента; V — объём , занимаемый веществом Вектор намагниченности - это магнитный момент единицы объёма вещества. Классификация магнетиков. В то время как диэлектрическая проницаемость ε у всех веществ всегда больше единицы (диэлектрическая восприимчивость κ>0), магнитная проницаемость μ может быть как больше единицы, так и меньше единицы (соответственно магнитная восприимчивость χ >0 и χ<0). Поэтому магнитные свойства веществ отличаются гораздо большим разнообразием, чем электрические свойства. По классификации В.Л.Гинзбурга (Нобелевская премия по физике, 2004г.) можно выделить шесть типов магнетиков. Они перечислены в приводимой ниже таблице. Таблица. Современная классификация магнетиков.
Дадим краткую характеристику каждого типа магнетика. Диамагнетики
– вещества, характеризуемые отрицательным
значением магнитной восприимчивости
χ. Вследствие этого вектор намагничивания Парамагнетики – характеризуются положительным значение χ , ведут они себя подобно диэлектрикам с диэлектрической проницаемостью ε>1, то есть вектор в этих веществах параллелен намагничивающему полю . К парамагнетикам относятся алюминий (χ = 2,1∙10-6), платина (χ = 3∙10-4), хлористое железо (χ = 2,5∙10-3). Ферромагнетики
– особый вид магнетиков, отличающийся
от других магнетиков следующими
характерными признаками: 1) высоким
значением магнитной восприимчивости
(см. таблицу); 2) зависимостью магнитной
проницаемости μ от напряженности
магнитного поля, вследствие чего
зависимость Ферримагнетики (ферриты) – вещества, в которых магнитные моменты атомов кристаллической решетки образуют несколько магнитных подрешеток с магнитными моментами, направленными навстречу друг другу. Имея меньшую величину магнитной восприимчивости по сравнению с ферромагнетиками, в остальном ферримагнетики характеризуются теми же признаками, что и ферромагнетики. Типичными ферритами являются соединения оксидов железа с оксидами других металлов - шпинели (MnFe2O4), гранаты Gd3Fe5O12), гексаферриты (PbFe12O19). Другую группу ферритов образуют двойные фториды типа RbNiF3, а также соединения типа RFe2 (R – редкоземельный металл). Антиферромагнетики – частный случай ферримагнетиков, в которых магнитные моменты подрешеток с противоположно направленными магнитными моментами полностью компенсируют друг друга (скомпенсированный ферримагнетик). Существование антиферромагнетиков было предсказано Л.Д.Ландау в 1933г. В настоящее время известен широкий спектр веществ, обладающих антиферромагнитными свойствами: редкоземельные элементы (Er, Dy, Ho), оксиды и дифториды некоторых металлов (FeO, MnO, CoF2, NiF2), соли угольной и серной кислот (MnCO3, NiSO4) и другие. Сверхдиамагнетики (идеальные диамагнетики) – вещества, магнитная прони-цаемость μ которых равна нулю. Благодаря этой особенности для сверхдиамагнетиков имеет место эффект Мейсснера-Оксенфельда (Meissner W., 1882-1974; Ocksenfeld C.) – полное выталкивание магнитного поля из объема сверхдиамагнетика (магнитная индукция =0). Сверхдиамагнетиками являются все вещества, находящиеся в сверхпроводящем состоянии - низкотемпературные сверхпроводники (металлы) и высокотемпературные сверхпроводники (керамики). Из несверхпроводящих материалов, обладающих сверхдиамагнитными свойствами, известен пока только один пример – хлорид меди (CuCl), открытый в 1986г. (Русаков А.П., МИ
48 билет Напряженностью
магнитного поля называют
векторную величину
Напряженность магнитного поля заряда q, движущегося в вакууме равна:
Это выражение показывает закон Био–Савара–Лапласа для . Напряженность
магнитного поля
является,
как бы, аналогом вектора электрического
смещения
Относительная магнитная проницаемость показывает, во сколько раз в данной среде сила взаимодействия между проводами с током изменяется по сравнению с вакуумом. Численно равна отношению абсолютной магнитной проницаемости к магнитной постоянной. Абсолютная магнитная проницаемость равна произведению магнитной проницаемости на магнитную постоянную. 49 билет. Закон полного тока. Магнитное поле в веществе является суперпозицией двух полей – внешнего, создаваемого макротоками, и внутреннего, создаваемого микротоками.
Вклад дают только те токи, которые нанизаны на замкнутый контур L. Элементу dl этого контура соответствует ток
Полная величина тока определится
Циркуляцию вектора магнитной индукции в веществе можно представить
С учетом определения микротоков можно записать
Таким образом, закон полного тока для магнитного поля в веществе будет иметь вид
Учитывая, что намагниченность зависит от магнитной индукции внешнего магнитного поля
С напряженностью магнитного поля намагниченность изотропной среды связана соотношением
Согласно теореме Остроградского-Гаусса
Согласно теореме о циркуляции вектора Н
При переходе через границу нормальная составляющая В и тангенциальная составляющая Н изменяются непрерывно, а нормальная составляющая Н и тангенциальная составляющая В испытывают скачок. При пересечении границы под углом линии преломляются
Магнитной цепью называется последовательность тел, через которые проходят линии магнитной индукции. Закон Ома для неразветвленной замкнутой магнитной цепи
Магнитное сопротивление однородного участка магнитной цепи
Узлом магнитной цепи называется место ее разветвления Алгебраическая сумма магнитных потоков во всех n участках, сходящихся в узле, равна нулю (первое правило Кирхгофа – вытекает из теоремы Остроградского-Гаусса)
В любой замкнутой магнитной цепи, произвольно выбранной в разветвленной магнитной цепи, алгебраическая сумма произведений магнитных потоков на магнитные сопротивления соответствующих участков цепи равна алгебраической сумме магнитодвижущих сил в этой цепи
Энергия
магнитного поля в магнетике, для
которого соблюдается линейная
зависимость между J и В (диамагнетики
и парамагнетики), может быть
выражена
При малом изменении состояния системы закон сохранения энергии можно выразить в виде
Если
система квазистатическая (можно
пренебречь изменением кинетической
энергии), а работа внешних сил
(пондемоторных) равна работе сил,
действующих на тела системы
Для неподвижного контура с током
Если
ток в контуре нарастает от 0 до
Конец формы
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

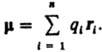 В молекулах и
мол. системах центры положит. зарядов
qА совпадают
с положениями атомных
ядер (радиусы-векторы rA),
а электронное распределение описывается
плотностью вероятности (r). В
этом случае дипольный
момент
В молекулах и
мол. системах центры положит. зарядов
qА совпадают
с положениями атомных
ядер (радиусы-векторы rA),
а электронное распределение описывается
плотностью вероятности (r). В
этом случае дипольный
момент 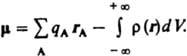 Вектор дипольного
момента направлен от центра тяжести
отрицат. зарядов к центру тяжести
положительных. В хим. литературе
дипольному моменту молекулы иногда
приписывают противоположное направление.
Часто вводят представление о дипольных
моментах отдельных хим. связей,
векторная сумма к-рых дает дипольный
момент молекулы.
При этом дипольный момент связи
определяют двумя положит. зарядами
ядер атомов,
образующих связь, и распределением
отрицат. (электронного) заряда. Дипольный
момент хим. связи обусловлен смещением
электронного облака в сторону одного
из атомов.
Связь наз. полярной, если соответствующий
дипольный момент существенно отличается
от нуля. Возможны случаи, когда отдельные
связи в молекуле
полярны, а суммарный дипольный
момент молекулы равен
нулю; такиемолекулы наз.
неполярными (напр., молекулы СО2 и CCl4).
Если же дипольный момент молекулы отличен
от нуля, молекула наз.
полярной. Напр., молекула Н2О
полярна; суммирование дипольных
моментов двух полярных связей ОН также
дает отличный от нуля дипольный момент,
направленный по биссектрисевалентного
угла НОН. Порядок величины
дипольного момента молекулы определяется
произведением зарядаэлектрона (1,6.1019 Кл)
на длину хим. связи (порядка 1010 м),
т. е. составляет 1029 Кл.м.
В справочной литературе дипольные
моменты молекул приводят
в дебаях (Д или D), по имени П. Дебая; 1 Д
= 3,33564.1030Кл.м. Спектроскопич.
методы определения дипольных
моментов молекул основаны
на эффектах расщепления и сдвига
спектральных линий в электрич. поле
(эффект
Штарка). Для линейных молекул и молекул типа
симметричного волчка известны точные
выражения, связывающие дипольный
момент со штарковским расщеплением
линий вращательных
спектров. Этот метод дает наиб.
точные значения величины дипольного
момента (до 104 Д),
причем экспериментально определяется
не только величина, но и
направление векторадипольного
момента. Важно, что точность определения
дипольного момента почти не зависит
от его абс. величины. Это позволило
получить весьма точные значения очень
малых дипольных моментов
ряда молекулуглеводородов,
к-рые нельзя надежно определить др.
методами. Так, дипольный момент пропана равен
0,085b 0,001 Д, пропилена 0,364 b 0,002
Д, пропина 0,780 b 0,001
Д, толуола 0,375 b 0,01
Д, азулена 0,796 b 0,01
Д. Область применения метода микроволновой
спектроскопии ограничена, однако,
небольшими молекулами,
не содержащими атомов тяжелых
элементов. Направление вектора дипольного
момента молекулы м.
б. определено экспериментально и
по Зеемана
эффекту второго порядка. Др.
группа методов определения дипольного
момента основана на измерениях
диэлектрич. проницаемости е в-ва. Этими
методами измерены дипольные
моменты молекул более
10 тыс. в-в. Переход от измеряемого
значения газа,
чистой жидкости или
разбавл. р-ра, т. е. макроскопич.
характеристики диэлектрика,
к величине дипольного момента основан
на теории поляризации диэлектриков.
Считается, что при наложении электрич.
поля на диэлектрик его
полнаяполяризация Р (средний
дипольный момент единицы объема)
складывается из наведенной, или
индуцированной, поляризации Рм и
ориентационной поляризации Рор и
связана с ур-нием Ланжевена -
Дебая:
Вектор дипольного
момента направлен от центра тяжести
отрицат. зарядов к центру тяжести
положительных. В хим. литературе
дипольному моменту молекулы иногда
приписывают противоположное направление.
Часто вводят представление о дипольных
моментах отдельных хим. связей,
векторная сумма к-рых дает дипольный
момент молекулы.
При этом дипольный момент связи
определяют двумя положит. зарядами
ядер атомов,
образующих связь, и распределением
отрицат. (электронного) заряда. Дипольный
момент хим. связи обусловлен смещением
электронного облака в сторону одного
из атомов.
Связь наз. полярной, если соответствующий
дипольный момент существенно отличается
от нуля. Возможны случаи, когда отдельные
связи в молекуле
полярны, а суммарный дипольный
момент молекулы равен
нулю; такиемолекулы наз.
неполярными (напр., молекулы СО2 и CCl4).
Если же дипольный момент молекулы отличен
от нуля, молекула наз.
полярной. Напр., молекула Н2О
полярна; суммирование дипольных
моментов двух полярных связей ОН также
дает отличный от нуля дипольный момент,
направленный по биссектрисевалентного
угла НОН. Порядок величины
дипольного момента молекулы определяется
произведением зарядаэлектрона (1,6.1019 Кл)
на длину хим. связи (порядка 1010 м),
т. е. составляет 1029 Кл.м.
В справочной литературе дипольные
моменты молекул приводят
в дебаях (Д или D), по имени П. Дебая; 1 Д
= 3,33564.1030Кл.м. Спектроскопич.
методы определения дипольных
моментов молекул основаны
на эффектах расщепления и сдвига
спектральных линий в электрич. поле
(эффект
Штарка). Для линейных молекул и молекул типа
симметричного волчка известны точные
выражения, связывающие дипольный
момент со штарковским расщеплением
линий вращательных
спектров. Этот метод дает наиб.
точные значения величины дипольного
момента (до 104 Д),
причем экспериментально определяется
не только величина, но и
направление векторадипольного
момента. Важно, что точность определения
дипольного момента почти не зависит
от его абс. величины. Это позволило
получить весьма точные значения очень
малых дипольных моментов
ряда молекулуглеводородов,
к-рые нельзя надежно определить др.
методами. Так, дипольный момент пропана равен
0,085b 0,001 Д, пропилена 0,364 b 0,002
Д, пропина 0,780 b 0,001
Д, толуола 0,375 b 0,01
Д, азулена 0,796 b 0,01
Д. Область применения метода микроволновой
спектроскопии ограничена, однако,
небольшими молекулами,
не содержащими атомов тяжелых
элементов. Направление вектора дипольного
момента молекулы м.
б. определено экспериментально и
по Зеемана
эффекту второго порядка. Др.
группа методов определения дипольного
момента основана на измерениях
диэлектрич. проницаемости е в-ва. Этими
методами измерены дипольные
моменты молекул более
10 тыс. в-в. Переход от измеряемого
значения газа,
чистой жидкости или
разбавл. р-ра, т. е. макроскопич.
характеристики диэлектрика,
к величине дипольного момента основан
на теории поляризации диэлектриков.
Считается, что при наложении электрич.
поля на диэлектрик его
полнаяполяризация Р (средний
дипольный момент единицы объема)
складывается из наведенной, или
индуцированной, поляризации Рм и
ориентационной поляризации Рор и
связана с ур-нием Ланжевена -
Дебая:
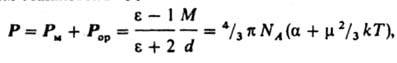 где
М - мол. масса, d -
плотность, - поляризуемость молекулы,
NA - число
Авогадро, k - постоянная
Больцмана, Т - абс. т-ра. Измерения
диэлектрич. проницаемости проводят
в постоянном поле или при низких
частотах, обеспечивающих полную
ориентацию молекул по
полю. При наиб. распространенном
варианте метода - измерениях в разбавл.
р-рах неполярных р-рителей - предполагается
аддитивность поляризаций
растворенного в-ва и р-рителя.
Важнейшая область применения
данных о дипольных моментах молекул -структурные
исследования, установление конформации
молекул, конформационного и изомерного
состава в-ва, его зависимости от т-ры.
Величины дипольных моментов молекул позволяют
судить о распределении
электронной плотности в молекулах и
зависимости этого распределения от
характера отдельных заместителей.
В общем случае структурная интерпретация
дипольных моментов требует сравнения
эксперим. величин со значениями,
полученными квантовомех. расчетом
либо при помощи аддитивной векторной
схемы с использованием дипольных
моментов отдельных связей и атомных
групп. Последние находят либо по
интенсивностям колебат. полос
поглощения, либо путем векторного
разложения дипольных моментов нек-рых
симметричныхмолекул.
Расчеты с использованием векторной
аддитивной схемы могут учитывать
разл. проявления стереохим. нежесткости,
напр., затрудненное или своб. внутр.
вращение молекулы.
Высокосимметричные мол. структуры,
обладающие центром инверсии,
двумя взаимно перпендикулярными осями
вращения или осями, перпендикулярными
плоскости симметрии,
не должны иметь дипольных моментов.
По наличию или отсутствию дипольного
момента молекулы можно
в отдельных случаях выбрать для нее
ту или иную структуру без к.-л. теоретич.
расчетов. Так, равенство нулю эксперим.
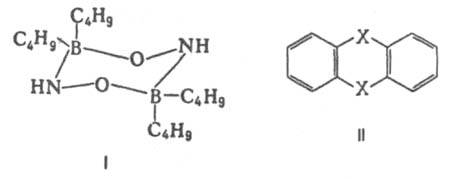
дипольного момента димера
аминооксидибутилборана (ф-ла I) служит
доказательством того, что он существует
в виде устойчивой кресловидной конформации,
обладающей центром инверсии.
Наоборот, наличие дипольного момента
у тиантрена (ф-ла II, X = S) и селенантрена
(II, X = Se), равных 1,57 Д и 1,41 Д соотв.,
исключает для них центросимметричную
структуру, в частности плоскую.
где
М - мол. масса, d -
плотность, - поляризуемость молекулы,
NA - число
Авогадро, k - постоянная
Больцмана, Т - абс. т-ра. Измерения
диэлектрич. проницаемости проводят
в постоянном поле или при низких
частотах, обеспечивающих полную
ориентацию молекул по
полю. При наиб. распространенном
варианте метода - измерениях в разбавл.
р-рах неполярных р-рителей - предполагается
аддитивность поляризаций
растворенного в-ва и р-рителя.
Важнейшая область применения
данных о дипольных моментах молекул -структурные
исследования, установление конформации
молекул, конформационного и изомерного
состава в-ва, его зависимости от т-ры.
Величины дипольных моментов молекул позволяют
судить о распределении
электронной плотности в молекулах и
зависимости этого распределения от
характера отдельных заместителей.
В общем случае структурная интерпретация
дипольных моментов требует сравнения
эксперим. величин со значениями,
полученными квантовомех. расчетом
либо при помощи аддитивной векторной
схемы с использованием дипольных
моментов отдельных связей и атомных
групп. Последние находят либо по
интенсивностям колебат. полос
поглощения, либо путем векторного
разложения дипольных моментов нек-рых
симметричныхмолекул.
Расчеты с использованием векторной
аддитивной схемы могут учитывать
разл. проявления стереохим. нежесткости,
напр., затрудненное или своб. внутр.
вращение молекулы.
Высокосимметричные мол. структуры,
обладающие центром инверсии,
двумя взаимно перпендикулярными осями
вращения или осями, перпендикулярными
плоскости симметрии,
не должны иметь дипольных моментов.
По наличию или отсутствию дипольного
момента молекулы можно
в отдельных случаях выбрать для нее
ту или иную структуру без к.-л. теоретич.
расчетов. Так, равенство нулю эксперим.
дипольного момента димера
аминооксидибутилборана (ф-ла I) служит
доказательством того, что он существует
в виде устойчивой кресловидной конформации,
обладающей центром инверсии.
Наоборот, наличие дипольного момента
у тиантрена (ф-ла II, X = S) и селенантрена
(II, X = Se), равных 1,57 Д и 1,41 Д соотв.,
исключает для них центросимметричную
структуру, в частности плоскую.
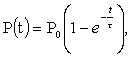
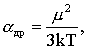

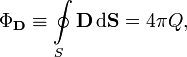




 Поэтому
Поэтому 
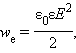
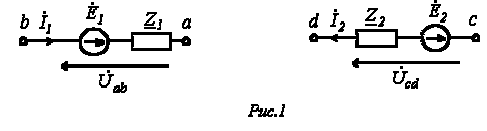
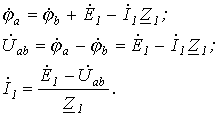



 ,
(2.11)
,
(2.11)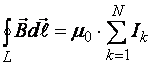 ,
(2.12)
,
(2.12)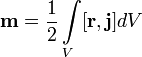 ,
,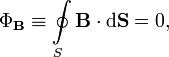
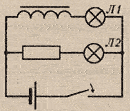 При
замыкании в эл.цепи нарастает ток, что
вызывает в катушке увеличение магнитного
потока, возникает вихревое эл.поле,
направленное против тока, т.е. в катушке
возникает ЭДС самоиндукции, препятствующая
нарастанию тока в цепи ( вихревое поле
тормозит электроны).
В результате Л1
загорается позже, чем
Л2.
При
замыкании в эл.цепи нарастает ток, что
вызывает в катушке увеличение магнитного
потока, возникает вихревое эл.поле,
направленное против тока, т.е. в катушке
возникает ЭДС самоиндукции, препятствующая
нарастанию тока в цепи ( вихревое поле
тормозит электроны).
В результате Л1
загорается позже, чем
Л2. При
размыкании эл.цепи ток убывает,
возникает уменьшение м.потока в
катушке, возникает вихревое эл.поле,
направленное как ток ( стремящееся
сохранить прежнюю силу тока) , т.е. в
катушке возникает ЭДС самоиндукции,
поддерживающая ток в цепи.
В
результате Л при выключении ярко
вспыхивает.
Вывод
в
электротехнике явление самоиндукции
проявляется при замыкании цепи (эл.ток
нарастает постепенно) и при размыкании
цепи (эл.ток пропадает не сразу).
При
размыкании эл.цепи ток убывает,
возникает уменьшение м.потока в
катушке, возникает вихревое эл.поле,
направленное как ток ( стремящееся
сохранить прежнюю силу тока) , т.е. в
катушке возникает ЭДС самоиндукции,
поддерживающая ток в цепи.
В
результате Л при выключении ярко
вспыхивает.
Вывод
в
электротехнике явление самоиндукции
проявляется при замыкании цепи (эл.ток
нарастает постепенно) и при размыкании
цепи (эл.ток пропадает не сразу). Индуктивность -
физ. величина, численно равная ЭДС
самоиндукции, возникающей в контуре
при изменении силы тока на 1Ампер за
1 секунду.
Также индуктивность можно
рассчитать по формуле:
Индуктивность -
физ. величина, численно равная ЭДС
самоиндукции, возникающей в контуре
при изменении силы тока на 1Ампер за
1 секунду.
Также индуктивность можно
рассчитать по формуле: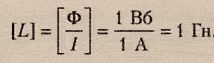
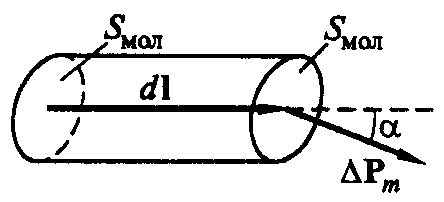 Наведенному
магнитному моменту Pm атома
(молекулы) можно сопоставить замкнутый
молекулярный ток Iмол с
площадью витка Sмол
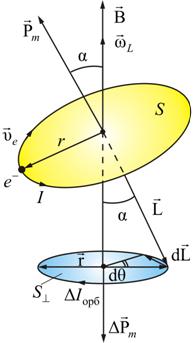
Наведенному
магнитному моменту Pm атома
(молекулы) можно сопоставить замкнутый
молекулярный ток Iмол с
площадью витка Sмол 
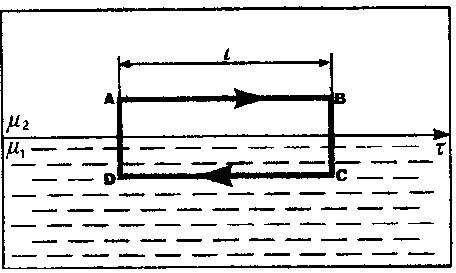 На
границе раздела двух
однородных магнетиков с относительными
магнитными проницаемостями 1
и 2
при отсутствии тока проводимости
характеристики магнитного поля
меняются.
На
границе раздела двух
однородных магнетиков с относительными
магнитными проницаемостями 1
и 2
при отсутствии тока проводимости
характеристики магнитного поля
меняются.  * Пример:
Если площадь поперечного сечения
участка цепи постоянна, то
* Пример:
Если площадь поперечного сечения
участка цепи постоянна, то

 где
первый член представляет собой сумму
собственных энергий всех токов, а
второй, называемый взаимной энергией
токов, определяется взаимосвязью
контуров системы (
где
первый член представляет собой сумму
собственных энергий всех токов, а
второй, называемый взаимной энергией
токов, определяется взаимосвязью
контуров системы (