11 Билет: Принцип относительности Галилея

Из формулы для ускорений следует, что если движущаяся система отсчета движется относительно первой без ускорения, то есть  , то ускорение   тела относительно обеих систем отсчета одинаково.

Поскольку в Ньютоновской динамике из кинематических величин именно ускорение играет роль (см.второй закон Ньютона), то, если довольно естественно предположить, что силы зависят лишь от относительного положения и скоростей физических тел (а не их положения относительно абстрактного начала отсчета), окажется, что все уравнения механики запишутся одинаково в любой инерциальной системе отсчета — иначе говоря, законы механики не зависят от того, в какой из инерциальных систем отсчета мы их исследуем, не зависят от выбора в качестве рабочей какой-либо конкретной из инерциальных систем отсчета. Также — поэтому — не зависит от такого выбора системы отсчета наблюдаемое движение тел (учитывая, конечно, начальные скорости). Это утверждение известно как принцип относительности Галилея, в отличие от Принципа относительности Эйнштейна

Иным образом этот принцип формулируется (следуя Галилею) так: если в двух замкнутых лабораториях, одна из которых равномерно прямолинейно (и поступательно) движется относительно другой, провести одинаковый механический эксперимент, результат будет одинаковым.

Требование (постулат) принципа относительности вместе с преобразованиями Галилея, представляющимися достаточно интуитивно очевидными, во многом следует форма и структура ньютоновской механики (и исторически также они оказали существенное влияние на ее формулировку). Говоря же несколько более формально, они накладывают на структуру механики ограничения, достаточно существенно влияющие на ее возможные формулировки, исторически весьма сильно способствовавшие ее оформлению.

Вид преобразований при коллинеарных осях^[4]

Если ИСО S движется относительно ИСО S' с постоянной скоростью   вдоль оси  , а начала координат совпадают в начальный момент времени в обеих системах, то преобразования Галилея имеют вид:

или, используя векторные обозначения,

(последняя формула остается верной для любого направления осей координат).

Как видим, это просто формулы для сдвига начала координат, линейно зависящего от времени (подразумеваемого одинаковым для всех систем отсчета).

Из этих преобразований следуют соотношения между скоростями движения точки и её ускорениями в обеих системах отсчета:

Преобразования Галилея являются предельным (частным) случаем преобразований Лоренца для малых скоростей  (много меньше скорости света).

12 Билет: Основы сто. Преобразования Лоренца и следствия из них.

В специальной теории относительности рассматриваются только инерциальные системы отсчета, т.е. такие, в которых выполняется закон инерции и скорость света в вакууме является универсальной постоянной.

Постулаты теории относительности

Первый постулат: законы физики имеют одинаковую форму во всех инерциальных системах отсчета. Это обобщение принципа относительности Ньютона на законы не только механики, но и всех других областей физики, носит название принципа относительности Эйнштейна.

Второй постулат: свет распространяется в вакууме с определенной скоростью c, не зависящей от скорости источника или наблюдателя. Согласно специальной теории относительности (СТО) скорость света в вакууме является абсолютной величиной, а такие абсолютные с точки зрения классической механики Ньютона понятия, как длина и время, стали относительными.

Из постулатов СТО следует, что скорость света в вакууме является предельно возможной. Никакой сигнал, никакое воздействие одного тела на другое не могут распространяться со скоростью, превышающей скорость света в вакууме.

Релятивистский закон сложения скоростей: если в неподвижной ситеме отсчета скорость тела и скорость движущейся системы отсчета направлены по одной прямой, то: 

г де u ' – скорость движения тела в движущейся системе отсчета; v – скорость движущейся системы K ' относительно неподвижной системы K;  u – скорость тела относительно неподвижной системы отсчета K (рис. 1).

Релятивистское замедление времени

Если t₀ – интервал времени между двумя событиями, происходящими в одной и той же пространственной точке, неподвижной относительно системы K ', а t – интервал времени между этими же событиями в системе K, то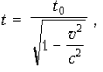 

где c – скорость света в вакууме. Время t₀, отсчитываемое по часам, покоящимся относительно данного тела, называется собственным временем. Оно всегда меньше времени, измеренного по движущимся часам: t₀ < t.

Релятивистское сокращение длины

Если l₀ – длина расположенного вдоль оси x ' стержня в системе K ', относительно которой он покоится, а l – длина этого стержня в системе K, относительно которой он движется вдоль оси x со скоростью v, то:

Поперечные размеры движущегося стержня не изменяются. Линейный размер стержня l₀ в той системе отсчета, где он покоится, называется собственной длиной. Эта длина максимальна: l₀ > l.

Импульс движущегося тела (релятивистский импульс): 

Полная энергия тела или системы тел: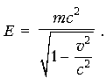 

Кинетическая энергия движущегося тела: 

где E₀ = mc² – энергия покоящегося тела.

Соотношение Эйнштейна

Энергия, импульс и масса. Для свободной частицы E² = p²c² + m²c⁴.

При изменении массы тела на Dm выделяется эквивалентная энергия E = mc².

Преобразования Лоренца

Пусть нам даны две системы отсчета k и k`. В момент t = О обе эти системы координат совпадают. Пусть система k` (назовем ее подвижной) движется так, что ось х` скользит по оси х, ось у` параллельна оси у, скорость v - скорость движения этой системы координат (рис. 109).

Точка М имеет координаты в системе k - х, у, z, a в системе k` - х`, у`, z`.

Преобразования Галилея в классической механике имеют вид:

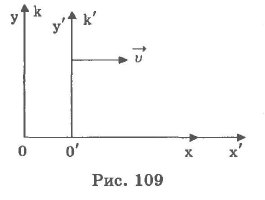
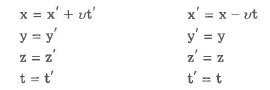
Преобразования координат, удовлетворяющие постулатам специальной теории относительности, называются преобразованиями Лоренца.

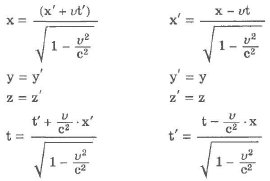
Впервые они (в несколько иной форме) были предложены Лоренцем для объяснения отрицательного эксперимента Майкельсона-Морли и для придания уравнениям Максвелла одинакового вида во всех инерциальных системах отсчета.

Эйнштейн вывел их независимо на основе своей теории относительности. Подчеркнем, что изменилась (по сравнению с преобразованием Галилея) не только формула преобразования координаты х, но и формула преобразований времени t. Из последней формулы непосредственно видно, как переплетены пространственная и временная координаты.

Следствия из преобразований Лоренца

Длина движущегося стержня.

Предположим, что стержень расположен вдоль оси х` в системе k` и движется вместе с системой k` со скоростью v.

Разность между координатами конца и начала отрезка в системе отсчета, в которой он неподвижен, называется собственной длиной отрезка. В нашем случае l₀ = х₂` - х<sub>1</sub>`, где х₂` - координата конца отрезка в системе k` и х/ - координата начала. Относительно системы k стержень движется. Длиной движущегося стержня принимают разность между координатами конца и начала стержня в один и тот же момент времени по часам системы k.

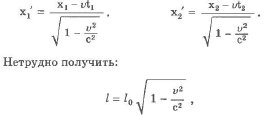
где l - длина движущегося стержня, l₀ - собственная длина стержня. Длина движущегося стержня меньше собственной длины.

Темп хода движущихся часов.

Пусть в точке х₀` движущейся системы координат k` происходит последовательно два события в моменты t/ и t₂. В неподвижной системе координат k эти события происходят в разных точках в моменты t₁ и t₂. Интервал времени между этими событиями в движущейся системе координат равен дельта t` = t<sub>2</sub>` - t₁`, а в покоящейся дельта t = t₂ - t₁.

На основании преобразования Лоренца получим:

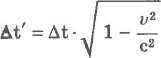
Интервал времени дельта t` между событиями, измеренный движущимися часами, меньше, чем интервал времени дельта t между теми же событиями, измеренный покоящимися часами. Это означает, что темп хода движущихся часов замедлен относительно неподвижных.

Время, которое измеряется по часам, связанным с движущейся точкой, называетсясобственным временем этой точки.

Относительность одновременности.

Из преобразований Лоренца следует, что если в системе k в точке с координатами x₁ и х₂происходили два события одновременно (t₁ = t₂ = t₀), то в системе k` интервал

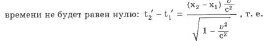
понятие одновременности - понятие относительное. События, одновременные в одной системе координат, оказались неодновременными в другой.

Относительность одновременности и причинность.

Из относительности одновременности следует, что последовательность одних и тех же событий в различных системах координат различна.

Не может ли случиться так, что в одной системе координат причина предшествует следствию, а в другой, наоборот, следствие предшествует причине?

Чтобы причинно-следственная связь между событиями имела объективный характер и не зависела от системы координат, в которой она рассматривается, необходимо, чтобы никакие материальные воздействия, осуществляющие физическую связь событий, происходящих в различных точках, не могли передаваться со скоростью, большей скорости света.

Таким образом, передача физического влияния из одной точки в другую не может происходить со скоростью, большей скорости света. При этом условии причинная связь событий носит абсолютный характер: не существует системы координат, в которой причина и следствие меняются местами.

13 билет. Элементы релятивности динамики.

С новыми пространственно-временными представлениями не согласуются при больших скоростях движения и законы механики Ньютона. Лишь при малых скоростях движения, когда справедливы классические представления о пространстве и времени, второй закон Ньютона (уравнение движения)

не меняет своей формы при переходе от одной инерциальной системы отсчета к другой (выполняется принцип относительности).

Но при больших скоростях движения этот закон в своей обычной (классической) форме несправедлив. Однако введенные в динамике основные понятия: энергия, импульс — имеют тот же физический смысл, лишь понятие массы в классической механике отличается от понятия массы в релятивистской динамике.

В природе существуют частицы, скорость которых равна скорости света. Это фотоны и различного типа нейтрино. Масса этих частиц равна нулю. Они не могут быть замедлены или ускорены. Поэтому во всех инерциальных системах отсчета их импульс и энергия не равны нулю. Такие частицы называются безмассовыми.

Энергия и импульс таких частиц связаны соотношениями Е = рс и Е² -р²с² = 0.    (9.5) Эти соотношения экспериментально подтверждены.

Однако для большинства частиц масса является одной из важнейших характеристик. Эти частицы называются массовыми. Скорость таких частиц   < с.

Массовая частица обладает собственной энергией: Е = mс².    (9.6) Согласно этой формуле тело обладает энергией и при скорости, равной нулю — энергией покоя.

Это замечательный результат. Любое тело уже только благодаря факту своего существования обладает энергией, которая пропорциональна его массе m. При превращениях элементарных частиц, обладающих массой покоя  , в частицы, у которых m = 0, их энергия покоя E₀ целиком превращается в кинетическую энергию вновь образовавшихся частиц. Этот факт является наиболее очевидным экспериментальным доказательством существования энергии покоя.

Во всех инерциальных системах отсчета импульс частицы и ее энергия связаны соотношением: Е² - р²с² = m²с⁴    (9.7) Так как величины m и с не меняются при переходе от одной системы отсчета к другой, то, следовательно, не меняется и значение Е² - р²с².

Выражение (9.7) преобразуется в уравнение (9.5) при m = 0, следовательно, оно справедливо также и для безмассовых частиц. Формула (9.7) является фундаментальным соотношением релятивистской механики.

Энергия частицы выражается через ее импульс следующим образом: Используя формулу (9.8), а также учитывая, что импульс частицы пропорционален ее скорости и энергии, получаем выражения для импульса и энергии частицы:  

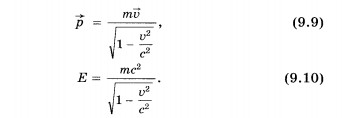
Последнее слагаемое — это выражение для кинетической энергии в классической механике.

Первое слагаемое в формуле (9.11) — это собственная энергия частицы.

Релятивистская энергия есть сумма собственной энергии частицы и релятивистской кинетической энергии Е_к: Е = mс² + Е_к.    (9.12) Из уравнений (9.10) и (9.12) получим выражение для релятивистской кинетической энергии массовой частицы

Обратим внимание на то, что так как подкоренное выражение в формуле (9.14) не зависит от выбора системы отсчета, то масса частицы не зависит от ее движения и остается одной и той же величиной во всех инерциальных системах отсчета.

Принцип соответствия. Законы динамики Ньютона и классические представления о пространстве и времени можно рассматривать как частный случай релятивистских законов при скоростях движения, много меньших скорости света.

Это проявление так называемого принципа соответствия, согласно которому любая теория, претендующая на более глубокое описание явлений и на более широкую сферу применимости, чем старая, должна включать последнюю как предельный случай.

Принцип соответствия впервые был сформулирован Нильсом Бором применительно к связи квантовой и классической теорий.

Импульс частицы и ее энергия зависят от выбора систе мы отсчета, масса же всегда остается постоянной. При скоростях много меньших скорости света релятивистские выражения для импульса и энергии переходят в выражснгия классической механики (принцип соответствия).

14 билет: Зако́н Куло́на — это закон, описывающий силы взаимодействия между точечными электрическими зарядами.

Был открыт Шарлем Кулоном в 1785 г. Проведя большое количество опытов с металлическими шариками, Шарль Кулон дал такую формулировку закона:

Модуль силы взаимодействия двух точечных зарядов в вакууме прямо пропорционален произведению модулей этих зарядов и обратно пропорционален квадрату расстояния между ними

Иначе: Два точечных заряда в вакууме действуют друг на друга с силами, которые пропорциональны произведению модулей этих зарядов, обратно пропорциональны квадрату расстояния между ними и направлены вдоль прямой, соединяющей эти заряды. Эти силы называются электростатическими (кулоновскими).

Важно отметить, что для того, чтобы закон был верен, необходимы:

точечность зарядов — то есть расстояние между заряженными телами много больше их размеров — впрочем, можно доказать, что сила взаимодействия двух объёмно распределённых зарядов со сферически симметричными непересекающимися пространственными распределениями равна силе взаимодействия двух эквивалентных точечных зарядов, размещённых в центрах сферической симметрии;

их неподвижность. Иначе вступают в силу дополнительные эффекты: магнитное поле движущегося заряда и соответствующая ему дополнительная сила Лоренца, действующая на другой движущийся заряд;

взаимодействие в вакууме.

Однако с некоторыми корректировками закон справедлив также для взаимодействий зарядов в среде и для движущихся зарядов.^[1]

В векторном виде в формулировке Ш. Кулона закон записывается следующим образом:

где   — сила, с которой заряд 1 действует на заряд 2;   — величина зарядов;   — радиус-вектор (вектор, направленный от заряда 1 к заряду 2, и равный, по модулю, расстоянию между зарядами —  );   — коэффициент пропорциональности. Таким образом, закон указывает, что одноимённые заряды отталкиваются (а разноимённые — притягиваются).

Напряженность электростатического поля - это силовая характеристика электростатического поля, численно равная силе, действующей на единичный положительный заряд.

Напряженность электростатического поля - векторная величина.

Напряженность электрического поля:

E = F/Qпробный

Напряженность электростатического поля (точечного заряда):

 

где r - расстояние от заряда Q, создающего поле, до точки поля, в которой определяется напряженность.

Единица напряженности - вольт на метр (В/м)

Электростатическое поле представляется графически силовыми линиями или линиями напряженности .

Принцип суперпозиции полей, также называемый принципом наложения, является условностью. Согласно которой некоторый сложный процесс взаимодействия между определённым числом объектов можно представить в виде суммы взаимодействий между отдельными объектами. Принцип суперпозиции применим лишь к тем системам,  которые описываются линейными уравнениями.  К примеру, электромагнитная волна распространяется в вакууме. Свойства вакуума не меняются при воздействии на него волны. И все эффекты, которые возникают при распространении этой волны, в случае если она негармоническая можно представить в виде суммы эффектов создаваемых отдельными гармониками. Этот же принцип применим и к полю создаваемому скоплением зарядов. Суммарное поле можно разделить на отдельные поля, которые создаются каждым зарядом в отдельности. И наоборот общее поле будет состоять из суммы полей отдельных зарядов.  Графически принцип суперпозиции полей можно представить в виде геометрической суммы векторов силы, которые действуют на пробный заряд, помещённый в поле точечных электрических зарядов.

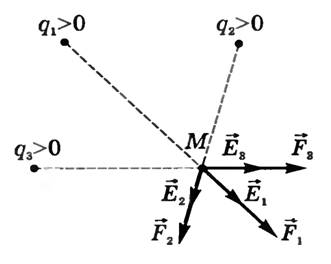
Рисунок 1 — графическое представление принципа суперпозиции

 

 Если поле создано простейшей совокупностью зарядов. Которая состоит из положительного и отрицательного зарядом находящихся на некотором расстоянии друг от друга. То результирующее поле в точке наблюдения находится, с помощью правила параллелограмма.

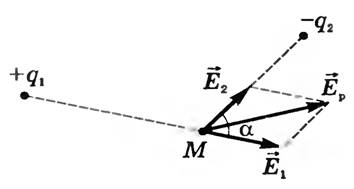
Рисунок  2 — иллюстрация к правилу параллелограмма

 

 В случае если поле создается заряженным телом, имеющим протяжённые линейные размеры. То его необходимо мысленно разбить на небольшие участки, действие которых можно считать аналогичным действию точечных зарядов. И провести геометрическое суммирование полей этих отдельных участков. Таким образом, применив принцип суперпозиции полей к массивному телу.  Принцип суперпозиции не является фундаментальным законом или постулатом. Он всего лишь вытекает из других принципов, например в электростатике основой для принципа суперпозиции являются уравнения Максвелла. Так как они линейны для вакуума это и дает основу для применения этого принципа.  Но скажем если рассматривать в качестве среды не вакуум. А скажем ферромагнетик, то линейность в данной среде отсутствует. Так как намагниченность ферромагнетика определяется кривой намагниченности. Которая конечно и имеет некоторый участок обладающий линейностью, но в целом имеет и участок насыщения с резко выраженной нелинейностью. И принцип суперпозиции в данном случае не применим.  Также нельзя применять принцип суперпозиции и к взаимодействию атомов и молекул между собой. Например, если взять два атома, у которых электроны находятся во взаимодействии. И поднести к ним третий такой же атом. Часть электронов от первых двух атомов притянется и вступит во взаимодействие с третьим атомом. То есть первоначальное распределение энергии в системе измениться. Изначальная сила взаимодействия между электронами и ядрами первых двух атомов уменьшится. То есть третий атом влияет не только на электроны, но и на ядра атомов.

15 билет. Поток вектора напряженности электростатического поля.: Число линий вектора E, пронизывающих некоторую поверхность S, называется потоком вектора напряженности N_E.

Для вычисления потока вектора E необходимо разбить площадь S на элементарные площадки dS, в пределах которых поле будет однородным (рис.13.4).

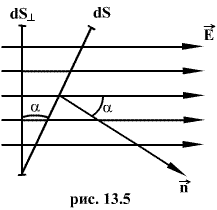
Поток напряженности через такую элементарную площадку будет равен по определению(рис.13.5).

где   - угол между силовой линией и нормалью   к площадке dS;   - проекция площадки dS на плоскость, перпендикулярную силовым линиям. Тогда поток напряженности поля через всю поверхность площадки S будет равен

(13.4)

Так как   , то

(13.5)

где   - проекция вектора   на нормаль и к поверхности dS.

графическое изображение электрического поля. Метод графического изображения электрического поля был предложен английским физиком Майклом Фарадеем. Суть метода заключается в том, что на чертеже изображаются непрерывные линии, которые называют линиями напряженности, или силовыми линиями.

Правило построения линий напряженности заключается в том, что касательные к ним в каждой точке чертежа совпадают с направлением вектора напряженности поля в изображаемой точке.

Таким образом, силовые линии имеют то же направление, что и напряжённость поля и не пересекаются, так как в каждой точке электрического поля вектор E имеет лишь одно направление.

С помощью силовых линий можно дать количественную характеристику напряжённости электрического поля. Для этого густота, или плотность, силовых линий выбирается пропорционально модулю вектора напряженности. Плотность силовых линий определяется как число линий, пронизывающих единичную поверхность в направлении, перпендикулярном к этой поверхности.

Изображение силовых линий позволяет получать картину поля, которая наглядно показывает, чему равна напряженность в разных частях поля и как она изменяется в пространстве

16 билет. Теорема Острогадского-Гаусса для электрического поля. Общая формулировка: Поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду.

СГС	СИ

где

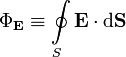 — поток вектора напряжённости электрического поля через замкнутую поверхность  .

 — полный заряд, содержащийся в объёме, который ограничивает поверхность  .

 — электрическая постоянная.

Данное выражение представляет собой теорему Гаусса в интегральной форме.

Замечание: поток вектора напряжённости через поверхность не зависит от распределения заряда (расположения зарядов) внутри поверхности.

В дифференциальной форме теорема Гаусса выражается следующим образом:

СГС	СИ

Здесь   — объёмная плотность заряда (в случае присутствия среды — суммарная плотность свободных и связанных зарядов), а   — оператор набла.

Теорема Гаусса может быть доказана как теорема в электростатике исходя из закона Кулона (см. ниже). Формула однако также верна в электродинамике, хотя в ней она чаще всего не выступает в качестве доказываемой теоремы, а выступает в качестве постулируемого уравнения (в этом смысле и контексте ее логичнее называть законом Гаусса^[2].

17 билет: Потенциальная энергия. Потенциал.

 работа не зависит от пути, по которому перемещался в электростатическом поле пробный заряд   , и зависит только от положений точек “а” и “b”. Такое поле называется потенциальным. Поэтому работа, очевидно, равна убыли потенциальной энергии W этого заряда

Перенесем пробный заряд на бесконечность. Напряженность поля Е на бесконечности принимается равной нулю, следовательно   . Но так как   , то второе слагаемое тоже будет равно нулю и тогда

Электромагнитный потенциал — четырёхмерная величина (4-вектор), характеризующая электромагнитное поле. Играет фундаментальную роль как в классической, так и в квантовой электродинамике.

Электромагнитный потенциал можно представить состоящим из потенциалов электромагнитного поля φ и A, рассматриваемых в традиционной трехмерной формулировке электродинамики как отдельные величины, определяющие вместе электромагнитное поле:

скалярного (в трёхмерном смысле) потенциала φ, вместе с A определяющего электрическое поле;

в частности, для постоянных полей или при условиях, позволяющих пренебречь быстротой их изменения, скалярный потенциал выступает как

Электростатический потенциал — через который электростатическое поле определяется полностью;

и векторного потенциала A — трёхмерного вектора, полностью определяющего магнитное поле, а электрическое поле определяющего вместе с φ.

Рассмотрим однородное электрическое поле, в котором заряд + q перемещается из точки 1 с координатой  , в точку 2 с координатой  под действием кулоновской силы вдоль линии напряженности (рис.1.6).

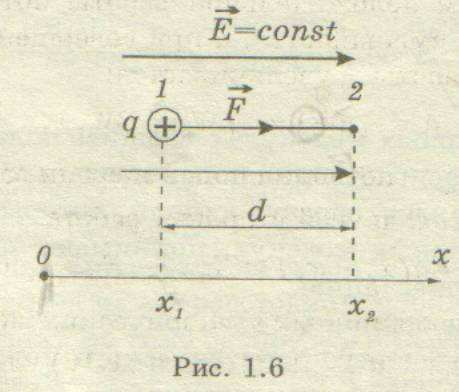
Работа этой силы (1.12)

где  . При перемещении заряда между этими же точками по любой криволинейной траектории будет совершена такая же работа. Работа перемещения заряда в электростатическом поле не зависит от формы траектории движения заряда, а зависит от положения в этом поле начальной и конечной точек перемещения. Поля, обладающие таким свойством, называются потенциальными, т.е. электростатические поля являются потенциальными. Перенесем теперь тот же заряд из точки 2 в точку 1. Так как теперь сила направлена против перемещения, то работа                                 (1.13) Суммарная же работа перемещения заряда по замкнутой траектории будет равна нулю:                             (1.14) Согласно закону сохранения энергии работа перемещения заряда ^ в электростатическом поле равна изменению его потенциальной энергии, взятому со знаком минус. Связано это с тем, что при совершении полем положительной работы потенциальная энергия уменьшается, а при совершении отрицательной работы -увеличивается:                          (1.15) где   - потенциальные энергии заряда q в точках 1 и 2. С другой стороны, работа              (1.16) где Е ~ напряженность поля, а  , и   - координаты точек поля 1 и 2. Из (1.15) и (1.16) следует:                          (1.17)  Таким образом, величина потенциальной энергии заряда в электростатическом поле .             (1.18) Разные заряды в точке с координатой хобладают разной потенциальной энергией. Однако, отношение значения потенциальной энергии к величине соответствующего заряда есть величина постоянная, равная величине потенциальной энергии единичного заряда, находящегося в данной точке поля. Эта величина называется потенциалом поля в данной точке:                                               (1.19)