7 Билет: Работа силы

Понятие “работа“ как физическая величина во всех энциклопедиях, справочниках и учебниках раскрывается как понятие “работа силы“ при описании прямолинейной механической формы движения. Правда, в физике применяется также и понятие “работа поля“, которое трактуется, как “работа сил поля“.  В БСЭ работа силы определяется, как “мера действия силы, зависящая от численной величины и направления силы и от перемещения точки её приложения“. В метрологическом справочнике А.Чертова (1990) определение работы силы присутствует в виде словесной формулировки определяющего уравнения для элементарной работы силыF на элементарном перемещении dr без раскрытия ее физического содержания:  dA = F dr . ( 1 )  На конечном перемещении A = Fr. Оба вышеприведенных определения относятся к механическим системам.  Учебник по физике И.Савельева (2005) так определяет физическое содержание работы силы: “Работа результирующей всех сил, действующих на частицу, идет на приращение кинетической энергии частицы“. Однако в следующем параграфе этого же учебника работа силы трактуется уже, как причина приращения потенциальной энергии, из чего можно сделать вывод, что работа сил идет на приращение любого вида энергии. Что именно понимается под видами энергии, показано на странице, посвященной формам и видам энергии.  Рассмотрим две формы записи главного определяющего уравнения, приведенные на странице, посвященной обобщенному уравнению состояния:  dW = U dq  ( 2 )        и       U dq = dW , ( 3 )  где dW − энергетическое воздействие на систему, dq − приращение координаты состояния системы, U −динамическое воздействие на систему. Там же было показано, что главное определяющее уравнение в форме (3)соответствует принципу причинности, и именно оно должно применяться во всех случаях внешнего энергетического воздействия dW на систему.  Уравнение (2) совпадает с уравнением (1) для работы силы dA, если в качестве координаты состояния dq в механической прямолинейной форме движения принять перемещение dr, а в качестве динамического воздействия Uпринять силу F. Но уравнение (2) не соответствует принципу причинности. Из чего следует, что работа силы dA, если ее определять по уравнению (1), не является энергетическим воздействием dW на механическую систему.  Чтобы в механической прямолинейной форме движения соблюдался принцип причинности, уравнение (1) должно быть заменено уравнением с перестановкой левой и правой частей  F dr = dА . ( 4 )  При применении записи, аналогичной уравнению (3), понятие “работа“ можно применять не только в прямолинейной форме движения и можно говорить не только о работе силы. С таким же успехом и с той же размерностью можно говорить и о работе вращающего момента M при вращательной форме движения, и о работе перепада давленийΔp при гидравлической объёмной форме движения, и о работе в других формах движения. То есть уравнение (2) можно записать также в виде:  M dφ = dА   ( 5 )      или     Δp dV = dА    , ( 6 )  где dφ − элементарный угол поворота; dV − элементарное перемещение объёма.  На странице, посвященной формам движения, показано, что выбор формы движения определяется выборомкоординаты состояния. И уж по координате состояния определяется вид динамического воздействия. В приведенных выше примерах выбор в качестве координаты состояния перемещения предопределил то, что в качестве динамического воздействия появилась сила, выбор угла поворота предопределил появление вращающего момента, выбор объемного перемещения предопределил появление перепада давлений. Именно такая причинно-следственная цепочка имеет место в природе, хотя при изучении физики по современной методологии складывается впечатление, что всё наоборот.  Лишь при рассмотрении понятия “работа сил поля“ причина и следствие меняются местами: силы взаимодействия зарядов поля становятся причиной, а работа этих сил − следствием. И поэтому данной ситуации соответствует главное определяющее уравнение в форме (2).

Если работаA=Fs=mas, можно выразить перемещение и ускорение через скорость. При равноускоренном одномерном движенииa=(v_к-v_н)/t,s=v_cpt=(v_к+v_н)(v_к-v_н)/2a=(v_к²-v_н²)/2a.ПоэтомуA= ½(mv_к²-mv_н²)=E_{к н}-E_кк=∆Е_к. Величина ½mv²называется кинетической энергией, т.е.энергией движения (от греч.kinema, Е_к может также обозначаться К или Т).

Вывод, что работа результирующей силы равна изменению кинетической энергии тела, справедлив и при изменении ускорения и сил, не только для равноускоренного прямолинейного движения, и известен как теорема об изменении кинетической энергии.

Это понятие связано с законом сохранения «силы» или энергии.

8 билет: Кинетическая энергия вращающегося тела. Кинетическая энергия тела при плоском движении. Кинетическая энергия тела, движущегося произвольным образом, равна сумме кинетических энергий всех n материальных точек па которые это тело можно разбить:

Если тело вращается вокруг неподвижной оси с угловой скоростью  , то линейная скорость i-ой точки равна  , где  , - расстояние от этой точки до оси вращения. Следовательно.

(5.11)

где   - момент инерции тела относительно оси вращения.

В общем случае движение твердого тела можно представить в виде суммы двух движений - поступательного со скоростью, равной скорости   центра инерции тела, и вращения с угловой скоростью   вокруг мгновенной оси, проходящей через центр инерции. При этом выражение для кинетической энергии тела преобразуется к виду

(5.12)

где   - момент инерции тела относительно мгновенной оси вращения, проходящей через центр инерции. кинетическая энергия при плоском движении

Плоским (плоскопараллельным) называется такое движение, при котором все точки тела движутся в параллельных плоскостях. Представим плоское движение тела как поступательное движение со скоростью  , некоторой точки 0 в нем и вращения вокруг оси, проходящей через эту же точку и перпендикулярной   с угловой скоростью  .

В этом случае скорость i-той материальной точки тела определяется формулой

.

Кинетическая энергия i- той материальной точки равна

или

.

Просуммировав по всем материальным точкам, получим

или  , (12)

где М - полная масса тела,   - радиус-вектор центра масс,   - момент инерции тела относительно оси, проходящей через точку О.

Если в качестве точки О взять центр масс тела С, то   и формула (12) упрощается: . (13)

Таким образом, если разбить плоское движение тела на поступательное со

скоростью центра масс V_c и вращательное с угловой скоростью вокруг оси, проходящей через центр масс тела, то кинетическая энергия распадается на два независимых слагаемых, одно из которых определяется только скоростью центра масс V_c, а другое - угловой скоростью .

Из (13) следует, что при вращении тела относительно оси z, проходящей через центр масс С, его кинетическая энергия  . (14)

9 билет. консервативные силы. Потенциальная энергия: В физике консервати́вные си́лы (потенциальные силы) — силы, работа которых не зависит от формы траектории (зависит только от начальной и конечной точки приложения сил)^[1]. Отсюда следует определение: консервативные силы — такие силы, работа которых по любой замкнутой траектории равна 0.

Если в системе действуют только консервативные силы, то механическая энергия системы сохраняется.

Для консервативных сил выполняются следующие тождества:

 — ротор консервативных сил равен 0;

 — работа консервативных сил по произвольному замкнутому контуру равна 0;

 — консервативная сила является градиентом некой скалярной функции  , называемой силовой. Эта функция равна потенциальной энергии   взятой с обратным знаком. Соответственно,   и   связаны соотношением

Таким образом, потенциальная сила всегда направлена против направления возрастания потенциальной энергии.

В школьной программе по физике силы разделяют на консервативные и неконсервативные. Примерами консервативных сил являются: сила тяжести, сила упругости, сила кулоновского (электростатического) взаимодействия. Примерами неконсервативных сил являются сила трения и сила сопротивления среды.

Потенциальная энергия   — скалярная физическая величина, характеризующая способность некого тела (или материальной точки) совершать работу за счет своего нахождения в поле действия сил. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы^[1]. Термин «потенциальная энергия» был введен в XIX веке шотландским инженером и физиком Уильямом Ренкином.

Единицей измерения энергии в СИ является Джоуль.

Потенциальная энергия принимается равной нулю для некоторой конфигурации тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной конфигурации называется нормировкой потенциальной энергии.

Корректное определение потенциальной энергии может быть дано только в поле сил, работа которых зависит только от начального и конечного положения тела, но не от траектории его перемещения. Такие силы называются консервативными.

Также потенциальная энергия является характеристикой взаимодействия нескольких тел или тела и поля.

Любая физическая система стремится к состоянию с наименьшей потенциальной энергией.

Потенциальная энергия упругой деформации характеризует взаимодействие между собой частей тела

10 билет. Закон сохранения механической энергии: Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только посредством сил тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком: 

A = –(Eр2 – Eр1).

По теореме о кинетической энергии эта работа равна изменению кинетической энергии тел (см. §1.19): 

Следовательно 

или

Ek1 + Ep1 = Ek2 + Ep2.

Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной.

Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона. Сумму E = E_k + E_p называют полной механической энергией. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии.

Пример применения закона сохранения энергии – нахождение минимальной прочности легкой нерастяжимой нити, удерживающей тело массой m при его вращении в вертикальной плоскости (задача Х. Гюйгенса). Рис. 1.20.1 поясняет решение этой задачи.

Рисунок 1.20.1. К задаче Христиана Гюйгенса.   – сила натяжения нити в нижней точке траектории

Закон сохранения энергии для тела в верхней и нижней точках траектории записывается в виде: 

Обратим внимание на то, что сила   натяжения нити всегда перпендикулярна скорости тела; поэтому она не совершает работы.

При минимальной скорости вращения натяжение нити в верхней точке равно нулю и, следовательно, центростремительное ускорение телу в верхней точке сообщается только силой тяжести: 

Из этих соотношений следует: 

Центростремительное ускорение в нижней точке создается силами   и   направленными в противоположные стороны: 

Отсюда следует, что при минимальной скорости тела в верхней точке натяжение нити в нижней точке будет по модулю равно 

F = 6mg.

Прочность нити должна, очевидно, превышать это значение.

Очень важно отметить, что закон сохранения механической энергии позволил получить связь между координатами и скоростями тела в двух разных точках траектории без анализа закона движения тела во всех промежуточных точках. Применение закона сохранения механической энергии может в значительной степени упростить решение многих задач.

В реальных условиях практически всегда на движущиеся тела наряду с силами тяготения, силами упругости и другими консервативными силами действуют силы трения или силы сопротивления среды.

Сила трения не является консервативной. Работа силы трения зависит от длины пути.

Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание).

При любых физических взаимодействиях энергия не возникает и не исчезает. Она лишь превращается из одной формы в другую.

Этот экспериментально установленный факт выражает фундаментальный закон природы – закон сохранения и превращения энергии.

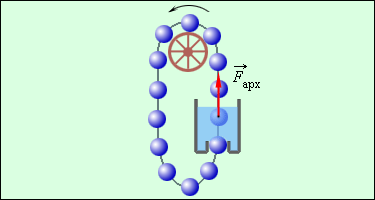
Одним из следствий закона сохранения и превращения энергии является утверждение о невозможности создания «вечного двигателя» (perpetuum mobile) – машины, которая могла бы неопределенно долго совершать работу, не расходуя при этом энергии (рис. 1.20.2).

Рисунок 1.20.2. Один из проектов «вечного двигателя». Почему эта машина не будет работать?

История хранит немалое число проектов «вечного двигателя». В некоторых из них ошибки «изобретателя» очевидны, в других эти ошибки замаскированы сложной конструкцией прибора, и бывает очень непросто понять, почему эта машина не будет работать. Бесплодные попытки создания «вечного двигателя» продолжаются и в наше время. Все эти попытки обречены на неудачу, так как закон сохранения и превращения энергии «запрещает» получение работы без затраты энергии.