2. Определение межосевого расстояния аw (мм) из условия прочности по контактным напряжениям

, (10)

где Т₂ – номинальный вращающий момент на колесе, Н·м;

u – передаточное число;

Ψ_ba – коэффициент ширины зубчатого венца относительно межосевого расстояния (Ψ_ba = b/a_w) (см. 2.1);

К_Нβ – коэффициент концентрации нагрузки при расчете контактных напряжений (см. 2.2);

К_Нv – коэффициент динамичности нагрузки при расчете контактных напряжений (см. 2.3);

К_Нα – коэффициент неравномерности нагружения зубьев (см. 2.4);

К_а – вспомогательный коэффициент (см. 2.5);

- для прямозубых передач;

- для косозубых передач;

в формуле (10) знак «+» - для внешнего зацепления, «-» - для внутреннего зацепления.

2.1. Коэффициент ширины зубчатого венца относительно межосевого расстояния выбирается разработчиком. При этом целесообразно использовать рекомендации, выработанные практикой проектирования закрытых передач при различном расположении зубчатых колес относительно опор:

Ψ_ba = 0,30…0,50 – симметричном;

Ψ_ba = 0,25…0,40 – асимметричном;

Ψ_ba = 0,20…0,25 – консольном;

Ψ_ba = 0,40…0,60 – для передачи шевронными колесами.

Открытые передачи конструируют узкими с коэффициентом ширины Ψ_ba = 0,1…0,2.

2.2. Коэффициент концентрации К_Нβ нагрузки можно вычислять с помощью приближенных (эмпирических) формул в зависимости от коэффициента ширины зубчатого венца относительно делительного диаметра шестерни Ψ_bd = b/d₁ и твердости поверхности зубьев. Формулы приведены в таблице 2.2.1.

Таблица 2.2.1

Коэффициент концентрации нагрузки кНβ

	1,0 < Ψbd < 1,6
Размещение шестерни относительно опор	HRC ≥ 35	HRC < 35
Консольное	1,0 + 0,766 Ψbd	1,0 + 0,3466 Ψbd
Асимметричное	1,0 + 0,275 Ψbd	1,0 + 0,1275 Ψbd
Симметричное	1,0 + 0,1388 Ψbd	1,0 + 0,0086 Ψbd
	Ψbd < 1,0
Консольное	1,0 + 0,766 Ψbd	1,0 + 0,4466 Ψbd
Асимметричное	1,0 + 0,275 Ψbd	1,0 + 0,1 Ψbd
Симметричное	1,0 + 0,052 Ψbd	1,0 + 0,0373 Ψbd

Примечние: коэффициент ширины зубчатого венца относительно делительного диаметра шестерни можно вычислить по зависимости Ψ_bd = 0,5 Ψ_ba(u ± 1).

Кроме указанных формул для определения коэффициента концентрации нагрузки можно использовать графики, представленные на рисунке 6.

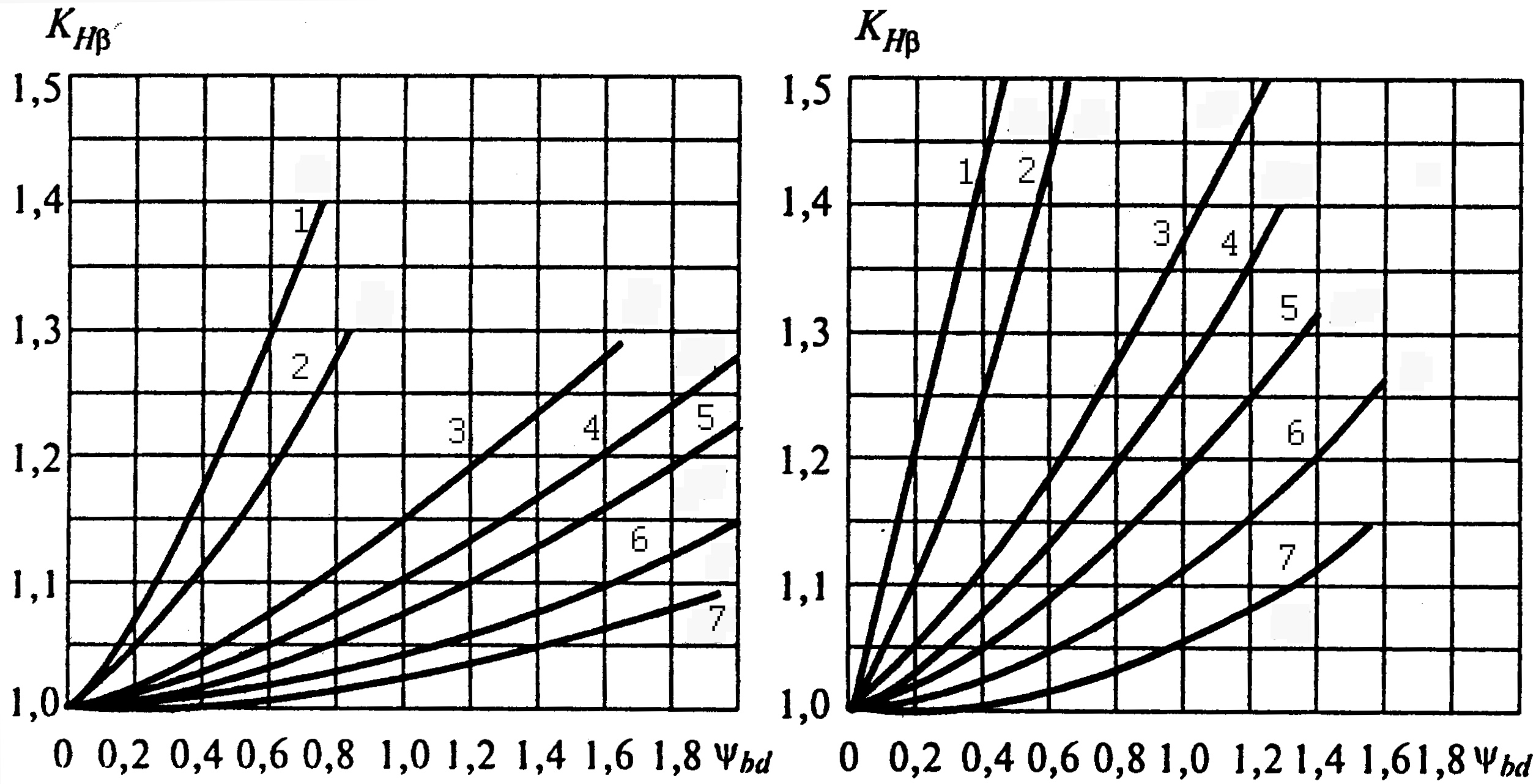
НВ ≤ 350 НВ > 350

Рис. 6. Графики для определения коэффициента концентрации нагрузки К_Нβ

(номера кривых соответствуют схемам, изображенным на рисунке 7)

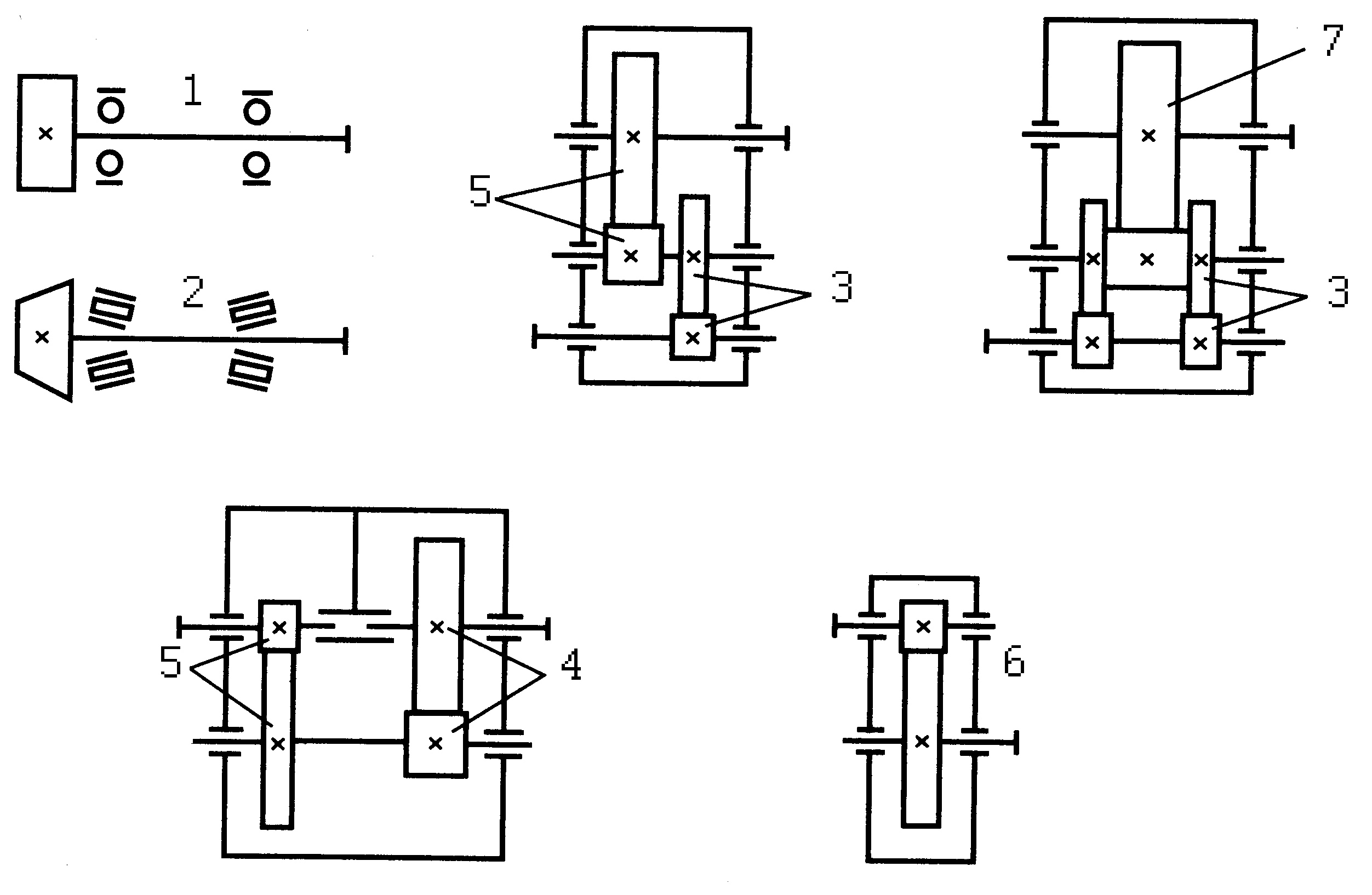
Рис. 7. Схемы расположения шестерен и колес на валах

2.3. Коэффициент динамичности нагрузки на этапе проектировочного расчета обычно принимают равным К_Нv = 1,0.

2.4. Коэффициент неравномерности нагружения зубьев на этапе проектировочного расчета обычно принимают равным: для косозубых передач К_Нα = 1,05, для прямозубых передач К_Нα = 1.

2.5. Вспомогательный коэффициент К_а = 430 для косозубых и шевронных передач, К_а = 495 для прямозубых передач (ГОСТ 21354 – 87).

Полученную величину межосевого расстояния следует округлить либо до ближайшего значения из нормального ряда R_а40 (табл. 2.2.2), либо до значения, оканчивающегося на ноль.

Таблица 2.2.2

Нормальные линейные размеры, мм (из ГОСТ 6636 – 69)

3,2	5,6	10	18	32	56	100	180	320	560
3,4	6,0	10,5	19	34/35	60/62	105	190	340	600
3,6	6,3	11	20	36	63/65	110	200	360	630
3,8	6,7	11,5	21	38	67/70	120	210	380	670
4,0	7,1	12	22	40	71/72	125	220	400	710
4,2	7,5	13	24	42	75	130	240	420	750
4,5	8,0	14	25	45/47	80	140	250	450	800
4,8	8,5	15	26	48	85	150	260	480	850
5,0	9,0	16	28	50/52	90	160	280	500	900
5,3	9,5	17	30	53/55	95	170	300	530	950

Примечание: под косой чертой приведены размеры посадочных мест под подшипники качения.

3. Определение ширины колеса

(11)

4. Определение ширины шестерни

Для компенсации возможных ошибок осевого положения шестерни относительно колеса, в качестве значения ширины шестерни b₁ принимается величина, превышающая на несколько миллиметров ширину колеса b₂:

(12)

5. Предварительное значение делительного диаметра колеса

(13)

6. Определение ориентировочного значения модуля из расчета прочности по напряжениям изгиба

, (14)

где K_m – поправочный коэффициент (см. 6.1);

K_F – коэффициент расчетной нагрузки (см. 6.2);

[σ_F]_min – меньшее из значений [σ_F]₁ и [σ_F]₂;

(Т₂ – в Н·м; b₂ и d₂ – в мм; [σ_F]_min – в МПа).

6.1. Поправочный коэффициент:

K_m = 3,5 для косозубых и шевронных передач, K_m = 5,0 для прямозубых цилиндрических передач.

6.2. Коэффициент расчетной нагрузки K_F = K_FβK_Fv,

где K_Fβ – коэффициент концентрации нагрузки при расчете напряжений изгиба (см. 6.2.1);

K_Fv – коэффициент динамичности нагрузки (см. 6.2.2).

6.2.1. Коэффициент концентрации нагрузки K_Fβ можно вычислять с помощью приближенных (эмпирических) формул в зависимости от коэффициента ширины зубчатого венца относительно делительного диаметра шестерни Ψ_bd = b/d₁ и твердости поверхности зубьев. Формулы приведены в таблице 2.6.1.

Таблица 2.6.1