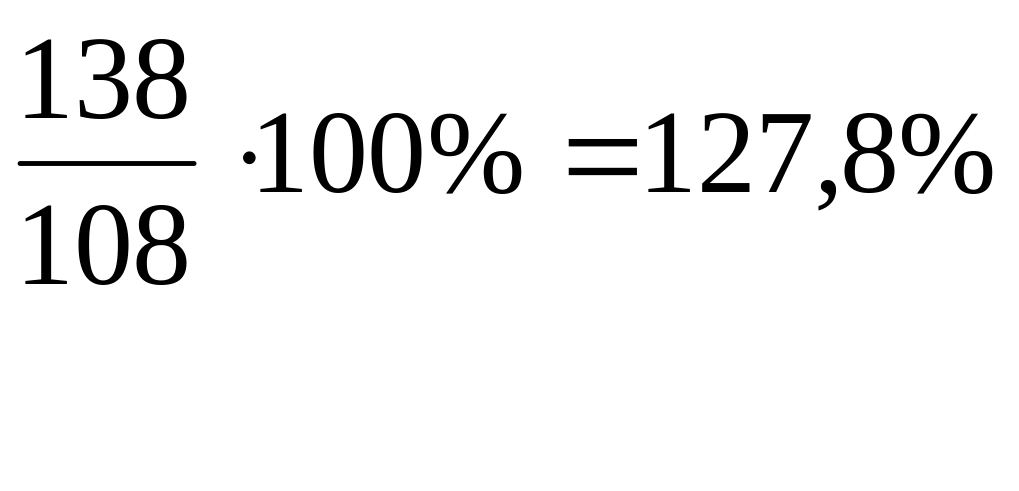Производство сахара-песка

	январь	февраль	март	апрель
Объем производства, тыс. т	108	138	131	206

Рассчитаем относительные показатели динамики с переменной и постоянной базой сравнения:

Переменная база сравнения (цепные показатели)	Постоянная база сравнения (базисные показатели)

Относительные показатели динамики с переменной и постоянной базой сравнения взаимосвязаны между собой следующим образом: произведение всех относительных показателей с переменной базой равно относительному показателю с постоянной базой за исследуемый период. Так, для рассчитанных показателей (предварительно переведя их из процентов в коэффициенты) получим:

1,278 • 0,949 • 1,573 = 1,907 или 190,7% .

Относительные показатели плана и реализации плана

Все субъекты финансово-хозяйственной деятельности (от небольших индивидуальных частных предприятий и до крупных корпораций) в той или иной степени осуществляют как текущее, так и стратегическое планирование, а также сравнивают реально достигнутые результаты с ранее намеченными. Для этой цели используются относительные показатели плана (ОПП) и реализации плана (ОПРП).

Пример. Предположим, оборот торговой фирмы в 1996 г. составил 2,0 млрд. руб. Исходя из проведенного анализа складывающихся на рынке тенденций руководство фирмы считает реальным в следующем году довести оборот до 2,8 млрд. руб. В этом случае относительный показатель плана, представляющий собой отношение планируемой величины к фактически достигнутой, составит 140% . Предположим, что фактический оборот фирмы за 1997 г. составил 2,6 млрд. руб. Тогда относительный показатель реализации плана, определяемый как отношение фактически достигнутой величины к ранее планированной, составит 92,9%

Между относительными показателями плана, реализации плана и динамики существует следующая взаимосвязь:

ОПП  ОПРП = ОПД.

В нашем примере: 1,40  0,929 = 1,3

Основываясь на этой взаимосвязи, по любым двум известным величинам, при необходимости всегда можно определить третью неизвестную величину.

Относительный показатель структуры (ОПС) представляет собой соотношение структурных частей изучаемого объекта и их целого. Выражается ОПС в долях единицы или в процентах. Рассчитанные величины, соответственно называемые долями или удельными весами, показывают, какой долей обладает или какой удельный вес имеет та или иная часть в общем итоге.

Пример. Рассмотрим табл. 3.2. Рассчитанные в последней графе табл. 3.2 проценты представляют собой относительные показатели структуры (в данном случае - удельные веса). Сумма всех удельных весов всегда должна быть строго равна 100%.

Таблица 3.2

Структура валового внутреннего продукта РФ в 1 квартале 2000 г.

	Объем
	Трлн. руб.	% к итогу
ВВП – всего В том числе: Производство товаров Производство услуг Чистые налоги на продукты	508 185,4 227,9 44,7	100 36,5 54,7 8,8

Относительный показатель координации (ОПК) представляет собой отношение одной части совокупности к другой части этой же совокупности. При этом в качестве базы сравнения выбирается та часть, которая имеет наибольший удельный вес или является приоритетной с экономической, социальной или какой-либо другой точки зрения. В результате получают, во сколько раз данная часть боль­ше базисной, или сколько процентов от нее составляет, или сколько единиц данной структурной части приходится на 1 единицу (иногда- на 100, 1000 и т. д. единиц) базисной структурной части. Так, на основе данных приведенной выше табл. 3.2 мы можем вычислить, что на каждый триллион рублей произведенных товаров приходится 1,50 трлн. руб. произведенных услуг и 0,24 трлн. руб. чистых налогов на .

Относительный показатель интенсивности (ОПИ) характеризует степень распространения изучаемого процесса или явления и представляет собой отношение исследуемого показателя к размеру присущей ему среды. Данный показатель получают сопоставлением разноименных, но взаимосвязанных в своем развитии величин. Поэтому наиболее часто он представляет собой именованную величину, но может быть выражен и в процентах, промилле, продецимилле.

Обычно относительный показатель интенсивности рассчитывается в тех случаях, когда абсолютная величина оказывается недостаточной для формулировки обоснованных выводов о масштабах явления, его размерах, насыщенности, плотности распространения. Например, для определения уровня обеспеченности населения легковыми автомобилями рассчитывается число автомашин, приходящихся на 100 семей, для определения плотности населения рассчитывается число людей, приходящихся на 1 км².

Пример. На начало мая 1996 г. численность граждан, состоящих на учете в службе занятости, составляла 3064 тыс. человек, а число заявленных предприятиями вакансий - 309 тыс. Отсюда следует, что на каждых 100 незанятых приходилось 10 свободных мест .

Разновидностью относительных показателей интенсивности являются относительные показатели уровня экономического развития, характеризующие производство продукции в расчете на душу населения и играющие важную роль в оценке развития экономики государства. Так как объемные показатели производства по своей природе являются интервальными, а показатель численности населения - моментным, в расчете используют среднюю за период численность населения (например, среднегодовую).

Пример. Рассматривая лишь абсолютный размер ВВП России в 1 квартале 1996 г. (508 трлн. руб.), трудно оценить или «почувствовать» эту величину. Для того чтобы на основе данной цифры сделать вывод об уровне развития экономики, необходимо сопоставить ее со среднеквартальной численностью населения страны (148,1 млн. чел.), которая в простейшем случае рассчитывается как полусумма численности населения на начало и на конец квартала. В результате размер ВВП на душу населения состава 3.43 млн. руб. .

Относительный показатель сравнения (ОПС) представляет собой соотношение одного и того же абсолютного показателя, характеризующего разные объекты (предприятия, фирмы, районы, области, страны и т. п.).

Пример. На начало 1996 г. операции с ГКО - ОФЗ проводили в Москве 108, в Новосибирске 16 и в Санкт-Петербурге 13 официальных дилеров. Таким образом, в Москве дилеров было в 6,8 раза больше, чем в Новосибирске , и в 8,3 раза больше, чем в Санкт-Петербурге .

Наиболее распространенной формой статистических показателей, используемой в социально-экономических исследованиях, является средняя величина, представляющая собой обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени.

Определить среднюю во многих случаях удобнее через исходное соотношение средней (ИСС).

Для каждого показателя, используемого в социально-экономическом анализе, можно составить только одно истинное исходное соотношение средней. Однако от того, в каком виде представлены исходные данные, зависит, каким именно образом исходное соотношение средней будет реализовано. Расчет большинства конкретных статистических показателей основан на использовании средней агрегатной, средней арифметической или средней гармонической. Эти виды средней мы и рассмотрим в данной главе. Однако необходимо иметь в виду, что в анализе динамики для расчета среднего темпа роста используется средняя геометрическая; ряд статистических показателей, характеризующих вариацию и взаимосвязь, базируется на средней квадратической и степенных средних более высоких порядков.

Все средние, за исключением средней агрегатной, могут рассчитываться в двух вариантах - как взвешенные или невзвешенные.

Пример. По данным табл. 3.3 рассчитаем среднюю заработную плату в целом по трем предприятиям АО.

Таблица 3.3