21. Ламинарные пламенна. Химическое превращение в пламени.

Известны два различных режима распространения волны реакции в про­странстве — со сверхзвуковой и дозвуковой скоростями. Первый — детона­ционный. Второй режим рас­пространения волны химической реакции происходит со скоростями, значи­тельно меньшими звуковых, и связан с молекулярными процессами теплопроводности и диффузии — это режим распространения пламени. При теп­ловом механизме распространения пламени тепло, выделившееся при хими­ческой реакции, теплопроводностью передается в соседние участки нереагировавшего газа, нагревает их и инициирует активную химическую реакцию. При цепном механизме распространение очага реакции происходит путем диффузии активных центров. Возможно, также и наиболее вероятно в реаль­ных случаях горения совместное действие диффузии и теплопровод­ности.

Опытные данные и теоретическое рассмотрение свидетельствуют о том, что при распространении пламени реакция идет в каждый момент времени в сравнительно (по сравнению с размерами камер сгорания) тонком слое — зоне реакции. В непосредственной близости от зоны реакции, также в тонком слое, происходит разогрев несгоревшей смеси. Поэтому в первом приближе­нии распространение пламени можно представить себе так: имеются две об­ласти — несгоревшего газа и продуктов реакции, разделенные поверхностью горения, толщиной которой можно пренебрегать и рассматривать ее как гео­метрическую поверхность, движущуюся относительно газа с известной ско­ростью — нормальной скоростью распространения пламени.

Уже из общих соображений можно предвидеть, что химическая реакция внутри фронта пламени будет протекать неравномерно — из-за резкой за­висимости скорости реакции от температуры она будет, главным образом, сосредоточена в части фронта пламени, прилегающей к горячим продуктам сгорания. Там, где температура пониже,- реакция протекает со значительно меньшей скоростью и поэтому ее вообще, можно не учитывать, а рассматри­вать только молекулярный перенос тепла и вещества. Эти процессы в пламени доминируют в силу "большого перепада температуры и концентраций реаги­рующих веществ, они и определяют в основном структуру пламени.

22. Подобие распределений температуры и концентраций в пламени

Структура ламинарного пламени описывается системой уравнений теплопроводности и диффузии. Рассмотрим самый простой случай когда фронт пламени плоский, а хим реакция описывается одним стехиометрическим уравнением , так что скорости превращения по каждому веществу связаны соотношением W_i/ν_i=W’_j/ν_j=W. В сист. коорд, движуйся вместе с фронтом пламени ур-я имеют вид: 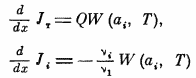(изменение теплового потока J_T и потоков реагирующих веществ J_i происходит вследствие тепловыделения и изменения кол-ва реагирующих в-в в хим. реакции). Здесь Q – теплота реакции, через a_i обозначены относительные весовые концентрации реагентов; скорость хим. Реакции рассчитана на моль в-ва, которому присвоен индекс 1. Будем считать, что это вещество в исходной смеси находится в недостатке. Потоки тепла и вещества скаладываются из конвективного и молекулярного переноса 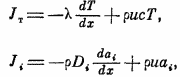, где D_i – коэф-ты диффузии, с- теплоемкость при постоянном давлении. 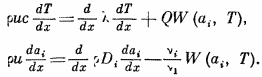С учетом уравнения неразрывности потомка массы в пламени pu=p₀u_n=p_bu_b=const, система ур-й может быть переписано в виде: Перейдем к рассмотрению газов близкого молекулярного веса. В этом случае коф-ты диффузии можно считать равными между собой. Кроме того, если потенциалы межмолекулярных сил между различными молекулами не сильно различаются, из кинетической теории газов следует, что коэ-ты диффузии приближенно равны коэф-ту температуропроводности газовой смеси во всем интервале температур D_i≈х В таких смесях несущественны также и перекрестные эффекты молекулярного тепломассопереноса (термодиффузия, диффузионная теплопроводность и др.). Утверждение о постоянстве суммы хим и тепловой энергии внутри пламени было высказано в 1934 г. Льисом и Эльбе в случае цепной реакции, инициируемой диффузией активных центров. Пусть скорость пламени определяется очень легкими активными центрами, концентрация которых очень мала; тогда ни диффузия, ни теплопроводность не успевают заметно изменить концентрационные и температурное поля. В этом случае реакция протекает, как в сосуде с подвижным поршнем (давление постоянно), и сохранение энтальпии очевидно. Такую ситуацию предст. себе эти ученые. Однако, постоянство полной энтальпии в стационарном потоке зависит не от механизма реакции, а от соотношения между коэф диффузии и теплопроводности смеси. Полные энтальпии исходной смеси и продуктов равных между собой при любых соотношениях между х и D – это закон сохранения энергии. Но, если выполнено еще условие x=D, а скорости превращения реагирующих веществ связаны стехиометрическими соотношениями (простая реакция), то полная энтальпия постоянна и внутри пламени. При постоянной теплоемкости постоянство полной энтальпии внутри пламени может быть записано в виде: Qa+cT=Qa₀+cT₀=cT_b, т.е. распределения температуры и концентрации оказываются подобными (a₀-a)/a₀=(T-T₀)/(T_b-T₀). Точно так же подобны между собой распределения температуры и распределения концентраций остальных реагирующих веществ, а также концентраций продуктов сгорания, если, конечно, их коэффициенты диффузии тоже равны х. Подобие имеет место и в тех случаях, когда скорость простой реакции зависит от концетраций конечных продуктов реакции (обратимая реакция или автокатализ конечными продуктом). Если реакция является сложной, то концентрации промежуточных продуктов не связаны стехиометрическими соотношениями, и подобия полей нет. Но и в этом случае при равенстве всех коэф переноса (D_i=x) полная энтальпия системы также остается постоянной – Н=const, однако отсюда нельзя получить однозначную зависимость a_i=f(T) для каждого из веществ, участвующих в реакции.