
Алгоритм с4.5
Представляє собою покращений варіант алгоритма ID3. Серед покращень потрібно відмітити наступні:
можливість працювати не тільки з категоріальними атрибутами, але й з числовими. Для цього алгоритм розбиває область значень незалежної змінної на декілька інтервалів і ділить початкову множину на підмножини відповідно з тим інтервалом, в який попадає значення залежної змінної;
після побудови дерева відбувається обрізання його віток. Якщо отримане дерево занадто велике, то виконується або групування декількох вузлів в один лист, або заміщення вузла дерева нижчерозміщеним піддеревом. Перед операцією над деревом обчислюється помилка правила класифікації, який міститься в поточному вузлі. Якщо після заміщення (або групування) помилка не збільшиться (і не сильно збільшиться ентропія), це означає, що заміну можна виконати без втрат для побудованої моделі.
Один з недоліків алгоритму ID3 є те, що він некоректно працює з атрибутами, які мають унікальні значення для всіх об'єктів з вибірки. Для таких об'єктів інформаційна ентропія дорівнює нулю і ніяких нових даних від залежної змінної отримати не вдасться. Оскільки після розбиття отримувані підмножини будуть містити по одному об'єкту.
Алгоритм C4.5 вирішує цю проблему шляхом введення нормалізації. Оцінюється не кількість об'єктів того чи іншого класу після розбиття, а число підмножин і їх потужність (число елементів).
Вираз

оцінює потенційну інформацію, що отримується при розбитті множини Т на m підмножин.
Критерієм вибору змінної для розбиття буде вираз:

або

За
умови, що є k класів і n (число об'єктів в
навчальній вибірці і кількість значень
змінних), тоді чисельник максимально
буде рівний ,
а знаменник максимально рівний
,
а знаменник максимально рівний
 . Якщо
припустити, що кількість об'єктів значно
більше кількості класів, то знаменник
зростає швидше, ніж чисельник і,
відповідно, значення виразу буде
невеликим.
. Якщо
припустити, що кількість об'єктів значно
більше кількості класів, то знаменник
зростає швидше, ніж чисельник і,
відповідно, значення виразу буде
невеликим.
У вибірці можуть бути об'єкти з пропущеними значеннями атрибутів. У цьому випадку їх або відкидають (що дає ризик втратити частину даних), або застосувати підхід, який припускає, що пропущені значення розподілені пропорційно частоті появи існуючих значень.
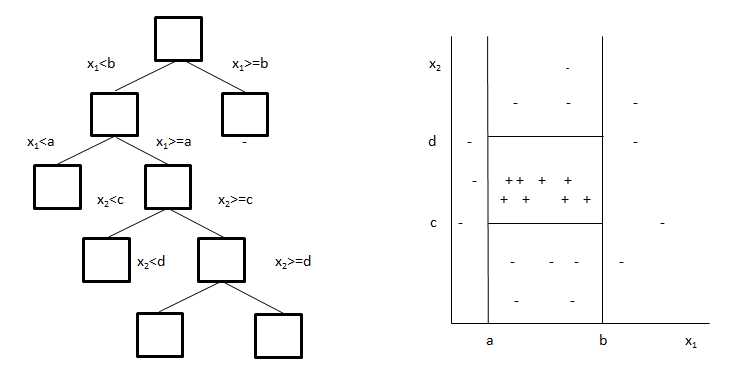
Ідею алгоритму можна представити у графічному вигляді (рис 5.4). При наявності в об’єктів тільки двох змінних, то їх можна представити у вигляді точок двовимірного простору. Об’єкти різних класів відмічені знаками «+»і«-». З рисунку видно, що при розбитті множини на підмножини будується дерево, що покриває тільки об’єкти вибраного класу.
Для постановки правил з використанням даного алгоритму необхідно щоб у навчальній вибірці були присутні все можливі комбінації значень незалежних змінних. Наприклад, дані, що дозволяють порекомендувати тип контактних лінз, представлені у табл. 5.2
Вік |
Приписання |
Астигматизм |
Ступінь зносу |
Рекомендації |
Юний |
Короткозорість |
Ні |
Понижений |
Ні |
Юний |
Короткозорість |
Ні |
Нормальний |
М’які |
Юний |
Короткозорість |
Так |
Понижений |
Ні |
Юний |
Короткозорість |
Так |
Нормальний |
Жорсткі |
Юний |
Далекозорість |
Ні |
Понижений |
Ні |
Юний |
Далекозорість |
Ні |
Нормальний |
М’які |
Юний |
Далекозорість |
Так |
Понижений |
Ні |
Юний |
Далекозорість |
Так |
Нормальний |
Жорсткі |
Літній |
Короткозорість |
Ні |
Понижений |
Ні |
Літній |
Короткозорість |
Ні |
Нормальний |
М’які |
Літній |
Короткозорість |
Так |
Понижений |
Ні |
Літній |
Короткозорість |
Так |
Нормальний |
Жорсткі |
Літній |
Далекозорість |
Ні |
Понижений |
Ні |
Літній |
Далекозорість |
Ні |
Нормальний |
М’які |
Літній |
Далекозорість |
Так |
Понижений |
Ні |
Літній |
Далекозорість |
Так |
Нормальний |
Ні |
Старечий |
Короткозорість |
Ні |
Понижений |
Ні |
Старечий |
Короткозорість |
Ні |
Нормальний |
Ні |
Старечий |
Короткозорість |
Так |
Понижений |
Ні |
Старечий |
Короткозорість |
Так |
Нормальний |
Жорсткі |
Старечий |
Далекозорість |
Ні |
Понижений |
Ні |
Старечий |
Далекозорість |
Ні |
Нормальний |
М’які |
Старечий |
Далекозорість |
Так |
Понижений |
Ні |
Старечий |
Далекозорість |
Так |
Нормальний |
Ні |
На кожному кроці алгоритму вибирається значення змінної, що розділяє всю множину на дві підмножини так, щоб всі об’єкти класу, для якого будується дерево, належали одній підмножині. Таке розбиття проводиться до тих пір, поки не буде побудована підмножина, зо містить тільки об’єкти одного класу.
Для вибору незалежної змінної і її значення, яке розділяє множину, виконуються наступні дії:
З побудованої на попередньому етапі підмножини (для першого етапу це вся навчальна вибірка), що включає об’єкти, що відносяться до вибраного класу для кожної незалежної змінної, вибираються всі значення, що зустрічаються в даній підмножині.
Для кожного значення кожної змінної підраховується кількість об’єктів, що задовольняють дану умову і відносяться до вибраного класу.
Вибираються умови, що покривають найбільшу кількість об’єктів вибраного класу.
Вибрана умова є умовою розбиття підмножини на дві нових.
Після побудови дерева для одного класу аналогічні дії виконуються для інших класів.
Приведемо приклад для даних, представлених у табл. 5.2. Нехай потрібно побудувати правило для визначення умов, при яких необхідно рекомендувати жорсткі лінзи:
якщо (?) рекомендація = жорсткі
Виконуємо оцінку кожної незалежної змінної і всіх її можливих значень:
вік = юний – 2/8;
вік = літній – 1/8;
вік = старечий – 1/8;
приписання = короткозорість – 3/12;
приписання = далекозорість – 1/12;
астигматизм = ні – 0/12;
астигматизм = так – 4/12;
ступінь зносу = низька – 0/12;
ступінь зносу = нормальна 4/12.
Вибираємо змінну і значення з максимальною оцінкою астигматизм = так. Таким чином отримуємо уточнене правило наступного виду:
якщо (астигматизм = так і ?) тоді рекомендація = жорсткі.
Дане правило утворює підмножину, в яку входять об’єкти, що відносяться до класу жорсткі. Крім них до неї входять і інші об’єкти, відповідно правило необхідно уточняти (табл. 5.4).
Вік |
Приписання |
Астигматизм |
Ступінь зносу |
Рекомендації |
Юний |
Короткозорість |
Так |
Понижений |
Ні |
Юний |
Короткозорість |
Так |
Нормальний |
Жорсткі |
Юний |
Далекозорість |
Так |
Понижений |
Ні |
Юний |
Далекозорість |
Так |
Нормальний |
Жорсткі |
Літній |
Короткозорість |
Так |
Понижений |
Ні |
Літній |
Короткозорість |
Так |
Нормальний |
Жорсткі |
Літній |
Далекозорість |
Так |
Понижений |
Ні |
Літній |
Далекозорість |
Так |
Нормальний |
Ні |
Старечий |
Короткозорість |
Так |
Понижений |
Ні |
Старечий |
Короткозорість |
Так |
Нормальний |
Жорсткі |
Старечий |
Далекозорість |
Так |
Понижений |
Ні |
Старечий |
Далекозорість |
Так |
Нормальний |
Ні |
Виконуємо повторну оцінку для незалежних змінних, що залишились, і їх значень, але вже на новій множині:
вік = юний – 2/4;
вік = літній – 1/4;
вік = старечий – 1/4;
приписання = короткозорість – 3/6;
приписання = далекозорість – 1/6;
ступінь зносу = низька – 0/6;
ступінь зносу = нормальна – 4/6.
Після уточнення отримаємо правило і множину, представлену в табл. 5.5:
якщо (астигматизм = так і ступінь зносу = нормальна) то рекомендація = жорсткі.
Вік |
Приписання |
Астигматизм |
Ступінь зносу |
Рекомендації |
Юний |
Короткозорість |
Так |
Нормальний |
Жорсткі |
Юний |
Далекозорість |
Так |
Нормальний |
Жорсткі |
Літній |
Короткозорість |
Так |
Нормальний |
Жорсткі |
Літній |
Далекозорість |
Так |
Нормальний |
Ні |
Старечий |
Короткозорість |
Так |
Нормальний |
Жорсткі |
Старечий |
Далекозорість |
Так |
Нормальний |
Ні |
Так як у отриманій множині залишаються об’єкти, що не належать класу жорсткі , то необхідно виконати уточнення:
вік = юний – 2/2;
вік = літній – 1/2;
вік = старечий – 1/2;
приписання = короткозорість – 3/3;
приписання = далекозорість – 1/3;
Очевидно, що уточнене правило матиме наступний вигляд:
якщо (астигматизм = так і ступінь зносу = нормальна і приписання = короткозорість) то рекомендація = жорсткі.
Однак в отриманій підмножині відсутній один з об’єктів, що відноситься до класу жорсткі, тому необхідно вирішити, яке з двох останніх правил більш прийнятне для аналітика.
Переваги використання дерев рішень:
швидкий процес навчання;
створення правил в областях, де експерту важко формалізувати свої знання;
інтуїтивно зрозуміла класифікаційна модель;
висока точність прогнозу, порівнянна з іншими методами (статистика, нейронні мережі);
Області застосування дерев рішень.
Дерева рішень є прекрасним інструментом в системах підтримки прийняття рішень, інтелектуального аналізу даних (data mining). До складу багатьох пакетів, призначених для інтелектуального аналізу даних, уже включені методи побудови дерев рішень.
Дерева рішень успішно застосовуються для вирішення практичних завдань у наступних областях:
банківська справа, - оцінка кредитоспроможності клієнтів банку при видачі кредитів.
промисловість, - контроль за якістю продукції (виявлення дефектів), випробування без руйнувань (наприклад перевірка якості зварювання) і т.д.
медицина, - діагностика захворювань.
молекулярна біологія, - аналіз будови амінокислот.
