Новый раздел

Особенности применения IRR

1. IRR – относительный показатель, его отличие от NRV, в том, что NRV – абсолютный показатель.

Основной недостаток NRV в том, что он не может дать информацию о так называемом «резерве безопасности», т.е. если в прогнозе денежного потока или коэффициента дисконтирования была допущена ошибка, то NRV не покажет того порогового значения, где проект убыточен.

Информацию о резерве безопасности дают критерии IRR и PI. Разница IRR и WACC дает запас безопасности. Чем он больше, тем ниже вероятность того, что риск ошибки прогноза сделает проект убыточным.

По критерию PI: чем больше значение PI превосходит единицу, тем больше резерв безопасности.

Таким образом, с позиции риска можно сравнивать два проекта по критериям IRR и PI, но нельзя по критерию NRV.

2. Зависимость NRV от ставки дисконтирования нелинейная, степень этой зависимости различная и определяется динамикой денежного потока.

Пример.

Проекты А и В являются независимыми. Требуется проран­жировать их по степени приоритетности, при условии, что цена потока финансирования неопределенна и варьирует от 5 до 20 процентов.

	Значение, млн. руб
Убывающие потоки А	-200	150	80	15	15	10
Нарастающие потоки В	-200	20	50	50	90	110

проект	Значение NRV при r				IRR, %
	r=5%	r=10%	r=15%	r=20%
А	48,6	30,2	14,3	0,5	20,2
В	76,5	34,3	0,7	-26,5	16,0

При переходе от 10% до 15%.

NRV снижается в проекте А на -52.6 %:

14.3 / 30.2*100 %-100 %= -52.649 %.

В проекте В на –98.0%:

0.7 / 34.3*100 %-100 % = -97.959 %.

Это связано с тем, что в проекте А потоки убывающие и поэтому, они более интенсивно возмещаются в начале жизненного цикла и в меньшей степени реагируют на увеличение ставки дисконтирования.

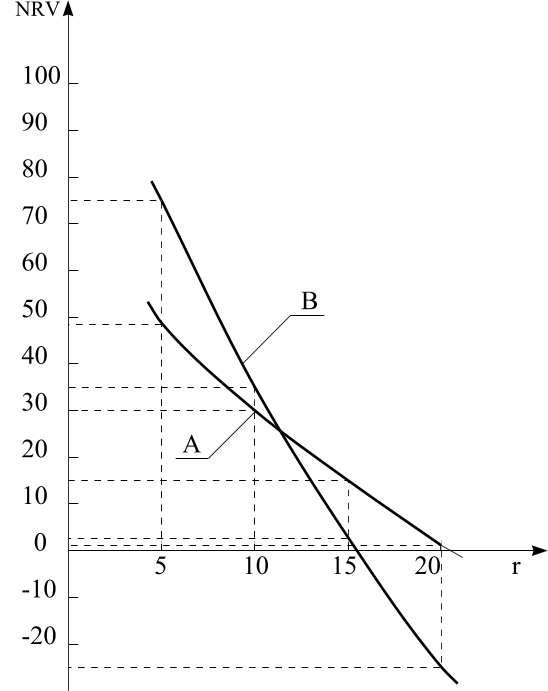
Рисунок.

3. В классических инвестиционных проектах IRR показывает лишь максимально допустимый уровень расходов, который может быть ассоциирован с этим проектом. При оценке альтернативных инвестиционных проектов, даже при IRR>WACC, выбор может быть сделан лишь с помощью дополнительных критериев.

Пример.

Проекты А и В являются альтернативными. Требуется выбрать один из них при условии, что цена капитала, предназначенного для инвестирования составляет а) 8%; б) 15%.

Проект	Величина инвестиций	Денежный поток по годам, млн. руб.			IRR, %	точка Фишера
		1	2	3		r, %	NRV
A	-100	90	45	9	30	10	26
B	-100	10	50	100	20.4	10	26
B-A	0	-80	5	91	10	-	-

.

При WACC=8 % и при WACC=15% оба проекта Аи В приемлемы, поскольку в обоих случаях IRR>WACC. Для выбора инвестиционного проекта построим графики NRV.(см. рисунок).

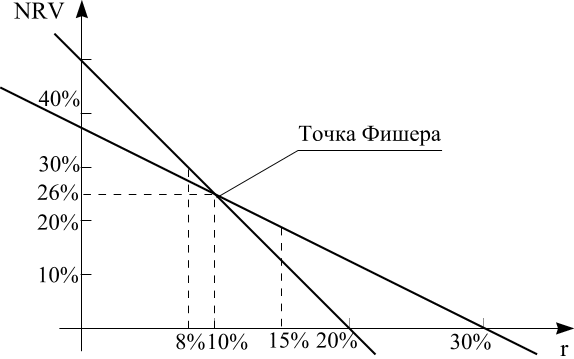
Рисунок.

Точка Фишера показывает значение коэффициента дисконтирования, при котором оба проекта имеют одинаковый NRV.

Точка Фишера является пограничной точкой, разделяющей ситуации, ко­торые улавливаются NRV и не улавливаются критерием IRR.

В данном случае IRR не может расставить приоритеты между проектами, также он не показывает различия между ситуациями а) и б).

Критерий NRV позволяет расставить приоритеты в любой ситуации и показывает, что а) и б) принципиально различаются между собой.

Если WACC=8%, то следует предпочесть проект А, так как он дает больший NRV. Если WACC=15%, то следует выбрать проект В ( NRV(B)>NRV(A) ).

WACC=8%. NRV(A)>NRV(B)  принять проект А.

WACC=15%. NRV(A)<NRV(B)  принять проект B.

Точку Фишера можно найти как IRR приростного потока (А-В) или, что то же самое (В-А).

Оценка сложных инвестиционных проектов

В сложном инвестиционном проекте оттоки и притоки денежных средств чередуются. Это связано с необходимостью демонтажа оборудования, затратами на восстановление окружающей среды и др. В этом случае IRR может меняться, и следовательно, выводы, сделанные на основе IRR не всегда корректны.

IRR=r, при котором

Уравнение может иметь столько решений, сколько раз меняется знак денежного потока, следовательно возможно существования несколькоих значений IRR

Ловушка 1:множественность значений IRR.

Проект	Величина инвестиций	Основной поток по годам, млн. руб.			IRR, %
		1	2	3
А	-1000	6000	-11000	6000	0 100 200

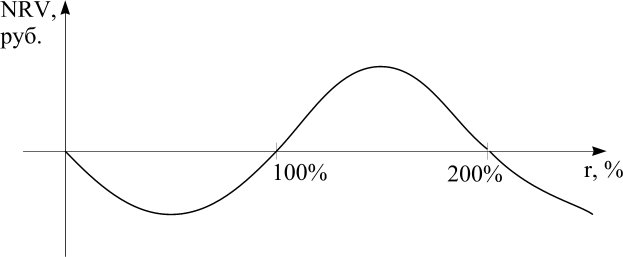
Рисунок. NRV проекта А.

Ловушка 2: взаимоисключающие проекты.

Большая IRR проекта не всегда соответствует большей величине NRV. Без рассмотрения эффективности приростных капитальных вложений IRR не может служить надежным критерием для ранжирования инвестиционных проектов различных масштабов.

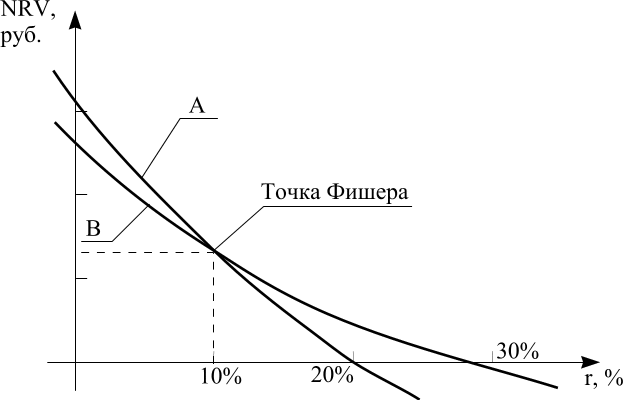
Рисунок

Заключение.

В прямых проектах чем выше IRR, тем выше оценка, в обратных - наоборот, худшие проекты имеют более высокое значение IRR. В сложных проектах возможно несколько корней, поэтому принятие решения невозможно без графика NRV. Следовательно, NRV явно предпочтительнее IRR при оценке сложных инвестиционных проектов.