Задача о наборе высоты и скорости самолетов.

Постановка. Самолет находится на высоте и имеет некоторую скорость . Требуется найти минимальные затраты топлива, которые позволили бы ему подняться на высоту и приобрести скорость . Для ее решения также применим метод динамического программирования. При инвариантном погружении вводится декартова система координат на плоскости. При инвариантном погружении отрезки [ , ] и [ , ] разбиваются на некоторое количество равных частей и делается предположение, что в результате отдельной операции самолет может набирать скорость, т.е. двигаться по оси , либо только набирать высоту.

Расходы на отдельную операцию считаются известными. Задача решается по той же схеме, что и нахождение более экономичного пути.

2.1.Марковские процессы. Постановка. Граф состояний для конечной цепи.

Постановка: Пусть имеется некоторая система состояния, которой известны и изменяются во времени под действием некоторых случайных процессов. Предположим, что известны вероятности перехода системы из данного состояния во все остальные. Требуется ответить на вопросы: в каком состоянии система пребывает наиболее часто; с какой вероятностью система может находиться в том или ином состоянии в некоторый момент времени.

Процесс изменения состояния объекта называется марковским, если его поведение в будущем зависит лишь в каком состоянии он находится в данный момент и не зависит от предыстории. Состояние объекта описывает набор некоторых параметров, которые называются фазовыми координатами, а процесс изменения состояния представляет из себя некоторую фазовую кривую из некоторого фазового пространства. Если количество состояний в марковском процессе счетно, то такой процесс называется марковской цепью. Вероятность перехода в практическое состояние в некоторый момент времени зависит лишь от того, в каком состоянии находится система в данный момент и как система пришла в это состояние.

Марковская цепь называется стационарной, если различные моменты времени .

В этом случае марковская цепь характеризуется матрицей перехода

, , .

Марковская цепь может характеризоваться и графиком состояний, узлами которой служат возможные состояния системы, а дуги вместе с числовыми показателями характеризуют переход из одного состояния времени некоторую вероятность.

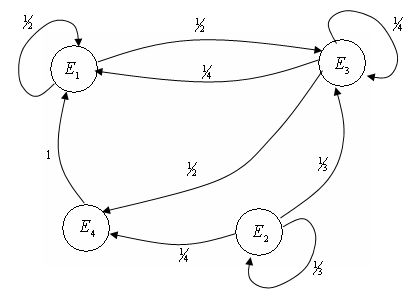
Матрица переходов имеет вид

Переход системы из одного состояние в другое осуществляется в некоторые дискретные моменты времени

2.2-2.3. Вычисление некоторых характеристик марковских цепей. Примеры. Потоки событий. Пуассоновский поток.

.

- вероятность, с которой в m-ый момент переключения цепь находится в состоянии . Нам требуется выяснить эти вероятности, при этом предполагается, что известны - вектор определяющий начальное состояние цепи.

Очевидно, что выполняются условия:

…

2

. (1)

По предыдущей формуле мы можем рассчитать вектор для любого через и .

Опр. Марковская цепь наз. эргодической, если ее любое состояние , может быть достигнута из состояния за конечное число переключений с ненулевой вероятностью.

Для эргодической цепи существует , и числа называются предельными вероятностями нахождения цепи в состоянии .Они характеризуют среднюю долю время на достаточно большом временном промежутке нахождения системы в этом состоянии.

Например, если и рассматриваемый временной промежуток T={1 год}, то это означает, что система находится в сост. 4 месяца. С помощью предельных вероятностей затем легко находятся производные характеристики для марковских цепей. Чтобы подсчитать достаточно перейти к пределу в формуле (2). , .

.

- однородная система из n уравнений, с n неизвестными. Из свойств вероятности детерминант этой системы равен 0, т.е. она имеет бесконечное множество решений, а чтобы найти одно решение нужно (3).

Из системы (3) можно вычислить предельные вероятности.