Смешанные стратегии. Основная теорема матричных игр.

Определение. Вектор , , называется смешанной стратегией первого игрока, где означает вероятность (при бесконечном количестве розыгрышей), либо частоту, с которой он выбирал свои ходы .

Определение. Вектор , , называется смешанной стратегией второго игрока, где означает вероятность либо частоту, с которой второй игрок выбирает свой ход .

Определение. Пусть – множество смешанных стратегий первого игрока, – множество смешанных стратегий второго игрока. Если зафиксировать и в ней окажется больше нулей, то ход будем называть активным, а если , то ход называется пассивным.

Определение. Если зафиксировать и в ней , то ход активен, а если , то пассивен.

Определение. Пусть в процессе розыгрышей первый игрок все время выбирает ход , тогда можно говорить, что он выбирает смешанную стратегию , где 1 стоит на i-ом месте. Такая стратегия называется чистой.

Аналогично для второго игрока.

Пусть первый игрок выбирает некоторую смешанную стратегию , а второй - . Тогда его средний выигрыш (мат. ожидание) вычисляется по формуле - это будет средний выигрыш для первого и проигрыш для второго.

Теорема (основная теорема теории игр). В любой матричной игре существует – оптимальная смешанная стратегия первого игрока и – оптимальная смешанная стратегия второго игрока такие, что , , . При этом называется ценой игры.

Решение игры 2×2, 2×n и m×2

Теорема: Пусть 1 игрок выбирает - оптим. смешанную стратегию, тогда его средний выигрыш все равно будет , если 2 игрок выбирает любую смешанную стратегию, не выходящую за пределы активных ходов из . Аналог. утв. справедливо для 2 игрока. Пусть 1 игрок придерживается своей стратегии , тогда

Пусть 2 игрок придерживается . Тогда Для реш. матричной игры достаточно сост. 2 системы и их решить.

Общая схема решения игры .

1. вводим систему координат и проводим линию

2. для каждого хода строим соответствующий отрезок, j=

3. строим нижнюю ломаную из кусков

4. находим верхнюю точку этой нижней ломаной и определяем какие ходы второго игрока будут активными в игре (пересекаются в этой точке)

5. строим эквивалентную игру и две алгебраические системы для нахождения оптимальных стратегии ( для пассивных ходов).

Схема решения игры .

1. строим систему координат и проводим линию

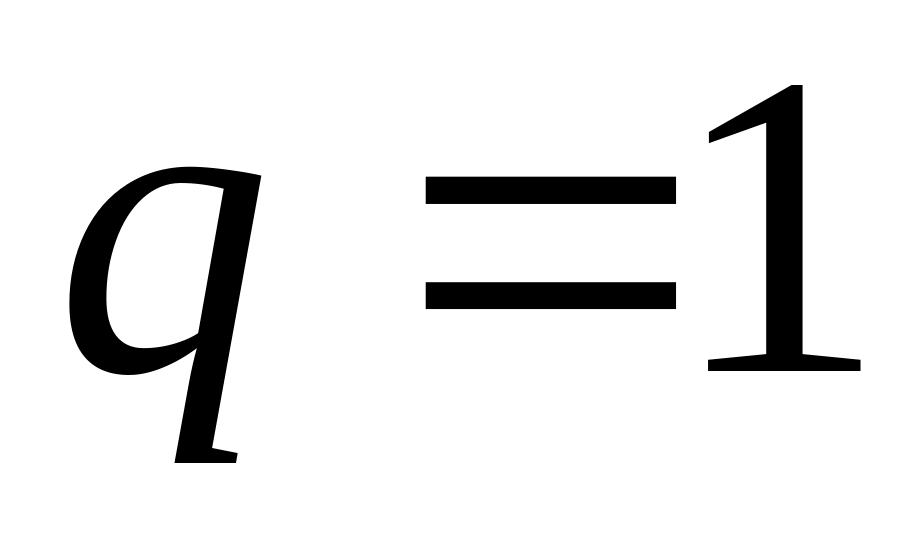
2. для каждого хода строим соответствующий отрезок, i=

3. находим верхнюю ломаную из этих отрезков

4. определяем нижнюю точку этой ломаной и определяем какие ходы первого игрока будут пересекаться в ней, т.е. являться активными

5. составляем пару алгебраических систем и определяем оптимальные смешанные стратегии игроков и .

Решение игры m x n.

П усть 1 игрок придерживается смешанной стратегии .

Если 2 игрок выбирает свой чистый ход , то выигрыш 1 игрока будет

, тогда . Делим все нер-ва системы на полож. число и введем обозначение , .

(4)

для любого (3)

(*)

Так как 1 игрок стремиться выиграть как можно больше, т.е. , тогда для 2 игрока

(5)

(6)

Приходим к задаче ЛП (5), (4), (6). Нетрудно убедиться, что у этой задаче существует О.П.

Подставив его в (*) найдем – цена игры, а совершив затем в (3) обратное преобразование, получим

, – оптим. смеш. стратегия 1 игрока.

Так, решение игры для первого игрока свелось к решению задачи ЛП.