5) При задании матрицы
А =(1 2 3
4 5 6)
ее можно рассматривать как
вектор-столбец из двух элементов, каждый из которых является вектор-строкой из трех элементов, поэтому необходимо использовать запятые или пробелы для разделения элементов в одной строке и точку с запятой в качестве разделителя строк.
» А = [1 2 3; 4 5 6] ;
Еще один способ ввода матрицы состоит в том, что матрицу можно рассматривать как векгор-строку, каждый элемент которой является вектор-столбцом.
Например, матрицу А можно ввести при помощи команды » А = [[1; 4] [2; 5] [3; 6] ] ;
Как и в случае одномерных массивов, двумерный массив можно создать, прописывая все его элементы:
» А<1,1) = 1; А<1,2) = 2; А<1,3) = 3; » А<2,1) = 4; А<2,2> = 4; А<2,3) = 6;
Конструкторы вида [А В; CD], где А, В, С, D –элементы, которые сами могут быть матрицами, создают матрицу (A B
C D)
При этом должна соблюдаться согласованность по количеству строк матриц А и В, С и D соответственно, а также по количеству столбцов матриц А и С, В и D.
Для задания ряда матриц специального вида имеются команды MATLAB, аргументами которых являются размерности создаваемых матриц (см. табл. 2.4). Если указано одно число N, то формируется квадратная матрица NxN.
11мм |
Назначение |
diag |
Создание диагональной матрицы или выделение диагонали |
eye |
Единичная матрица |
gallery |
Функция, позволяющая получать более пятидесяти стандартных матриц |
hilb |
Гильбертова матрица |
magic |
Матрица магического квадрата |
ones |
Матрица из единиц |
rand |
Случайная матрица со значениями из интервала [0,1] |
randn |
Создание матриц равномерно распределенных случайных чисел |
tril |
Выделение нижней части треугольной матрицы |
triu |
Выделение верхней части треугольной матрицы |
zeros |
Нулевая матрица |
6) операция формирования диапазона значений, обозначаемая двоеточием. Например составим одномерный массив diap1, состоящий из всех вещественных чисел от 3.7 (включительно) с приращением 0.3 и не более 8.947. Для этого применяем операцию, обозначаемую двоеточием:
diap1 = 3.7 : 0.3 : 8.947 ;
7.Конкатенацией называют объединение массивов, которое реализует следующая функция.С = cat (dim, А, В) — объединяет массивы А и В в соответствии со спецификацией размерности dim и возвращает объединенный массив; dim = 1 — горизонтальная конкатенация, dim = 2 — вертикальная, dim = 3 — многомерный массив размерности 3 и т. д.; С = cat(dim,Al,A2,A3,A4,...) объединяет все входные массивы (А1, А2, A3, А4 и т. д.) в соответствии со спецификацией размерности dim и возвращает объединенный массив;cat(2.A,B) — это то же самое, что и [А,В],асаt(,А,В) —то же самое, что и [А; В]. При записи cat (dim, С (:)) или cat (dim, С. field) эта функция применима к массивам ячеек или структур, содержащим численные матрицы. Пример:
» A =[2.4:3,5];B=[8,7;9.0];C=cat(1.A.B)
С =
2 4
3 5
8 7
9 0
Разделителем элементов формируемого одномерного массива может быть либо пробел, либо запятая. При использовании выражений и комплексных чисел использование запятой предпочтительнее.
8.Разделителем строк в формируемом с помощью операции конкатенации двумерном массиве служит точка с запятой. С = cat (dim, А, В) — объединяет массивы А и В в соответствии со спецификацией размерности dim и возвращает объединенный массив; dim = 1 — горизонтальная конкатенация, dim = 2 — вертикальная, dim = 3 — многомерный массив размерности 3 и т. д.; С = cat(dim,Al,A2,A3,A4,...) объединяет все входные массивы (А1, А2, A3, А4 и т. д.) в соответствии со спецификацией размерности dim и возвращает объединенный массив;cat(2.A,B) — это то же самое, что и [А,В],асаt(,А,В) —то же самое, что и [А; В]. При записи cat (dim, С (:)) или cat (dim, С. field) эта функция применима к массивам ячеек или структур, содержащим численные матрицы. Пример:
» A =[2.4:3,5];B=[8,7;9.0];C=cat(1.A.B)
С =
2 4
3 5
8 7
9 0
9. Многомерныe массив - это расширение понятия числового массива, когда количество измерений (размерность) становится больше двух. Многомерные массивы применяются при описании страниц двумерных данных.
MATLAB поддерживает следующие функции при работе с многомерными массивами:
Функция |
Назначение |
cat |
Сформировать многомерный массив. |
ndims |
Определить размерность многомерного массива. |
ndgrid |
Сгенерировать сетку для многомерной функции. |
permute, ipermute |
Переставить размерности. |
shiftdim |
Изменить размерность массива. |
squeeze |
Удалить одну из размерностей. |
Пользователь может расширить состав этих функций, создавая специальные М-файлы для обработки конкретных данных. Для создания многомерных массивов можно использовать те же приемы индексирования и применения встроенных функций, которые используются при создании двумерных массивов. Тем не менее в системе MATLAB добавлена специальная функция cat, которая позволяет сформировать структуру многомерного массива. Таким образом, можно определить три подхода к созданию многомерных массивов:
использование индексов;
использование встроенных функций для формирования массивов специального вида;
использование функции cat.
Использование индексов. Один из способов формирования многомерного массива вытекает из его представления как совокупности 2-мерных массивов, размещаемых на новых страницах. Он состоит в том, чтобы просто добавлять новые размерности для формирования нужных страниц (3-ю, 4-ю, 5-ю и т. д.). ПРИМЕР A(:, :, 3) = 5
|
|
|
|
|
|
|
|
|
Рис. 5.4. 3-мерный массив размера 3х3х3.
Дополним массив А четвертой размерностью, введя
A(:, :, 1, 2) = [1 2 3; 4 5 6; 7 8 9]; A(:, :, 2, 2) = [9 8 7; 6 5 4; 3 2 1]; A(:, :, 3, 2) = [1 0 1; 1 1 0; 0 1 1]
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5.5. 4-мерный массив размера 3х3х3х2.
Использование встроенных функций. Такие встроенные функции системы MATLAB, как randn, ones и zeros, могут быть использованы для формирования многомерных массивов, поскольку каждый аргумент такой функции определяет размер соответствующего измерения
11. РАЗМЕРНОСТЬ МАССИВА (dimension). Количество индексов, необходимое для однозначной идентификации любого элемента массива. Массив, элемент которого - переменная с одним индексом, называется одномерным массивом, с двумя индексами - двумерным и т. д. Для вычисления размера каждой размерности массива используется функция size:М = size(A.DIM) возвращает размер размерности, указанной скаляром DIM, в виде вектора-строки размером 2. Для двумерного или одномерного массива А size(A.l) возвращает число рядов, a size (А, 2) - число столбцов;Для N-мерных массивов А при n>2 size(A) возвращает N-мерный вектор-строку, отражающий страничную организацию массива, последняя составляющая этого вектора равна N. В векторе отсутствуют данные о единичных размерностях (тех, где расположены вектор-строка или вектор-столбец, т. е. size(A,DIM)==l). Исключение представляют N-мерные массивы Java массивов javaarray, которые возвращают размер массива самого высокого уровня.Вообще, когда входным аргументом size является javaarray, то возвращаемое число столбцов всегда 1, а число рядов (строк) равно размеру (длине) javarray.
[Ml, М2 ,МЗ,..., MN] = si ze(A) возвращает размер первых N размерностей массива А;
D = size (А), для mxn матрицы А возвращает двухэлементный вектор-строку, в котором первая составляющая — число строк т, а вторая составляющая — число столбцов n;
[m.n] = size(A) возвращает число рядов и столбцов в разных выходных параметрах (выходных аргументах в терминологии MATLAB) тип.
12. Много приемов, связанных с работой с двумерными массивами, переносится на многомерные. В этом разделе описано, как применяется техника индексации и переопределения размеров к многомерным массивам.
В качестве сквозного примера будем рассматривать 3-мерный массив нормально распределенных случайных целых чисел nddata размера 4х5х3:
nddata = fix(8*randn(4, 5, 3)) nddata(:, :, 1) =
-3 |
-9 |
2 |
-4 |
8 |
-13 |
9 |
1 |
17 |
0 |
1 |
9 |
-1 |
-1 |
0 |
2 |
0 |
5 |
0 |
-6 |
nddata(:, :, 2) =
2 |
-5 |
-11 |
6 |
9 |
-10 |
6 |
4 |
5 |
-9 |
5 |
10 |
-3 |
10 |
0 |
12 |
-12 |
5 |
5 |
-1 |
nddata(:, :, 3) =
-12 |
-6 |
-17 |
4 |
3 |
2 |
4 |
0 |
13 |
-8 |
-8 |
1 |
-8 |
4 |
0 |
11 |
-7 |
4 |
-5 |
0 |
Индексация
Чтобы получить доступ к элементу (3, 2) на странице 2 массива nddata, надо использовать обращение nddata(3, 2, 2).
В качестве индексов можно использовать вектор, каждый элемент которого должен быть допустимым индексом многомерного массива. Чтобы получить доступ к трем элементам (2, 1), (2, 3) и (2, 4) на странице 3 массива nddata, надо использовать обращение
nddata(2, [1 3 4], 3) ans = 2 0 13
Индексация столбцов многомерных массивов. Индексация столбцов, широко применяемая в системе MATLAB, может быть распространена и на многомерные массивы.
Пример:
Чтобы получить доступ к столбцу 3 на странице 2 массива nddata, надо воспользоваться следующим оператором
nddata(:, 3, 2) ans =
-11 |
4 |
-3 |
5 |
Используя индексацию столбцов, можно извлечь следующий массив размера 2х2 со страницы 1 массива nddata:
nddata(2:3,2:3,1) ans =
9 |
1 |
9 |
-1 |
Индексация столбцов может быть использована как в правой, так и в левой частях оператора присваивания.
Пример.
Сформируем 2-мерный массив С размера 4х4, заполненный нулями:
C = zeros(4, 4) C =
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Теперь разместим в центре массива С подмассив nddata(2:3, 1:2, 2) размера 2х2, извлеченный из многомерного массива nddata:
C(2:3, 2:3) = nddata(2:3, 1:2, 2) C =
0 |
0 |
0 |
0 |
0 |
10 |
60 |
0 |
0 |
5 |
10 |
0 |
0 |
0 |
0 |
0 |
13. Следует помнить , что вектор, матрица или тензор являются математическими объектами, а одномерные, двумерные или многомерные массивы представляют способы хранения этих объектов в памяти компьютера.
14. матрицу можно рассматривать как вектор - столбец из двух элемен тов, каждый из которых является вектор - строкой из трех элементов, поэтому необходимо использовать запятые или пробелы для разделения элементов в одной строке и точку с запятой в качестве разделителя строк.
>> A = [1 2 3; 4 5 6];
Еще один способ ввода матрицы состоит в том, что матрицу можно рассматривать как вектор - строку, каждый элемент которой является вектоp- столбцом.
Например, матрицу A можно ввести при помощи команды
>> A = [[1; 4] [2; 5] [3; 6]];
Как и в случае одномерных массивов, двумерный массив можно создать, прописывая все его элементы:
>> A(1,1) = 1; A (1,2) = 2; A (1,3) = 3;
>> A (2,1) = 4; A(2,2) = 4; A (2,3) = 6;
Присваиванием значения последнему элементу:
>>B(2,3)=1
Создание матрицы операцией конкатенации матриц. Аналог функций cat(1,A1,A2), cat(2,A1,A2)
Блок-матрицы.
>> A1 = [1 2 3; 4 5 6]; A2 = (0 0 0; 1 1 1);
>> A =[A1 A2; A2, A1]
15. size(A):вектор с количеством строк и столбцов матрицы А.
size(A,k): k=1: количество строк, k=2:количество столбцов.
[r, c]=size(A): количество строк в r, количество столбцов в c.
length(A): возвращает max(size(A)) или 0 для пустой матрицы.
16. Для доступа к отдельным элементам матрицы используется выражение с круглыми скобками, в которых через запятую перечисляются его индексы.
- один индекс (порядковый номер элемента)
-группа индексов, разделяемых запятыми (первый индекс-номер строки, второй-номер столбца).
Первое значение индекса – 1, последнее значение – end.Отрицательное или нулевое значение индекса приводит к сообщению об ошибке.
В качестве индекса может задаваться вектор.
: - краткая форма записи 1:end.
Чтение несуществующего элемента: сообщение об ошибке
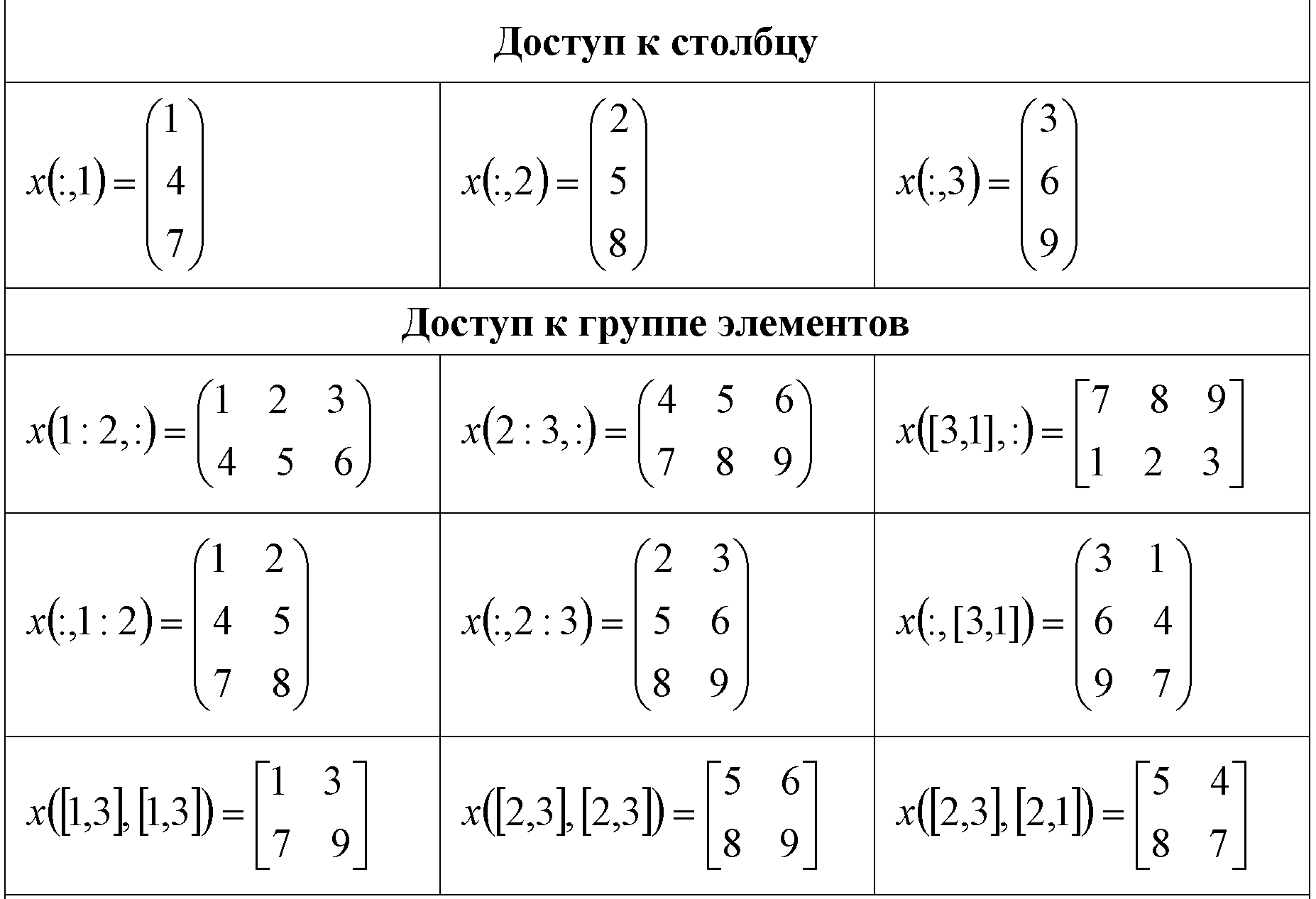
17.
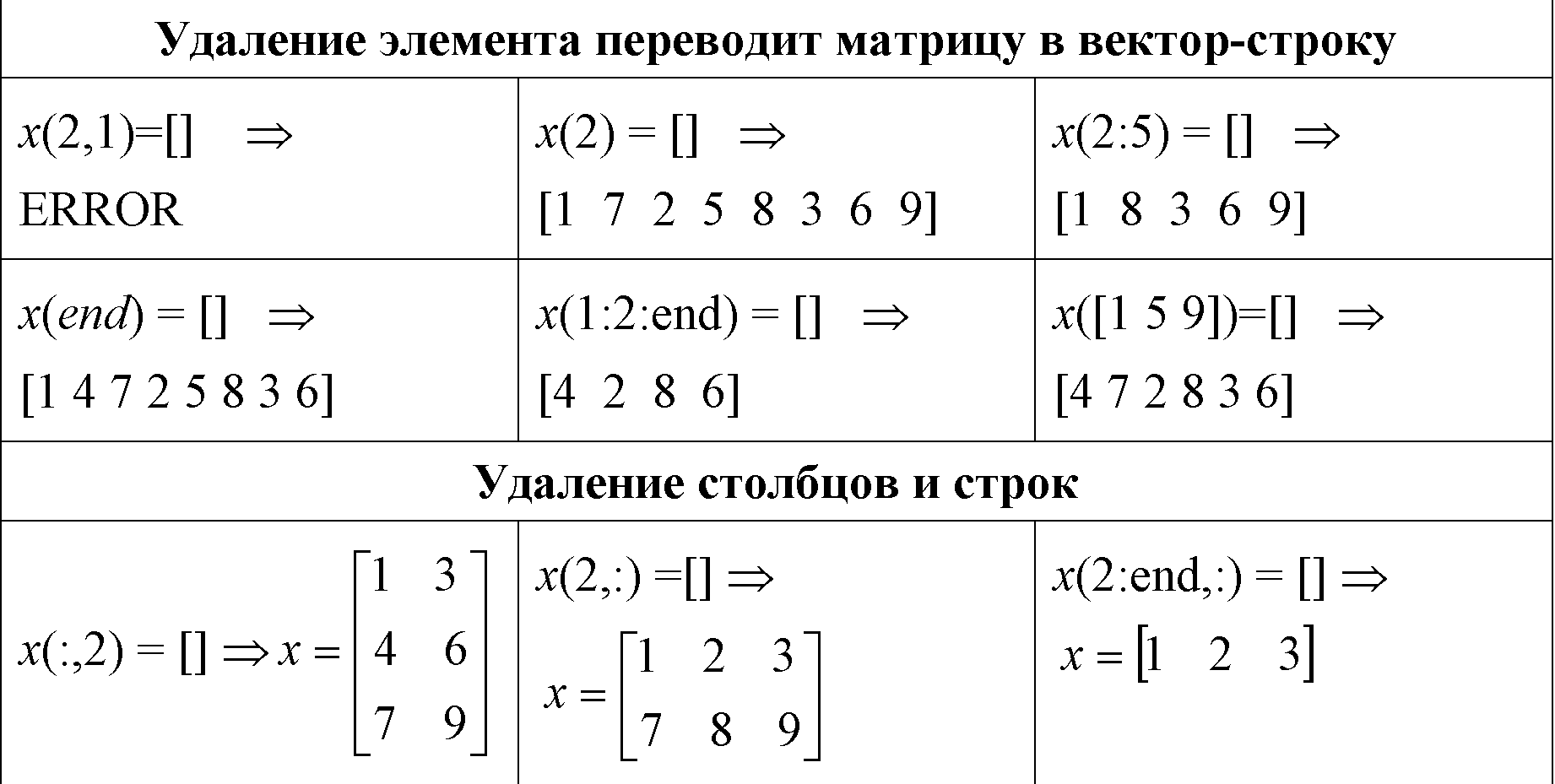
18. Система MATLAB позволяет переставлять строки (столбцы) массивов. Переставим местами столбцы в матрице x таким образом, чтобы последний столбец стал первым, второй – последним, а первый – вторым. Для этого следует выполнить операцию:
>> x = x(:,[3 1 2])
В результате
матрица примет вид
исходная матрица
19. min,max: максимальный (минимальный) элемент в каждом столбце/строке матрицы; двойное употребление приводит к нахожлению минимального(максимального) элемента во всей матрице
20. элементы которые имеют строковый тип (strings), так создаются структуктуры.
22..+, .-, .*, ./, .\, .^:поэлементные операторы сложения, вычитания, умножения, деления. Если один из операторов скаляр, то он воздействует на каждый элемент другого операнда;
А+В: матричное сложение, аналог А.+В;
А-В: матричное сложение, аналог А.-В;
А*В: матричное умножение(по правилу строка на столбец);
A^n: n-кратное матричное умножение;
X=A\B: правостороннее деление, решение системы линейных уравненийAX=B;
A.’: транспонирование матрицы;
A’: комплексно-сопряженное транспонирование матрицы.
При сложении, вычитании, умножении, делении матрицы на число соответствующая операция всегда производится поэлементно.
Аддитивные операции сложения и вычитания осуществляются с массивами по
элементно и обозначаются знаками. Складываемые (вычитаемые) матрицы должны иметь одинаковые размеры. Если операция применяется к матрицам, размеры которых не согласованы, то будет выведено сообщение об ошибке. В случае,если одно из слагаемых является скаляром , производится автоматическая генерация безымянной матрицы с таким же размером, как и у матричного слагаемого, при этом все ее элементы одинаковы и равны исходному скаляру.
Знак деления / (а также знак \ ) выполняет операцию нахождения решений систем линейных уравнений .
При поэлементном умно жении на скаляр производится расширение скаляра до матрицы , т. е. на скаляр умножается каждый элемент матрицы.
Для поэлементного деления используются комбинации знаков ./ и .\, обозначающие «правое» и «левое» поэлементные деления. Выражение A./B делит элементы первой матрицы на соответствующие элементы второй и приводит к матрице с элементами A(k,m)/B(k,m),а выражение A.\B служит для деления элементов второй матрицы на соответствующие элементы первой и приводит к матрице с элементами B(k,m)/A(k,m).
Обе матрицы должны иметь одинаковые размеры, в случае скаляра производится его расширение до размеров операнда-матрицы.
23. Логические выражения. Логические операторы, а также соответствующие им команды позволяют выполнять сравнения массивов одинакового размера. Применение логических операций к массивам приводит к поэлементному их выполнению над каждым элементом массива. Результатом является массив того же размера, что и исходный, состоящий из нулей и единиц. Одним из элементов логических операций может быть число. В этом случае происходит поэлементное выполнение логической операции для каждого элемента и числа. Выполнение бинарных логических операций xor, & и | над массивами разных размеров недопустимо.
Лог.ф-ии: &(and), |(or), ~(not), xor.
24. Как увидеть «портрет» матрицы. Функция spy рисует «портрет», или шаблон матрицы, в котором точками будут отмечены ненулевые элементы. После выполнения команды spy на экране появляется окно Figure№1. На вертикальной и горизонтальной осях откладываются номера строк и номера столбцов. Ненулевые элементы обозначаются маркерами. Внизу окна указывается число ненулевых элементов матрицы.
25. Способы создания текстовых строк. Для создания текстовых строк в системе MATLAB предусмотрен тип данных char («символ»). Текстовые данные, в том числе и одиночный символ, должны заключаться с обеих сторон в апострофы: >> s1 = 'a'; s2='abcd';
В результате таких присваиваний создаются переменные в виде массивов типа char. Печатаемые символы из стандартного набора ASCII во внутреннем представлении даны целыми числами от 32 до 255. Конвертировать массив символов в числовую матрицу позволяет команда double. Обратная операция выполняется по команде char.
По отношению к массивам символов справедливы также все операции, ранее рассмотренные для случая массивов типа double. Например, вместо группового присваивания s2='abcd' можно выполнить поэлементное присваивание с помощью операции индексации:
>> s2(1)='a'; s2(2)='b'; s2(3)='c'; s2(4)='d'
или осуществить операцию конкатенации
>>s2 = ['ab' 'c' 'd'].
26. Функции для работы с текстовыми строками. Текстовые строки используются для вывода в командное окно для информирования пользователя о ходе выполнения M-функции. Это осуществляется с помощью функции disp, принимающей в качестве аргумента текстовую строку
>> x= 17;
>> message= ['Variable x= ', int2str(x)];
>> disp(message)
А также для вывода сообщения, предупреждающего пользователя о необходимости ввода с клавиатуры значения переменной:
>> X = input('X = ? ')
Функция input выводит в командное окно текст, являющийся ее аргументом, после чего ожидает ввода значения с клавиатуры и нажатия клавиши <Enter>.
Для ввода текстового значения следует вызвать функцию input с двумя аргументами:
>> str=input('str= ', 's ')
В результате выполнения этой функции на экране появляется надпись,
после чего можно набирать необходимый текст с клавиатуры, заканчивая
ввод нажатием клавиши <Enter>. Если нажать <Enter>, не введя с клавиатуры никакого текста, то переменная str примет значение пустого массива. Перед использованием этой переменной следует проверить ее содержимое функцией isempty(str), возвращающей единицу, когда аргумент является пустым массивом.
Char(Перевод массива целых чисел в массив символов), num2str (Перевод числа в строку), int2str (Перевод целого числа в строку), mat2str (Преобразование матрицы в строку), str2mat (Объединение строк в матрицу), str2num (Перевод строки в число), str2double (Преобразование символьного вида числа в числовой), strcat (Объединение (сцепление) строк), strvcat (Вертикальное объединение (сцепление) строк ), findstr (Поиск подстроки в строке), strtok (Поиск первой подстроки, отделенной пробелами), strcmp (Сравнение строк), strcmpi (Сравнение строк без учета регистра), strncmp (Сравнение первых n символов двух строк), strrep (Замена в строке одной подстроки на другую), upper (Преобразование в прописные буквы), lower (Преобразование в строчные буквы), ischar (Проверка, является ли объект массивом символов), blanks (Вставка пробелов), deblank (Удаление пробелов в конце строки), strjust (Выравнивание элементов в строке), sprintf (Форматная запись в строку), sscanf (Чтение данных из строки в заданном формате)
27. Структуры, массивы структур. Структуры –объекты данных (тип struct), содержащими разную поименованную информацию. Структурами MATLAB являются многомерные массивы, содержащие контейнеры данных, называемые полями, каждому из которых присваивается свое имя. Поля структуры могут содержать любой тип данных. Отдельная структура – это структурный массив размерности 1Х1. Допускаются два способа заполнения массива структур –операторами присваивания для всех полей каждой структуры массива, или функцией-конструктором struct, позволяющей внести значения сразу в несколько полей структуры. Можно создать структуру, а затем в любом месте добавить новое поле.
>>Human=struct('Name','Ivan','Age',28,'Sex','m');
>>Human.Info= [1 2; 3 4];
>> Human.Addres = 'Minsk';
Или:
>> Human.Name =' Ivan';
>>Human.Age= 28;
>>Human.Sex= 'm';
>> Human.Info= [11 12; 13 14];
>>Human.Addres= 'Minsk';
28.Функции для работы со структурами. fieldnames (Получение названий полей структуры), getfield (Получение содержимого определенных полей), rmfield (Удаление полей структуры), setfield (Присвоение значения полю структуры), struct (Создание структур и массива структур), struct2cell (Преобразование массива структур в ячейки), deal (Организация доступа к полям массива структур), isstruct (Проверка, является ли указанный объект структурой), isfield (Проверка, содержит указанное поле).
29. Массивы ячеек. Массив ячеек (тип cell) предназначен для хранения разнородных объектов (массивов разных размерностей, разнотипных данных). Массив ячеек состоит из ячеек, или контейнеров, каждый из которых может содержать данные разных типов. Массив ячеек может быть
полем структуры. Этот тип данных является более удобной формой организации данных по сравнению с массивом структур в том случае, когда
данные не содержат однотипных полей.
Массивы ячеек могут быть созданы либо путем последовательного присваивания значений отдельным элементам массива, либо целиком при помощи специальной функции-конструктора cell.
Как и в случае структур, кроме поэлементного создания массива ячеек,
возможно использование функции-конструктора:
>> W= cell(size(ones(2,2))) или >> W= cell(2,2);
Чтобы удалить некоторый диапазон ячеек из массива ячеек, нужно этому диапазону присвоить значение пустого массива [].
При работе с массивами ячеек важно различать ячейку (элемент массива ячеек) и ее содержимое. Выражение любого типа данных системы MATLAB можно превратить в ячейку, заключив его в фигурные скобки.
>> W = {[7 9] ' Tony ' 3+4 i ; [1 2; 3 4] - 5 ' abc '};
>> h_struct =struct('field1',[ 1 2 3],'field2','a');
>> W(1,4) = { h_struct }
Содержимое массива ячеек можно отобразить в графическом окне при помощи функции cellplot(W).
30. Доступ к ячейке и доступ к содержимому ячейки. Для того чтобы воздействовать на содержимое ячеек, нужно индексировать массив ячеек при помощи фигурных скобок. При обычной индексации круглыми скобками из массива ячеек извлекается отдельная ячейка.
31. Функции для работы с массивами ячеек. cell (Создание пустого массива ячеек заданного размера), cellfun (Применение функции к содержимому массива ячеек), cellstr (Преобразование массива символов в массив ячеек), iscellstr (Проверка, является ли объект массивом ячеек из строк), cell2struct (Преобразование массива ячеек в массив структуры), cell2matrix (Преобразование массива ячеек в матрицу), celldisp (Вывод содержимого массива ячеек в командное окно), cellplot (Отображение содержимого массива ячеек в графическом окне), num2cell (Преобразование числового массива в массив ячеек), iscell (Проверка, является ли указанный объект массивом ячеек)
32. Способы объединения строк разной длинны в массив. Для объединения строк разной длинны в массив короткие строки следует дополнить пробелами до максимальной из длин строк, входящих в массив.
>> name=['MATLAB '; 'MAPLE ';'MATHEMATICA']
Также используя функцию char:
>> name = char('MATLAB','MAPLE','MATHEMATICA');
Доступ к строкам в массиве осуществляется при помощи индексации:
>>name(1,:)
ТЕМА 3