3. Плоское движение. 4. Движение вокруг неподвижной точки. 5. Свободное движение.

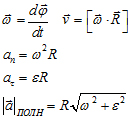
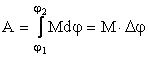Для нахождения полной работы необходимо вычислить интеграл

где  = ₂ - _1.

№ 15.Теорема Гюйгенса–Штейнера и расчет момента инерции стержня, шара, цилиндра, диска.

Теоре́ма Гю́йгенса — Ште́йнера - момент инерции тела относительно произвольной оси равен сумме момента инерции этого тела  относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями: Где  — известный момент инерции относительно оси, проходящей через центр масс тела,  — искомый момент инерции относительно параллельной оси,  — масса тела,  — расстояние между указанными осями.

Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. , где   — полная масса тела.

	Полый тонкостенный цилиндр или кольцо радиуса r и массы m	Ось цилиндра
	Сплошной цилиндр или диск радиуса r и массы m	Ось цилиндра
	Полый толстостенный цилиндр массы m с внешним радиусом r2 и внутренним радиусом r1	Ось цилиндра
	Сплошной цилиндр длины l, радиуса r и массы m	Ось перпендикулярна к цилиндру и проходит через его центр масс
	Полый тонкостенный цилиндр (кольцо) длины l, радиуса r и массы m	Ось перпендикулярна к цилиндру и проходит через его центр масс
	Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его центр масс
	Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его конец
	Шар радиуса r и массы m	Ось проходит через центр шара

№ 16. Вращение твердого тела относительно неподвижной оси. Тензор инерции. Кинетическая энергия твердого тела.

Вращением вокруг неподвижной оси называется такое движение твердого тела, при котором во все время движения две его точки остаются неподвижными. Прямая, проходящая через эти точки, называется осью вращения. Все остальные точки тела движутся в плоскостях, перпендикулярных оси вращения, по окружностям, центры которых лежат на оси вращения.

Проекция вектора угловой скорости на ось u определяется зависимостью

Скорость и ускорение точки М вращающегося твердого тела определяются соотношениями

или в скалярной форме:

Частные случаи:

1 ) равномерное вращение (ε=0):

2) равнопеременное вращение (εu=const):

Т ензор инерции — тензорная величина, связывающая момент импульса тела и кинетическую энергию его вращения с его угловой скоростью: где   — тензор инерции,   — угловая скорость,   — момент импульса. Кинетическая энергия твердого тела представляет собой сумму кинетических энергий отдельных частиц: где   - скорость центра масс тела,   - скорость i-й частицы

относительно системы координат, связанной с центром масс и совершающей поступательное движение вместе с ним. Возводя сумму скоростей в квадрат, получим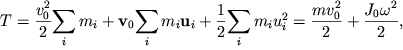

№ 17-18. Неинерциальные системы отсчета. Поступательное движение. Вращательное движение.

Неинерциа́льная систе́ма отсчёта — система отсчёта, к которой не применим закон инерции, и поэтому для согласования сил и ускорений в которой приходится вводить фиктивные силы инерции. Всякая система отсчета, движущаяся с ускорением относительно инерциальной, является неинерциальной.

Для того, чтобы найти уравнение движения в неинерциальной системе отсчёта, нужно знать законы преобразования сил и ускорений при переходе от инерциальной системы к любой неинерциальной.

Классическая механика постулирует следующие два принципа:

Время абсолютно, то есть промежутки времени между любыми двумя событиями одинаковы во всех произвольно движущихся системах отсчёта;

Пространство абсолютно, то есть расстояние между двумя любыми материальными точками одинаково во всех произвольно движущихся системах отсчёта.

Основное уравнение динамики относительного движения материальной точки имеет вид:

, где   — масса тела,   — ускорение тела относительно неинерциальной системы отсчёта,   — сумма всех внешних сил, действующих на тело,   — переносное ускорение тела,   — кориолисово ускорение тела.

Это уравнение может быть записано в привычной форме Второго закона Ньютона, если ввести фиктивные силы инерции:  — переносная сила инерции  — сила Кориолиса.

Поступательное движение — это механическое движение системы точек (тела), при котором любой отрезок прямой, связанный с движущимся телом, форма и размеры которого во время движения не меняются, остается параллельным своему положению в любой предыдущий момент времени.

Враща́тельное движе́ние — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения.

№ 19.Теорема Кориолиса. Центробежные силы.

Теорема о разложении абсолютного ускорения. Если точка движется в системе отсчета, которая в свою очередь движется относительно некоторой абсолютной системы отсчета, принимаемой за неподвижную, то абсолютное ускорение точки а_а является суммой трех ускорений: относительного ускорения ar в движущейся системе отсчета; переносного ускорения аt, т. е. ускорения той точки движущейся системы отсчета, с которой совпадает в данный момент движущаяся точка; дополнительного, так называемого поворотного ускорения, или ускорения Кориолиса аc, обусловленного взаимным влиянием вращательного движения подвижной системы отсчета и относительного движения самой точки. При этом

где Ω — угловая скорость подвижной системы отсчета и V_r — относительная скорость рассматриваемой точки.

Центробе́жная си́ла — составляющая фиктивных сил инерции, которую вводят при переходе из инерциальной системы отсчёта в соответствующим образом вращающуюся неинерциальную. Это позволяет в полученной неинерциальной системе отсчёта продолжать применятьзаконы Ньютона для расчёта ускорения тел через баланс сил.

№ 20. Закон сохранения момента импульса твердого тела.

З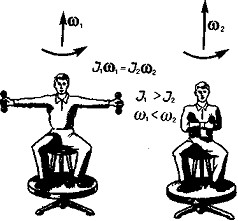 акон сохранения момента импульса — фундаментальный закон природы. Он связан со свойством симметрии пространства — его изотропностью, т. е. с инвариантностью физических законов относительно выбора направления осей координат системы отсчета (относительно поворота замкнутой системы в пространстве на любой угол).