
- •1 Коллоквиум
- •2. Цилиндрическая система координат: 3. Сферическая система координат:
- •2.Разность векторов; 3.Умножение вектора на число ; 4.Скалярное произведение векторов
- •5.Векторное произведение:
- •2 Коллоквиум
- •3. Плоское движение. 4. Движение вокруг неподвижной точки. 5. Свободное движение.
- •Вопросы домашнего конспектирования
1 Коллоквиум
№ 1. Системы отсчета, системы координат, преобразования координат
Положение тела в пространстве может быть определено только по отношению к другим телам. Тело отсчета – тело (система неподвижных тел), которое служит для определения положения интересующего нас тела.
Кроме тела отсчета нужна система, которая обеспечивала бы «адреса» других тел. С этой целью вводится система координат. Система координат позволяет определить положение тела в пространстве. Но нужна еще совокупность тела отсчета, связанных с ним координат и синхронизирующих часов – это система отсчета.
Заметим, что удачный выбор системы координат существенно облегчает решение задачи. Рассмотрим основные типы систем координат: 1. Прямоугольная Декартова: А) Двухмерная; Б) Трехмерная;

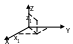
2. Цилиндрическая система координат: 3. Сферическая система координат:
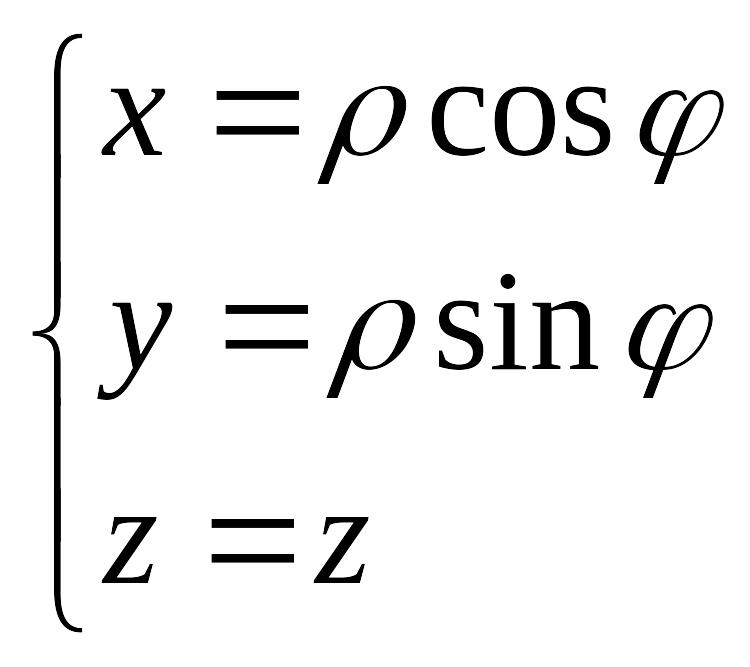

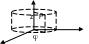
№ 2. Вектора, действия над ними, компоненты вектора, преобразование компонентов вектора, инвариантный характер вектора.
Вектор – направленный отрезок прямой, у которого один конец называется началом, а другой конец – концом. Модуль, направление, точка приложения, нулевой вектор.
Два вектора равны, если они имеют одинаковые модули и направление.
Противоположным
вектору
![]() называют вектор
называют вектор
![]() .
.
1.Сумма векторов: a.Правило треугольника ; b.Правило прямоугольника;
Если при действии над векторами результат не изменяется при перестановке векторов, то говорят, что вектора обладают свойством коммутативности относительно этого действия.
2.Разность векторов; 3.Умножение вектора на число ; 4.Скалярное произведение векторов
Скалярным произведение векторов называют произведение модулей этих векторов на косинус угла между ними. Т.е. результат скалярного произведения – скаляр.
5.Векторное произведение:
В результате векторного произведения получается вектор, модуль которого равен произведению модулей перемножающихся векторов на синус угла между ними. Результирующий вектор направлен перпендикулярно плоскости перемножаемых векторов и направлен в сторону движения правого винта, если вращать его от первого вектора ко второму по кратчайшему пути.
Компоненты векторных величин.
![]()
![]()
![]()
Орты:

Скалярные произведения одноименных орт равны 1, разноименных – 0.
Векторное произведение одноименных орт равно 0. Модуль векторного произведения разноименных орт равен 1.
Действия над векторами в координатной форме. Векторное произведение:
Радиус вектор – вектор, проведенный из начала координат в данную точку.
Угол между векторами можно вычислить, используя два способа нахождения скалярного произведения векторов.
№ 3. Скорость, ускорение прямолинейного движения.
Скорость – быстрота перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта.
Траектория
– линия, вдоль которой движется тело.
Путь – расстояние вдоль траектории![]() .
Перемещение – кратчайшее расстояние
.
Перемещение – кратчайшее расстояние![]() .
.
![]()
При прямолинейном
движении
![]() .
.
Вектором
мгновенной скорости![]() называют вектор, равный производной
радиус-вектора по времени (направлен
по касательной).
называют вектор, равный производной
радиус-вектора по времени (направлен
по касательной).
В общем случае
скорость является функцией времени,
т.е.
![]()
Ускорение в
векторной и координатной формах.![]()
вектор среднего ускорения (скорость изменения скорости)
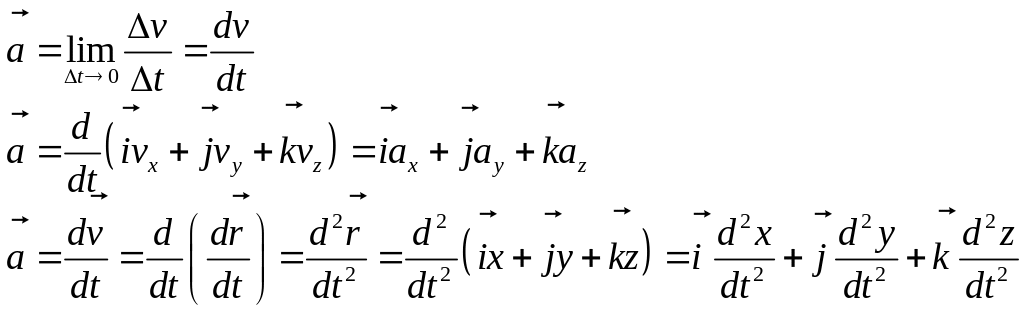
№ 4. Нормальное, тангенсальное ускорение.
Н
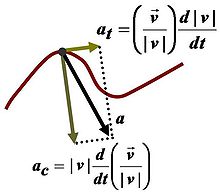 ормальное
ускорение – компонента
ускорения точки характеризующаяся
изменением направления скорости для
траектории с кривизной.
ормальное
ускорение – компонента
ускорения точки характеризующаяся
изменением направления скорости для
траектории с кривизной.
Тангенциа́льное ускоре́ние — компонент ускорения, направленный по касательной к
траектории движения. Совпадает с направлением вектора скорости при ускоренном
движении и противоположно направлено при замедленном. Характеризует изменение
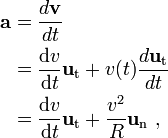 модуля
скорости.
модуля
скорости.
Компоненты ускорения при плоском движении
Выражение для тангенциального ускорения можно найти,
продифференцировав вектор скорости по времени:
где первое слагаемое — тангенциальное ускорение,
а второе — центростремительное ускорение.
№ 5. Вращательное движение, угловая скорость, ускорение, связь между угловыми и линейными величинами.
В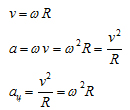 ращательное
движение – вращательное движение
твёрдого тела вокруг неподвижной оси,
при котором какие-нибудь две точки,
принадлежащие телу остаються во всё
время
ращательное
движение – вращательное движение
твёрдого тела вокруг неподвижной оси,
при котором какие-нибудь две точки,
принадлежащие телу остаються во всё
время
движения неподвижными. Прямая проведенная через них будет
называться осью вращения.
Угловая скорость – это векторная физическая величина характеризующая
скорость вращения тела.
Угловое ускорение – предел отношений изменения угловой скорости
за промежуток времени к этому промежутку времени при бесконечном
изменении последнего.
Изменение линейной скорости по направлению (меняется только направление).
В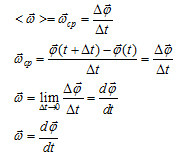 ектор
ускорения – вторая производная
вектора перемещения по времени.
ектор
ускорения – вторая производная
вектора перемещения по времени.
n – число оборотов. Если w=const, то w - круговая (циклическая) частота.
![]() Т – период (время одного оборота).
Т – период (время одного оборота).
![]() - линейная частотавращения (колебания).
- линейная частотавращения (колебания).
Модуль
![]() равен углу поворота и направлен по оси
вращения так,
равен углу поворота и направлен по оси
вращения так,
что направление
поворота отвечает правилу винта.
![]() - угловое ускорение.
- угловое ускорение.

При равноускоренном
движении вектор
направлен в ту же сторону что и
![]() .
.
При равнозамедленном – в обратную.
№ 6. Преобразования Галилея, сложение скоростей.
В момент t=0 начала систем отсчета совпадают,
а в момент tK’ находится в точке
момент t=0 начала систем отсчета совпадают,
а в момент tK’ находится в точке
![]() .
.
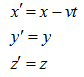
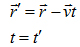
Величины, численные значения которых не изменяются при преобразованиях – инварианты. При преобразованиях изменяются варианты (скорость, импульс, координаты).
![]() Его длина в неподвижной системе отсчета:
Его длина в неподвижной системе отсчета:
![]()
Сложение скоростей
В штрихованной:
![]() В не штрихованной:
В не штрихованной:
![]()
![]()
Так как
![]()

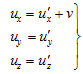 -
формулы сложения скоростей в
нерелятивистской механике.
-
формулы сложения скоростей в
нерелятивистской механике.
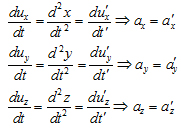
![]() -
-
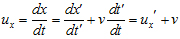 ускорение инвариантно.
ускорение инвариантно.
№ 7. Преобразования Лоренца, инварианты преобразований.
Преобразования Лоренца − преобразования координат и времени какого-либо события при переходе от одной инерциальной системы отсчёта к другой.
Преобразования Лоренца отражают равноправие всех инерциальных систем отсчёта в описании законов природы. Если инерциальная система отсчёта K' движется относительно инерциальной системы отсчёта K с постоянной скоростью v вдоль оси x, то преобразования Лоренца имеют вид
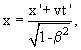 y = y', z = z'
y = y', z = z'
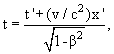 c - скорость света в вакууме, β = v/c.
c - скорость света в вакууме, β = v/c.
При V меньшей С преобразования Лоренца переходят в преобразования Галилея x = x' + vt, y = y', z = z', t = t'.
И з
преобразований Лоренца следует, что
промежутки времени Δt и отрезки длины
Δl зависят от движения системы отсчёта.
Если в системе K' два события, происходящие
в одном и том же месте, разделены
интервалом времени Δt', то в системе K
эти же происходящие в разных местах
з
преобразований Лоренца следует, что
промежутки времени Δt и отрезки длины
Δl зависят от движения системы отсчёта.
Если в системе K' два события, происходящие
в одном и том же месте, разделены
интервалом времени Δt', то в системе K
эти же происходящие в разных местах
события разделены промежутком времени Δt
Е![]() сли
отрезок, покоящийся в системе K', имеет
длину Δl', то его длина Δl в системе
сли
отрезок, покоящийся в системе K', имеет
длину Δl', то его длина Δl в системе
K, принимает значение
Поперечные размеры тел при этом не изменяются. Формулы преобразования скорости:
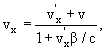
![]()
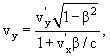
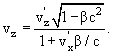
Инвариантом при преобразовании Лоренца является также квадрат 4-вектора энергии-импульса
№ 8. Опыты по определению постоянства скорости света.
Идея опыта состоит в сравнении прохождения светом двух путей, из которых один совпадает с направлением движения тела в эфире, а другой ему перпендикулярен. Пластинка B полупрозрачна. На ней луч разделяется на два когерентных перпендикулярных луча, идущих к зеркалам D и C, после отражения от зеркал светоделитель вновь их объединяет на пути BE.
Если эти пути пройдены ими за одинаковое время, то в точку встречи они придут в одной фазе и усилят друг друга. Если за разное время, то в точке встречи разность фаз и колебаний изменится. Наблюдая интерференцию, можно сделать вывод о разности фаз пришедших в интерферометр когерентных волн, а отсюда вычислить время запаздывания одной волны относительно другой. Пусть прибор движется в направлении плеча BC со скоростью v относительно эфира. Скорость света относительно эфира c.

№ 9. Кинематические следствия из преобразований Лоренца.
Относительность одновременности и принцип причинности.
Инвариантность интервала.
Сокращение длин и изменение формы движущихся тел.
Собственное время. Замедление хода движущихся часов.
Сложение скоростей и преобразование ускорений.
№ 10. Инварианты в преобразованиях Лоренца, 4-х мерный интервал.
Инвариантом между событиями является величина S, квадрат которой определяется по формуле:
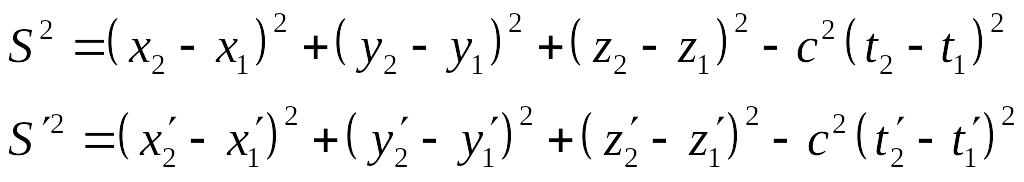
Интервал, определяя пространственно временные соотношения между событиями, является инвариантом при переходе от одной системы к другой.
Преобразования Лоренца |
Преобразования Галилея |
||
Инвариантные |
Вариантные |
Инвариантные |
Вариантные |
|
|
|
Координаты
|
Собственное время – инвариант относительно преобразований Лоренца.
![]() -
дифференциал собственного времени
движущейся точки.
-
дифференциал собственного времени
движущейся точки.
![]() -
дифференциал времени той инерциальной
системы отсчета, в которой данная точка
имеет скорость
-
дифференциал времени той инерциальной
системы отсчета, в которой данная точка
имеет скорость
![]() .
.
№ 11. Собственное время, замедление хода движения часов, опыт Хафеля.
Собственное время в теории относительности, время, измеряемое часами в собственной системе отсчёта движущегося тела, т. е. часами, жёстко связанными с телом (покоящимися относительно него и находящегося в том же месте).
Под релятиви́стским замедле́нием вре́мени обычно подразумевают кинематический эффект специальной теории относительности, заключающийся в том, что в движущемся теле все физические процессы проходят медленнее, чем следовало бы для неподвижного тела по отсчётам времени неподвижной (лабораторной) системы отсчёта.
Релятивистское замедление времени проявляется, например, при наблюдении короткоживущих элементарных частиц, образующихся в верхних слоях атмосферы под действием космических лучей и успевающих благодаря ему достичь поверхности Земли.
Количественное описание замедления времени может быть получено из преобразований Лоренца:
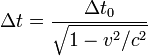 где
где ![]() —
время, проходящее между двумя событиями
движущегося объекта с
—
время, проходящее между двумя событиями
движущегося объекта с
точки зрения неподвижного
наблюдателя, ![]() —
время, проходящее между двумя
—
время, проходящее между двумя
событиями движущегося
объекта с точки зрения наблюдателя,
связанного с движущимся объектом, ![]() —
относительная скорость движения
объекта,
—
относительная скорость движения
объекта, ![]() —
скорость света в вакууме.
—
скорость света в вакууме.
Опыт Хафеля
Дважды облетели вокруг света, сначала на восток, затем на запад, с четырьмя комплектами цезиевых атомных часов, после чего сравнили «путешествовавшие» часы с часами, остававшимися в Военно-морской обсерватории США. В системе отсчёта, покоящейся относительно центра Земли, часы на борту самолёта, движущегося на восток (в направлении вращения Земли), идут медленнее, чем часы, которые остаются на поверхности, а часы на борту самолёта, движущегося в западном направлении (против вращения Земли), идут быстрее.
№
12. Сложение скоростей
по Галилею и Лоренцу.
![]()
Можно
заметить, что в случае, когда
![]() ,
преобразования
Лоренца переходят в преобразования
Галилея. Это говорит о том, что
специальная теория относительности
совпадает с механикой
Ньютона при скоростях, малых по
сравнению со скоростью света. Это
объясняет, каким образом сочетаются
эти две теории — первая является
уточнением второй.
,
преобразования
Лоренца переходят в преобразования
Галилея. Это говорит о том, что
специальная теория относительности
совпадает с механикой
Ньютона при скоростях, малых по
сравнению со скоростью света. Это
объясняет, каким образом сочетаются
эти две теории — первая является
уточнением второй.
№ 13. Первый и второй законы Ньютона, масса, инертность, инерция.
П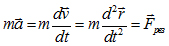 ервого
закона Ньютона (закона
инерции) - существуют
такие системы отсчета, относительно
которых тело (материальная точка) при
отсутствии на нею внешних воздействий
(или при их взаимной компенсации)
сохраняет состояние покоя или равномерного
прямолинейного движения.
ервого
закона Ньютона (закона
инерции) - существуют
такие системы отсчета, относительно
которых тело (материальная точка) при
отсутствии на нею внешних воздействий
(или при их взаимной компенсации)
сохраняет состояние покоя или равномерного
прямолинейного движения.
Второй закон Ньютона - сила, действующая на тело, равна произведению
массы тела на ускорение, сообщаемое этому телу силой.
Ф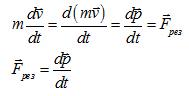 изическое
содержание этого закона состоит в том,
что сила
изическое
содержание этого закона состоит в том,
что сила
определяет вторые производные координат по времени.
Масса тела, являющаяся характеристикой его инерционных и
гравитационных свойств, представляет собой величину, зависящую только
от самого тела и не зависящую от того, в каких именно взаимодействиях
с другими телами это тело участвует. Однако масса зависит от скорости
движения тела. Инерция - явление сохранения телом состояния покоя или прямолинейного равномерного движения при отсутствии или компенсации внешних воздействий на это тело.
Инертность - свойство тела сохранять свою скорость неизменной, т. е. сохранять состояние покоя или равномерного прямолинейного движения при отсутствии внешних воздействий на это тело или их взаимной компенсации.
№ 14. Интерпретация третьего закона Ньютона, при электромагнитном взаимодействии движущихся зарядов.
Рассмотрим взаимодействие двух зарядов.
Равенство сил не выполняется. Сумма импульсов зарядов не сохраняется.
Во взаимодействии участвуют не только заряды, но и поля E и B.
В электродинамике показывается, что поля E и B имеют плотность импульса (импульс, отнесенный к единице объема).
Вычисления показывают, что суммарный импульс, создаваемый зарядами и их электромагнитными полями, сохраняется. Вот почему формулировка третьего закона в виде сохранения импульсов более физически содержательна.
ТРЕТИЙ ЗАКОН: определяет характер взаимодействия тел.
Силы взаимодействия 2-ух материальных точек равны по величине и противоположны по направлению, и действуют вдоль прямых объединяющих эти точки.

![]()
№![]() 15. Продольная, поперечная масса,
релятивистская масса.
15. Продольная, поперечная масса,
релятивистская масса.
П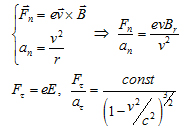 родольная
и поперечная масса. Сила действует на
заряженную частицу
родольная
и поперечная масса. Сила действует на
заряженную частицу
![]() массой
массой
![]() .
.
При малой скорости
мы должны получить
![]() (масса
(масса
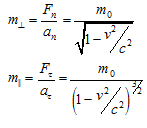 покоя при нулевой скорости).
покоя при нулевой скорости).
Следовательно, инертность частицы по направлению
скорости
![]() отличается от
отличается от![]() .
.
Р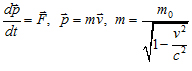 елятивистское
уравнение движения.
елятивистское
уравнение движения.
 где m –
релятивистская масса.
где m –
релятивистская масса.
№ 16. Момент силы, момент импульса, уравнение движения материальной точки.
Момент
силы — векторная физическая
величина,
равная векторному произведению радиус-вектора,
(проведенного от оси вращения к
точке приложения силы —
по определению), на вектор этой силы.
Характеризует вращательное действие
силы на твёрдое тело.
![]()
где ![]() —
сила, действующая на частицу,
а
—
сила, действующая на частицу,
а ![]() — радиус-вектор частицы.
— радиус-вектор частицы.
М![]() оме́нт
и́мпульса -
характеризует количествовращательного
движения.
Величина, зависящая от того,
сколько массы вращается,
как она распределена относительно оси
вращения и с какой скоростью
происходит вращение.
оме́нт
и́мпульса -
характеризует количествовращательного
движения.
Величина, зависящая от того,
сколько массы вращается,
как она распределена относительно оси
вращения и с какой скоростью
происходит вращение.
где ![]() —
радиус-вектор частицы относительно
выбранного неподвижного в данной системе
отсчёта начала,
—
радиус-вектор частицы относительно
выбранного неподвижного в данной системе
отсчёта начала, ![]() —
импульс частицы.
—
импульс частицы.
Уравнение
движения запишется так:![]()
№ 17. Основные уравнения механики, системы материальных точек, центр масс, уравнения моментов для системы материальных точек. Теорема о движении центра масс.
Системой материальных точек называется такая их совокупность, в которой положение и движение каждой точки зависит от положения и движения всех точек данной системы.
Внешние силы – силы, источники которых лежат вне системы.
Внутренние силы – силы, источники которых лежат внутри системы.
Точку пересечения линий действия сил, вызывающих поступательное движение тела, называют центром масс этого тела. Такое название не случайно. Центр масс является точкой, характеризующей распределение масс в данном теле (или в механической системе). Положение центра масс зависит от того, как распределяется по объему тела его масса. Центр масс не обязательно должен находиться в самом теле.
Уравнение движения системы материальных точек: Продифференцируем равенство
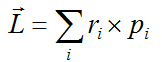


Теорема о движении центра
масс.Центр масс механической
системы движется как
материальная точка с массой,
равной массе всей системы,
под действием всех
приложенных к точкам
системы внешних сил.
№ 18. Работа. Работа постоянной и переменной силы. Потенциальное поле сил.
Работа – это физическая величина, являющаяся скалярной количественной мерой действия силы на тело или систему, зависящая от численной величины, направления силы и от перемещения точки тела или системы.
Работа постоянной силы – это скалярное произведение вектора силы на перемещение, которое совершило тело под действием силы. A = (F ⋅ ∆r) = F ⋅ ∆r ⋅ cosα.
Работа переменной силы Если величина силы не остается постоянной во время движения, то для вычисления
работы следует весь путь S разбить на элементарные отрезки ∆S, настолько малые, чтобы величину силы на этом участке можно было считать постоянной. Переменная работа вычисляется как сумма элементарных работ.
№ 19. Потенциальная энергия. Изменение потенциальной энергии за счет работы сил: Силы тяжести; Силы упругости; Силы гравитации; Силы трения;
Потенциальная энергия ![]() — скалярная физическая
величина,
характеризующая способность некого
тела совершать работу за
счет своего нахождения в поле действия
сил.
— скалярная физическая
величина,
характеризующая способность некого
тела совершать работу за
счет своего нахождения в поле действия
сил.
![]()
№20 . Нормировка потенциальной энергии. Градиент. Понятие градиента, физический смысл.
Если вместо
![]() взять другую функцию
взять другую функцию
![]() ,
то есть измененную на всем пространстве,
то сила не изменится.
,
то есть измененную на всем пространстве,
то сила не изменится.
![]()
Потенциальная энергия определена с точностью до постоянной.
Процедура придания потенциальной энергии однозначности называется нормировкой.
Градиент -
вектор,
своим направлением указывающий
направление наискорейшего возрастания
некоторой величины ![]() ,
значение которой меняется от одной
точки пространства к другой, а по величине
равный быстроте роста этой величины в
этом направлении.
,
значение которой меняется от одной
точки пространства к другой, а по величине
равный быстроте роста этой величины в
этом направлении.
Градиент функции есть вектор, направленный по нормали к поверхности уровня в сторону возрастания U, его длина равна по нормам функции к той же поверхности.
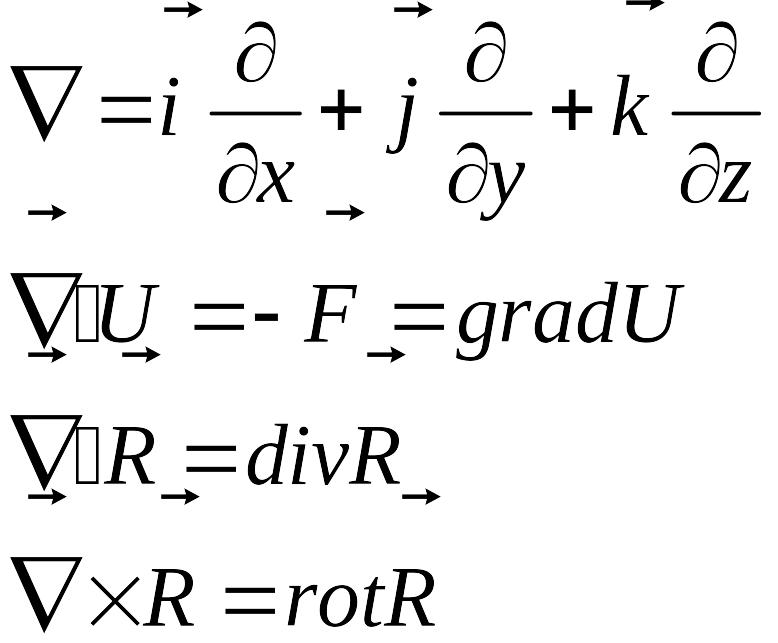
Величина v/x называется градиентом скорости и показывает, как быстро меняется скорость при переходе от слоя к слою в направлении х, перпендикулярном направлению движения слоев.
№ 21. Кинетическая энергия .
Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек.
Поступательное движение — это механическое движение системы точек (тела), при котором любой отрезок прямой, связанный с движущимся телом, форма и размеры которого во время движения не меняются, остается параллельным своему положению в любой предыдущий момент времени.
Враща́тельное движе́ние — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения.

Работа силы при поступательном движении материальной точки равна приращению кинетической энергии этой точки.
№ 22. Законы сохранения импульса и момента импульса .
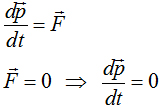 Импульс изолированной системы
не изменяется при любых процессах
происходящих внутри
Импульс изолированной системы
не изменяется при любых процессах
происходящих внутри
Системы.
В релятивистском случае: так как не существует центра масс, то его нельзя интерпретировать
движение системы как равномерное и прямолинейное движение центра масс. Т.е. не
 существует системы
отсчета центра масс, в котором импульс
равен 0.
существует системы
отсчета центра масс, в котором импульс
равен 0.
Закон сохранения момента импульса Для изолированной системы:
В инерциальной системе отсчета момент импульса изолированной
системы остается постоянным при любых процессах, происходящих внутри
системы. У незамкнутых систем может сохраняться не сам момент импульса
а его проекция на некоторую неподвижную ось. Например, если система
движется в
однородном поле силы тяжести вертикальной
оси
![]()
№ 23. Закон сохранения энергии. Не релятивистский случай.
Примеры:
1)реактивное движение
2)распад атома с испусканием фотона. В данном случае, исходя из закона сохранения импульса.
Закон сохранения энергии в нерелятивистском случае
П![]() усть
m0 движется под действием F.
усть
m0 движется под действием F.
Умножив на v, получаем:
![]() но
но
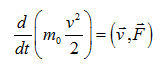 или
или
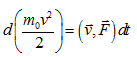 Проинтегрируем:
Проинтегрируем:
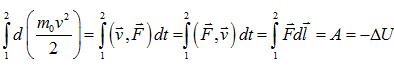
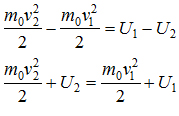 и
получим:
и
получим:
То есть сумма кинетической и потенциальной энергий
п![]() ри
движении остается постоянной.
ри
движении остается постоянной.
Пример: Одномерное движение.
№ 24. Закон сохранения энергии. Релятивистский случай.
Р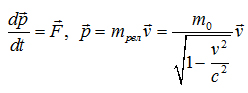
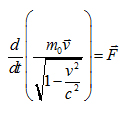 ассуждения
относительно работы сил, потенциальности
сил и потенциальной энергии справедливы
и в случае скоростей, близких к скорости
света.
ассуждения
относительно работы сил, потенциальности
сил и потенциальной энергии справедливы
и в случае скоростей, близких к скорости
света.
Воспользуемся релятивистским уравнением движения.
Умножим скалярно на v:
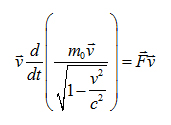
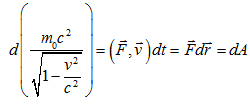
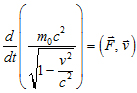
Сравним с нерелятивистским случаем:
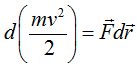
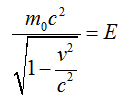 То есть, вместо
кинетической энергии в результате
совершения работы изменяется
То есть, вместо
кинетической энергии в результате
совершения работы изменяется
Величина.
 Полная энергия
движущегося тела -
Полная энергия
движущегося тела -
Если поле потенциальных сил U, то
Закон сохранения энергии в
релятивистском случае.
Если v=0, то
![]() ,
то есть энергия покоя. Если тело покоится,
то его энергия не равна 0.
,
то есть энергия покоя. Если тело покоится,
то его энергия не равна 0.
Т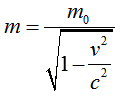 о
есть, тело обладает энергией, обусловленной
наличием массы.
о
есть, тело обладает энергией, обусловленной
наличием массы.
Масса растет со скоростью -
Можно предполагать связь массы и кинетической энергии.
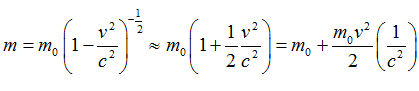 или
или
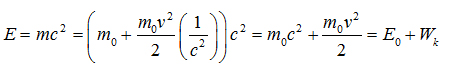
То есть, полная энергия равна кинетической энергии и энергии покоя.
![]() - приращение энергии пропорционально
ее релятивистской массы.
- приращение энергии пропорционально
ее релятивистской массы.
№ 25. Закон взаимодействия массы и энергии.
В обычных условиях изменения в энергии приводят к очень малым изменениям в массе: почти никогда не удается из данного количества вещества извлечь много энергии; но в атомной бомбе с энергией взрыва, эквивалентной 20 000 тонн тринитротолуола, весь пепел, осевший после взрыва, на 1 г легче первоначального количества расщепляющегося материала. Это потому, что выделилась энергия, которая имела массу 1 г, в согласии с формулой ΔЕ = Δ(mс2). Вывод об эквивалентности массы и энергии прекрасно подтвердился в опытах по аннигиляции материи — превращению вещества в энергию. Электрон с позитроном могут взаимодействовать в покое, имея каждый массу покоя m0. При сближении они исчезают, а вместо них излучаются два γ-луча, каждый опять с энергией m0с2. Этот опыт прямо сообщает нам о величине энергии, связанной с существованием массы покоя у частицы.

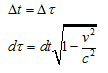 Скорости
Скорости