16.15. Асимптоты графика функции

Определение 16.5. Прямая L называется асимптотой кривой, заданной уравне-нием , если расстояние между точками кривой и прямой стремится к нулю с удалением точки на кривой от начала координат.

Асимптоты могут быть вертикальными, наклонными и горизонтальными.

Вертикальная асимптота

Прямая является вертикальной асимптотой, если точка – есть точка разрыва второго рода функции , т.е. если хотя бы один из односторонних пределов равен бесконечности.

Наклонная и горизонтальная асимптоты

Прямая называется наклонной асимптотой графика непрерывной функции при или , если

.

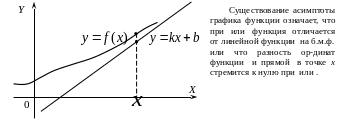
Укажем способ определения коэффициентов k и b наклонной асимптоты .

Теорема 16.19. Для того чтобы прямая являлась наклонной асимпто-той графика функции при или , необходимо и достаточно существование конечных пределов:

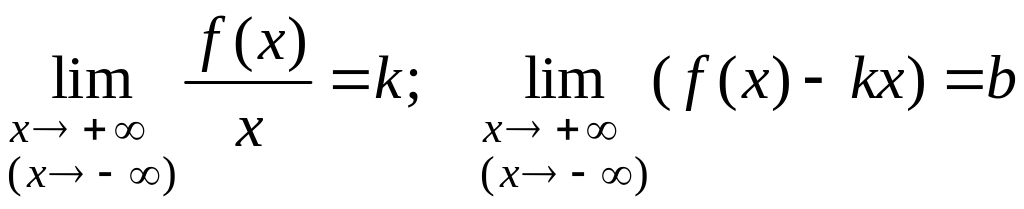. (16.17.)

Доказательство. Для доказательства ограничимся случаем, когда .

Необходимость. Если – асимптота графика функции при , то из условия имеем:

и

.

Достаточность. Пусть существуют пределы (15.17.). Тогда из второго равенства по теореме о связи функции, ее предела и б.м.ф. получаем:

, откуда , т.е. прямая – наклонная асимптота графика функции при . 

В частности, если , то . Поэтому прямая – уравнение горизонтальной асимптоты.

Пример 16.25. Найти асимптоты графика функции:

.

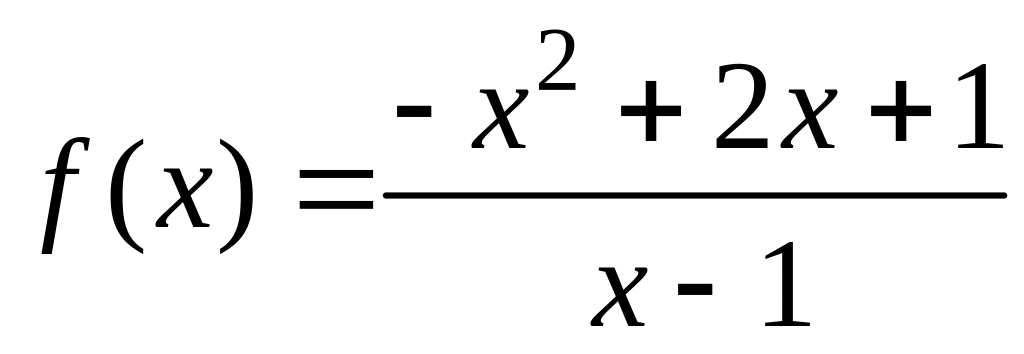Решение. При функция не ограничена, следовательно, вертикальной асимптотой будет прямая .

Далее, согласно формулам (16.17.), находим:

;

.

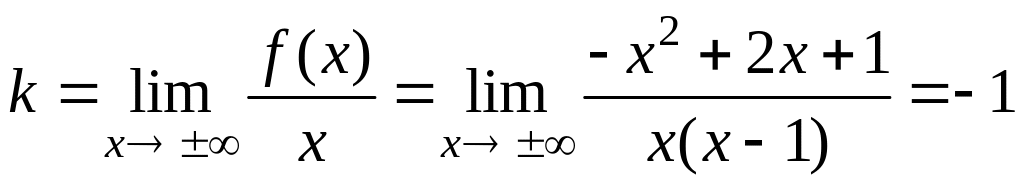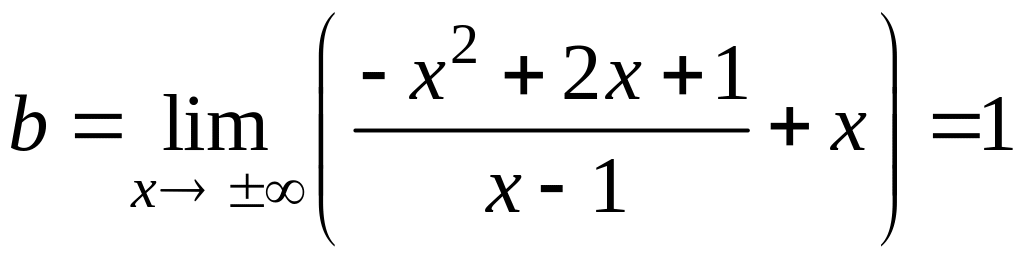т.е. наклонная асимптота задается уравнением . 

16.16. Общая схема исследования и построения графика

Исследование функции целесообразно вести в определенной последова-тельности.

Примерный план исследования функции

1) Находим область определения функции.

2) Исследуем функцию на периодичность; четность или нечетность.

3) Находим (если это возможно) точки пересечения с осями координат.

4) Исследуем функцию на монотонность и точки экстремума.

5) Находим промежутки выпуклости, вогнутости и точки перегиба.

6) Находим асимптоты графика функции.

7) Для уточнения хода графика функции (если в этом есть необходимость) находим дополнительные точки.

8) По полученным данным строим график функции.

16.17. Формула Тейлора

Одной из основных задач математического анализа является задача приближения или аппроксимации функции в окрестности данной точки, которая часто называется рабочей точкой. Наиболее простыми функциями являются многочлены. Возникает вопрос о возможности аппроксимации данной функции в окрестности рабочей точки много-членом некоторой степени. Для дифференцируемых функций эта проблема решается с помощью формулы Тейлора.

Как уже известно, приращение функции в точке x можно представить в виде , где при . Тогда, согласно этой формуле дифференцируемую функцию в окрестности точки можно представить в виде:

или

,

т.е. существует многочлен первой степени , такой, что при имеет место равенство , причем многочлен удовлетворяет условиям , .

Поставим более общую задачу. Пусть функция определена в некоторой окрестности точки и имеет в этой точке n производных . Попытаемся найти многочлен степени не выше n, такой, что

, (16.18.)

где удовлетворяет условиям

,

, (16.19.)

………….,

.

Будем искать многочлен в виде

. (16.20.)

Отсюда, дифференцируя, последовательно находим:

;

;

;

……………………………….

.

Используя теперь условие (16.19.), получаем:

 ;

 ;

 ;

 ;

…………………………………

 .

Таким образом, значения коэффициентов многочлена определены. Подставим их в равенство (16.20.) и получим многочлен

. (16.21.)

Формула (16.21.) называется многочленом Тейлора степени n функции .

Рассмотрим функцию . Функция представляет собой погрешность при замене функции многочленом в окрестности точки . Функция называется остаточным членом, который имеет несколько представле-ний:

при – остаточный член в форме Пеано;

, где – остаточный член в форме Лагранжа.

Таким образом, .

Сформулируем теорему (без доказательства), в которой введем формулу, позво-ляющую, в определенных условиях, приближенно представить функцию в виде многочлена и дать оценку погрешности этого приближения.

Теорема 16.20. Если функция определена в некоторой окрестности точки и имеет в ней производную до (n+1)-го порядка включительно, то для любого x из этой окрестности найдется точка такая, что справедлива формула

, (16.21.)

где .

Формула (16.21.) называется формулой Тейлора n-го порядка с остаточным членом в форме Лагранжа.

Если , то формула (16.21.) называется формулой Маклорена и она имеет вид:

, (16.22.)

где .

Пример 16.26. Разложить по формуле Тейлора функцию в окрестности точки .

Решение. Последовательно находим: ;

 ;

 ;

 ;

при .

Таким образом,

.

Многочлен третьей степени представлен в виде многочлена Тейлора по степени . 