16.11. Правило Лопиталя

Во многих случаях отыскание предела функции в точке или на бесконечности приводит к неопределенностям вида , , , , , , , для раскрытия которых можно использовать понятие производной. Введем правило Лопиталя.

Теорема 16.10. (Правило Лопиталя раскрытия неопределенности )

Пусть функции и непрерывны и дифференцируемые в окрестности точки . Пусть и в указанной окрестности и , . Тогда, если существует (конечный или бесконечный), то существует и имеет место равенство

. (16.15.)

Доказательство. Доопределим функции и в точке , полагая . Тогда они будут непрерывны в точке . Применим к ним теорему Коши на отрезке и получим

,

где точка c удовлетворяет условию или . Если , то поэтому, согласно условию теоремы,

.



Коротко полученную формулу читают так: предел отношения двух бесконечно малых равен пределу отношения их производных, если последний существует.

Замечания. 1) Теорема 16.10. справедлива и в том случае, когда . Действи-тельно, положив , получим

.

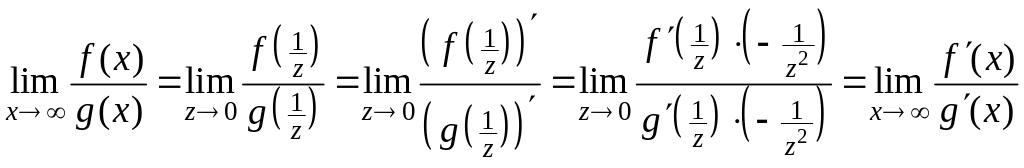2) Если производные и удовлетворяют тем же условиям, что и функции и теорему 16.10. можно применить еще раз:

и т.д.

Пример 16.17. Найти .

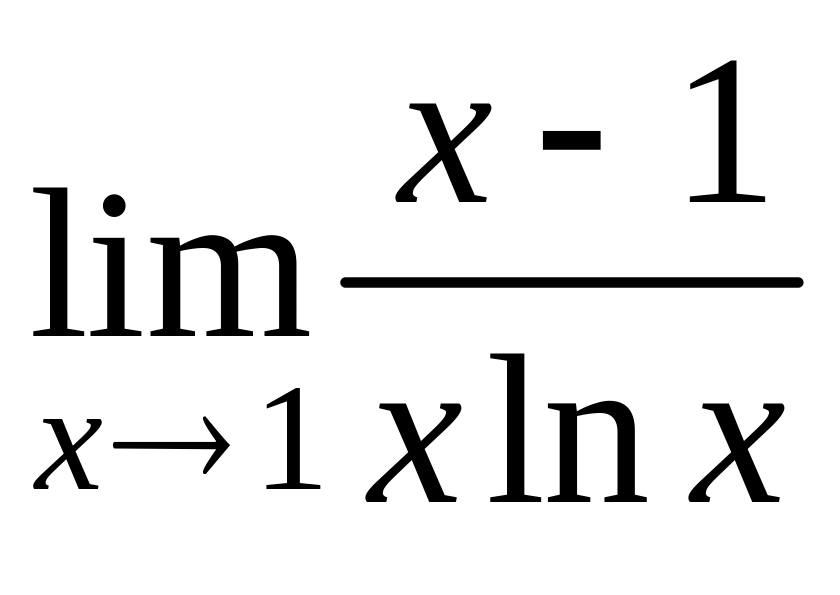Решение. .



Теорема 16.10. дает возможность раскрыть неопределенность вида . Сформу-лируем без доказательства теорему о раскрытии неопределенности вида .

Теорема 16.11. (Правило Лопиталя раскрытия неопределенности )

Пусть функции и непрерывны и дифференцируемые в окрестности точки (кроме, может быть, точки ), в этой окрестности , , и . Тогда, если существует (конечный или бесконечный), то существует и имеет место равенство

. (16.16.)

Пример 16.18. Найти .

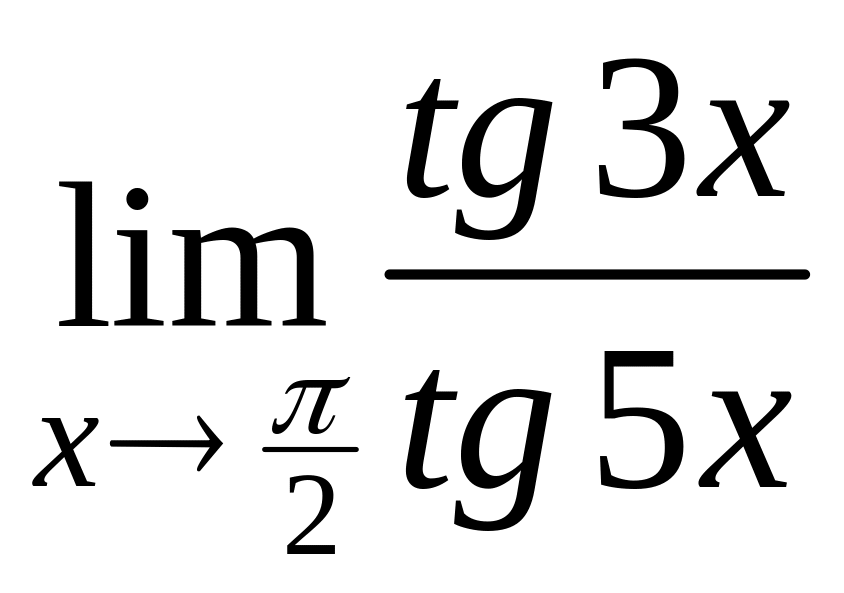Решение. Способ 1.

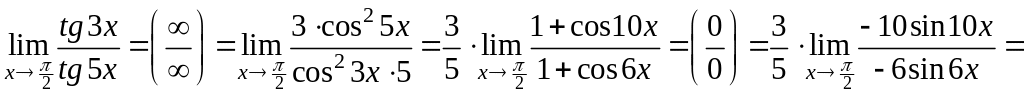
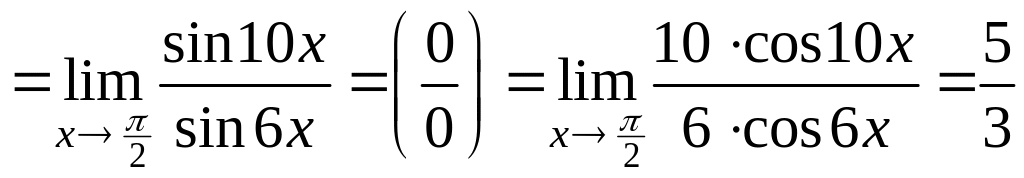
Способ 2.

.



Пример 16.19. Найти .

Решение.

.



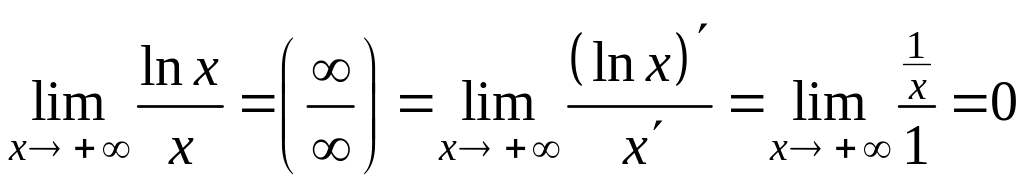Раскрытие неопределенностей различных видов

Правило Лопиталя применяется для раскрытия неопределенностей вида и , которые называют основными. Неопределенности вида , , , , сводятся к двум основным видам путем тождественных преобразований.

1. Пусть при . Тогда очевидны следующие преобра-зования:

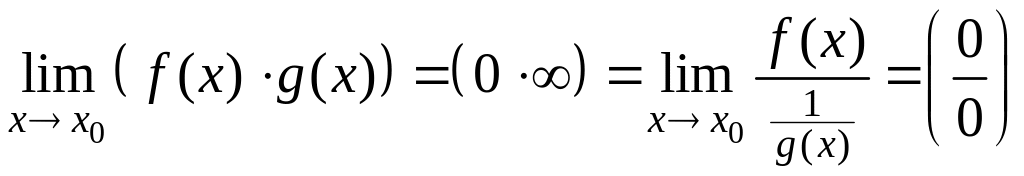или .

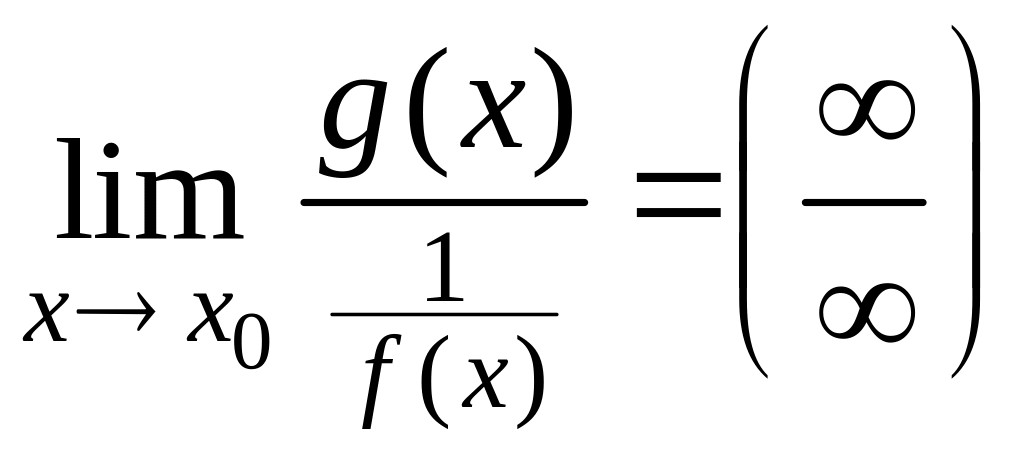Например,

.

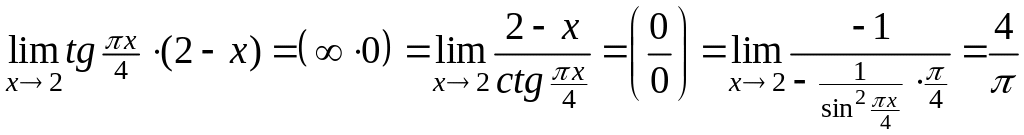2. Пусть при . Тогда можно поступить так:

.

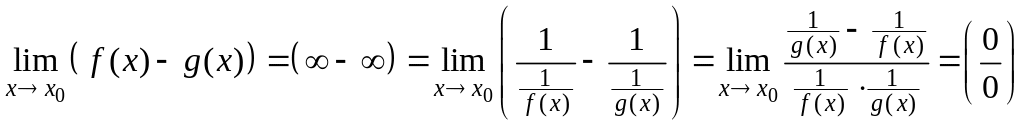Например,

.

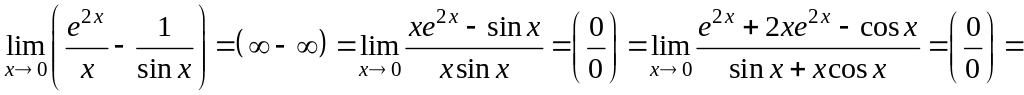
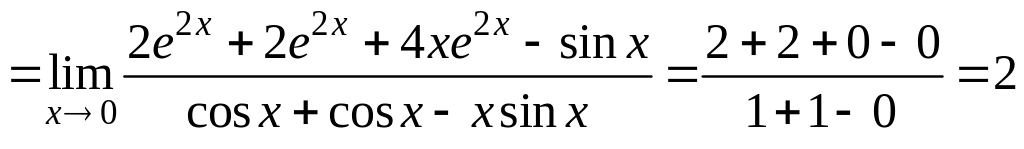3. Пусть и , или и , или и при . Для нахождения предела вида удобно сначала прологарифмировать выражение .

Пример 16.20. Найти .

Решение. Имеем неопределенность вида . Логарифмируем выражение , получаем или . Затем находим предел:

,

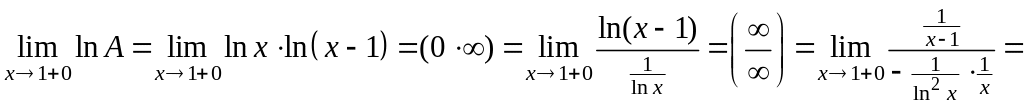
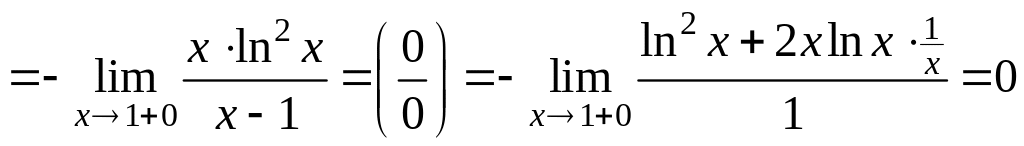т.е. . Следовательно, .

Отсюда , и .



Решение можно оформить короче, если воспользоваться «готовой» формулой:

.

16.12. Возрастание и убывание функций

Процессы, происходящие в механике, физике, химии, термодинамике, экономике, очень часто описываются функциями, заданными формулами. Чтобы знать характерис-тики рассматриваемого процесса, следует изучить характеристики функций, описы-вающих процесс, а для наглядности рассмотреть функции в их графическом задании. Но чаще интерес представляет не графическое задание функции, а качественное поведение графика функции без соблюдения масштабных размеров для достаточно точного (прибли-женного с заданной точностью) определения значений функции. Эти качественные свойства функций можно описать, используя методы дифференциального исчисления.

Теорема 16.12. (условие монотонности функции) Пусть функция определена на X и внутри имеет конечную производную . Для того чтобы была монотонно возрастающей (убывающей), достаточно, чтобы ( ) для всех x внутри X.

Доказательство. Возьмем промежуток так, чтобы , и применим к функции на этом промежутке формулу Лагранжа:

,

где .

Если и , то . Следовательно, функция возрастает.

Если и , то . Следовательно, функция убывает.



Если функция , определенная и непрерывная на множестве X, не является монотонной, то найдутся такие части промежутка X, что наибольшее или наименьшее значение достигается функцией во внутренней точке.

Определение 16.3. Функция имеет в точке максимум (минимум), если существует такая окрестность точки , не выходящая из области определения функции, что для всех

.

Максимум и минимум называют общим термином «экстремум».

Из определения экстремума следует, что вне окрестности точки максимума значения функции могут быть больше этого максимума. Поэтому такой максимум назы-вается локальным (местным). Аналогично определяется локальный минимум. Точки локального максимума и минимума называются точками локального экстремума, а значе-ния функции в них – локальными экстремумами функции.

Если функция определена на отрезке и имеет локальный экстремум на каком-то из концов этого отрезка, то такой экстремум будем называть локальным односторонним или краевым экстремумом. В этом случае соответствующая окрестность является правой для a и левой для b полуокрестностью.

Рассмотрим условия существования экстремума функции. Необходимое условие экстремума примем без доказательства.

Теорема 16.13. (необходимое условие экстремума) Если дифференцируемая функция имеет экстремум в точке , то ее производная в этой точке равна нулю: .

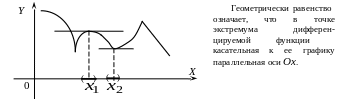
Отметим, что обратная теорема неверна, т.е. если , то это не значит, что – точка экстремума.

Точки, в которых производная равна нулю, называются стационарными (крити-ческими или «подозрительными» на экстремум). Точки, в которых функция непре-рывна, но производная не существует или бесконечна, также являются критическими, так как это тоже точки, где может быть экстремум.

Например, для функции ее производная равна нулю при , но не является точкой экстремума. Непрерывная функция в точке производной не имеет, но точка – точка минимума.

Теорема 16.14. (первое достаточное условие экстремума) Пусть точка – критическая, т.е. или не существует. Предположим, что в некоторой окрестности для существует конечная производная и она сохраняет свой знак слева и справа от . Тогда:

1) если при и при , т.е. при переходе через производная изменяет знак с «+» на «», то в точке функция имеет максимум;

2) если при и при , т.е. при переходе через производная изменяет знак с «» на «+», то в точке функция имеет минимум;

3) если при переходе через знак производной не изменяется, то экстре-мума в точке нет.

Доказательство. Действительно, в первом случае на возрастает, а на убывает, т.е. в точке функция имеет максимум. 

Теорема 16.15. (второе достаточное условие экстремума) Если – крити-ческая точка, т.е. , и функция в точке имеет вторую производную , то в случае функция имеет в точке максимум, а при – минимум.

Доказательство. Если существует, то существует в точке и в некоторой ее окрестности . Тогда

.

Если , то и при получаем , т.е. возрастает, а при , т.е. убывает.

Таким образом, при переходе через производная изменяет знак с отрицательного на положительный и в точке функция имеет минимум.

Пусть , тогда . При , а при следовательно, имеем максимум. 

Надо отметить, что т. 16.15. не применима, если или не существует.

Пример 16.21. Найти точки экстремума и промежутки возрастания и убывания для функции:

.

Решение. Функция определена и дифференцируема на . Ее производная равна . Необходимое условие экстремума: . Имеем . Получили две критические точки, которые разбивают всю область определения на три интервала . Применим первое достаточное условие экстремума, т.е. на рисунке отметим знаки первой производной и стрелками поведение функции на каждом интервале

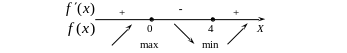
Точка – точка максимума. .

Точка – точка минимума. .

На интервалах и , следовательно, функция возрастает, на интервале – функция убывает.

II способ.

Вместо исследования перемены знака первой производной можно найти значения второй производной в критических точках: . , т.е. в точке вторая производная отрицательна, то в этой точке функция имеет максимум, а если в точке вторая производная положительна, то в этой точке функция имеет минимум. 