Приближенные вычисления с помощью дифференциала

Как уже известно, приращение функции в точке x можно представить в виде , где при , или . Отбрасывая бесконечно малую более высокого порядка, чем , получаем приближенное равенство

,

причем это равенство тем точнее, чем меньше .

Это равенство позволяет с большой точностью вычислить приближенно прира-щение любой дифференцируемой функции.

Дифференциал обычно находится значительно проще, чем приращение функции, поэтому эта формула широко применяется в вычислительной практике.

Подставляя в равенство значения и , получаем

или

(16.12.)

Формула (16.12.) используется для вычислений приближенных значений функции.

Пример 16.15. Вычислить приближенно .

Решение. Рассмотрим функцию ;

, где .

Находим первую производную функции и значение первой производной в точке .

;

.

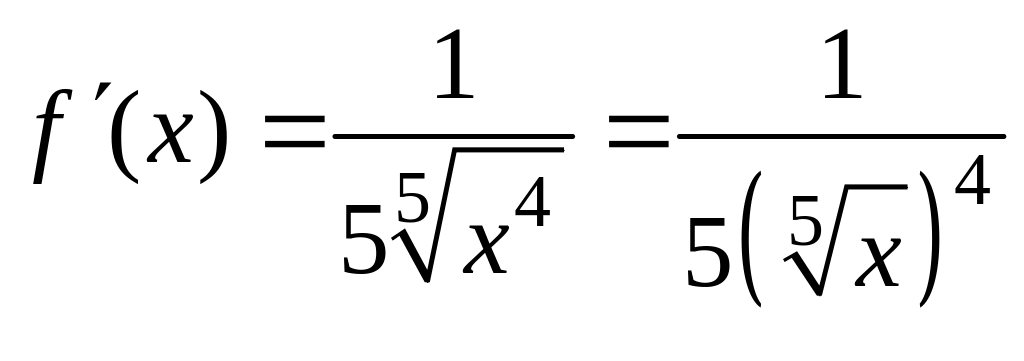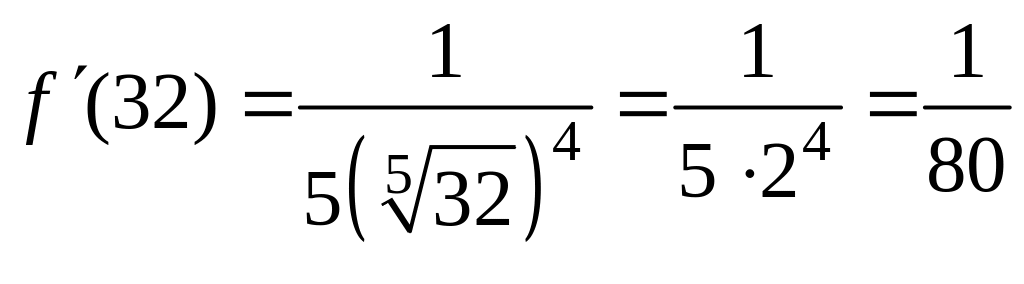Находим значение функции в точке :

.

Тогда

.



Дифференциалы высших порядков

Пусть дифференцируемая функция, а ее аргумент x – независимая переменная. Ее первый дифференциал есть также функция x. Можно найти дифференциал этой функции.

Дифференциалом второго порядка называется дифференциал от первого дифференциала, т.е.

.

Найдем выражение второго дифференциала функции . Так как не зависит от x, то при дифференцировании считаем постоянным:

.

Таким образом, получаем

. (16.13.)

Равенство (16.13.) есть формула, по которой находится дифференциал второго порядка функции , если x – независимая переменная.

Аналогично определяется и находится дифференциал третьего порядка:

.

И, вообще, дифференциал n-го порядка есть дифференциал от дифференциала (n1)-го порядка: .

Отсюда находим, что 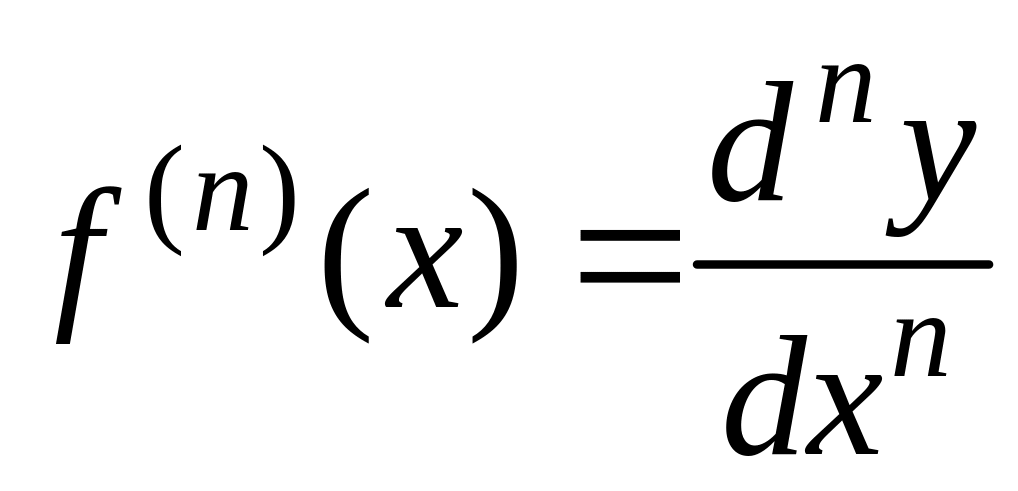. В частности, при соответственно получаем:

, , .

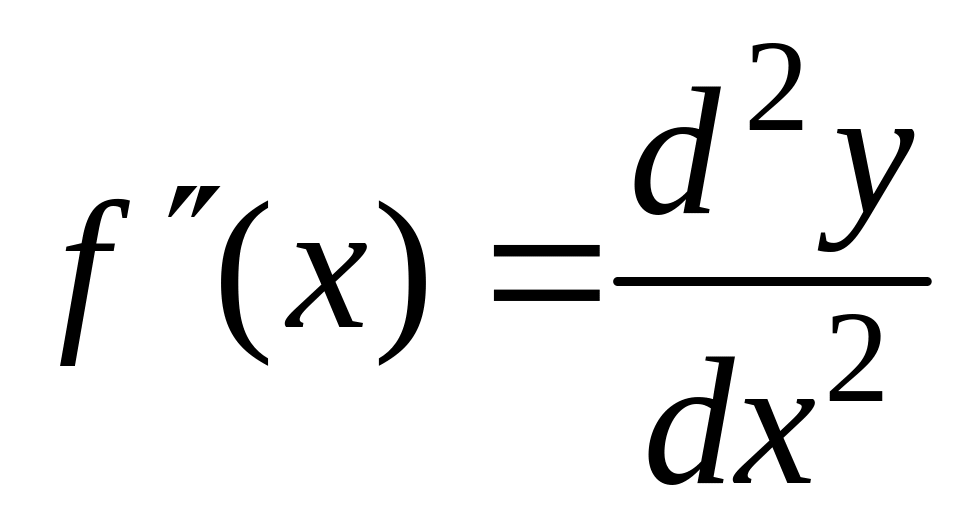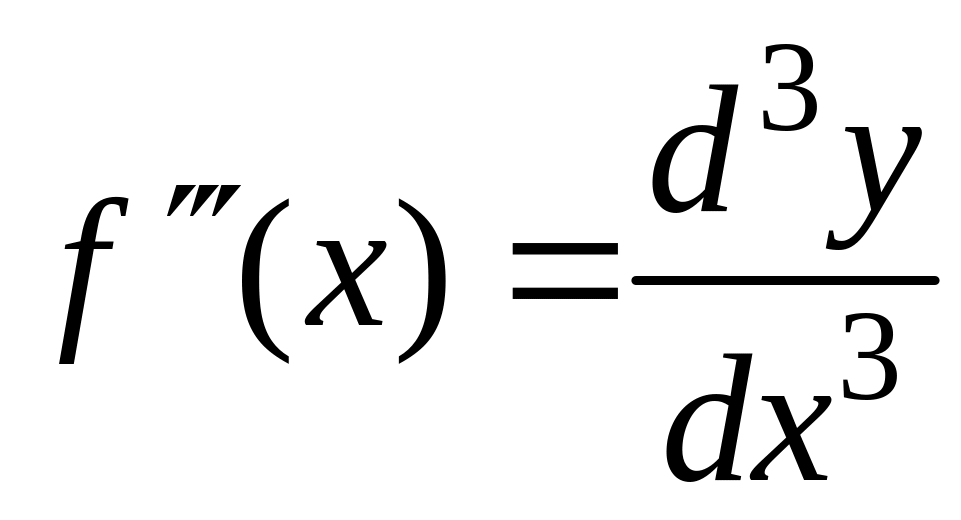т.е. производную функции можно рассматривать как отношение ее дифференциала соответствующего порядка к соответствующей степени дифференциала независимой переменной.

Отметим, что все приведенные выше формулы справедливы только, если x – независимая переменная. Если же функцию , где x есть функция от какой-то другой независимой переменной, то дифференциалы второго и выше порядков не обладают свойством инвариантности формы и вычисляются по другим формулам. Покажем это на примере дифференциала второго порядка.

Используя формулу дифференциала произведения ( ), полу-чаем:

,

т.е.

. (16.14.)

Сравнивая формулы (15.13.) и (15.14.), убеждаемся, что в случае сложной функции формула дифференциала второго порядка изменяется: появляется второе слагаемое .

Ясно, что если x – независимая переменная, то

и формула (16.14.) переходит в формулу (16.13.)

Пример 16.16. Найти , если , x – независимая переменная.

Решение. Находим последовательно и :

;

.

Тогда по формуле (16.13.) получаем

.



16.10. Основные теоремы дифференциального исчисления

Ниже мы увидим, что знание первой производной или производной более высокого порядка позволяет дать заключение о поведении функции. Но предварительно рассмотрим несколько основных теорем дифференциального исчисления.

Теорема 16.6. (Ферма) Пусть функция определена на интервале и во внутренней точке этого интервала принимает наибольшее или наимень-шее значение. Если существует конечная производная , то .

Доказательство. Пусть в точке принимает наибольшее значение, т.е. для . По определению производной

.

Этот предел не зависит от того, приближается x к слева или справа.

Разность , следовательно, при

,

а при

.

Переходим к пределу:

, .

Так как по условию существует, то односторонние производные равны и .



В доказательстве теоремы существенно, что - внутренняя точка интервала , так как мы рассматриваем точки справа и слева от . Если совпадает с концом промежутка, то производная может быть и не равна нулю. Например, функция на отрезке , а не на интервале , наибольшее значение достигает при . Однако . Тогда .

Теорема 16.7. (Ролля) Пусть задана функция и пусть она:

1) определена и непрерывна на ;

2) дифференцируема на интервале ;

3) имеет равные значения на концах отрезка, т.е. .

Тогда найдется хотя бы одна точка , что .

Доказательство. Пусть непрерывна на , следовательно, достигает наибольшего M и наименьшего m значений, т.е. . Рассмотрим два случая.

1. . Тогда , , , и любую точка из можно принять за c.

2. . Так как , то M и m не достигаются оба на концах отрезка, т.е. хотя бы одно достигается в точке . А по теореме Ферма .



Все условия теоремы Роля существенны. Если хотя бы одно из них не выполняется, то теорема тоже не будет выполняться. Например, для функции на отрезке условия 1 и 3 выполняются. На отрезке функция определена и непрерывна (первое условие), (третье условие). Но в точке функция не дифференцируема. Значит, теорема Ролля не выполняется.

Теорема 16.8. (Коши) Пусть заданы функции и и пусть:

1) они обе определены и непрерывны на ;

2) существуют и на ;

3) на .

Тогда найдется такая точка , что выполняется равенство

.

Доказательство. Очевидно, что . Так как если бы , функция удовлетворяла бы теореме Ролля и нашлась бы точка c между a и b, такая, что , а это противоречит условию на .

Введем вспомогательную функцию

.

Она удовлетворяет условиям теоремы Ролля. Действительно,

1) определена и непрерывна на ;

2) существует на ;

3) .

Следовательно, существует точка , такая, что . Действитель-но,

или

,

т.е.

.



Теорема 16.9. (Лагранжа) Пусть заданы функции и пусть она:

1) определены и непрерывны на ;

2) имеет конечную производную на .

Тогда найдется такая точка , что выполняется равенство

.

Доказательство. Теорему Лагранжа можно рассматривать как частный случай теоремы Коши. Действительно, положив , находим .

Подставляя эти значения в формулу , получаем или .



Формулу еще называют формулой Лагранжа или формулой о конечном приращении: приращение дифференцируемой функции на отрезке равно приращению аргумента, умноженному на значение производной функции в некоторой внутренней точке этого отрезка.

Теоремы Ролля, Коши и Лагранжа называются теоремами о средних значениях. Это значит, что для каждого отрезка существует по крайней мере внутренняя точка (не обязательно в середине отрезка!), для которой эти теоремы выполняются.