16.5. Дифференцирование функций, заданных неявно
Функции, которые рассматривались выше,
были представлены в виде
,
т.е. переменная y
выражалась через переменную x.
Если функция задана уравнением
,
разрешенным относительно y,
то функция задана в явном виде (явная
функция). Например,
,
задает две функции
.
Во многих задачах приходиться сталкиваться
с ситуацией, когда переменную y
невозможно выразить через x.
Например,
.
В этих случаях функция записывается в
виде
,
и говорят, что она задана неявно.
Под неявным заданием функции понимают задание функции в виде уравнения , не разрешенного относительно y.
Чтобы найти производную функции, которая
задана уравнением
(задана неявно), достаточно
продифференцировать это уравнение по
x,
рассматривая при этом y
как функцию x,
и полученное затем уравнение разрешить
относительно
.
Производная неявной функции выражается через аргумент x и функцию y.
Пример 16.4. Найти производную функции, заданной неявно:
.
Решение. Дифференцируем обе части данного уравнения, считая y функцией от x. Получаем
;
;
Отсюда находим
.
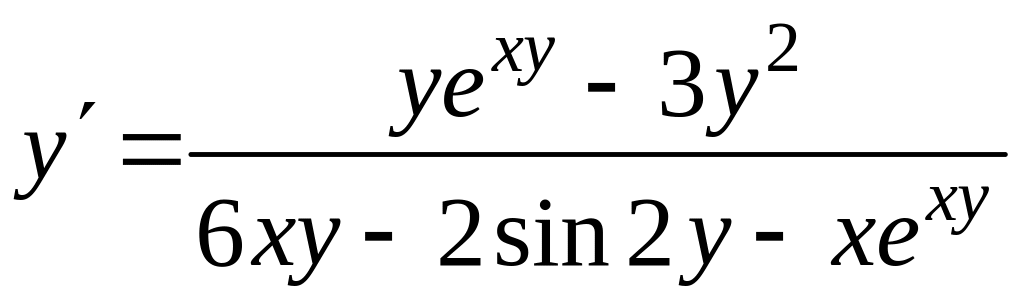Чтобы найти производную функции, заданную уравнением , где y – функция независимой переменной x, то можно воспользоваться следующей формулой:
.
Пример 16.4 (2). Найти производную функции, заданной неявно:
.
Решение. Находим
и
.
;
.
Затем находим
.
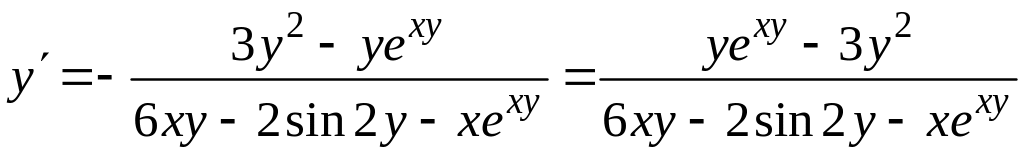Пример 16.5. Найти значение производной
функции в точке
,
если
.
Решение. Дифференцируем обе части данного уравнения, считая y функцией от x. Получаем
;
;
.
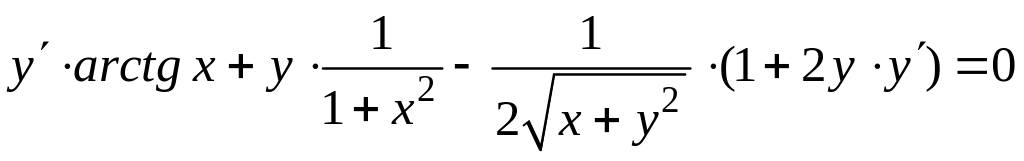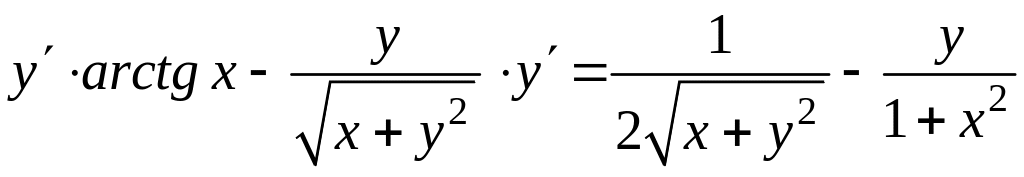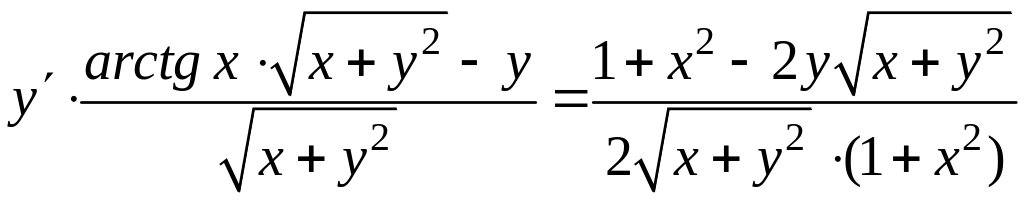Отсюда находим
.
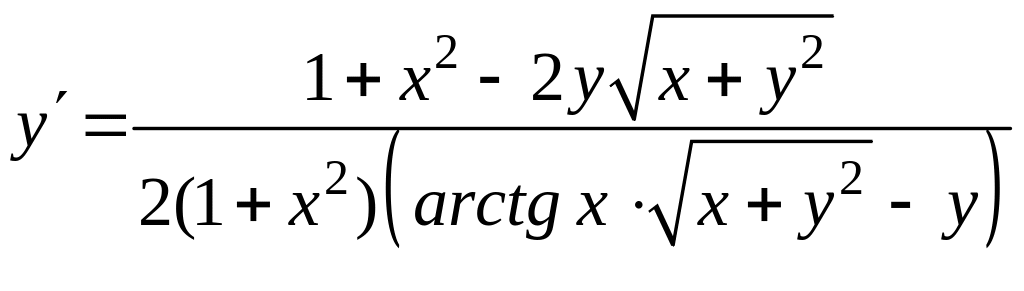Далее
.
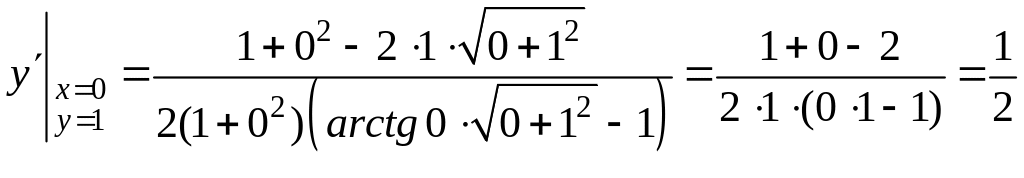16.6. Логарифмическое дифференцирование
В ряде случаев для нахождения производной целесообразно заданную функцию сначала прологарифмировать. А затем результат продифференцировать. Такую операцию называют логарифмическим дифференцированием.
Пусть
– некоторая функция. Прологарифмируем
обе части равенства, получаем
и вычисляем ее производную
.
Отсюда находим искомую производную:
.
Существуют функции, производные которых
находят лишь логарифмическим
дифференцированием. К их числу относится
так называемые степенно-показательная
функция
,
где
и
– заданные дифференцируемые функции
от x.
Найдем производную этой функции
;
;
,
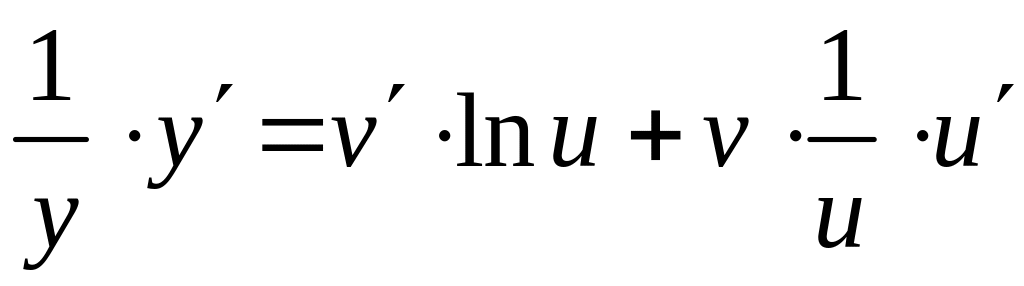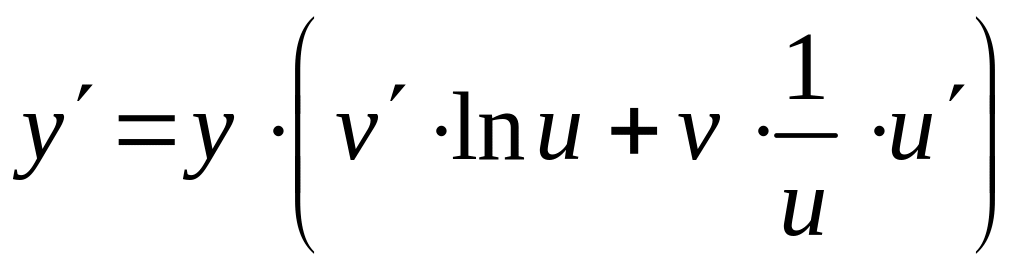т.е.
.
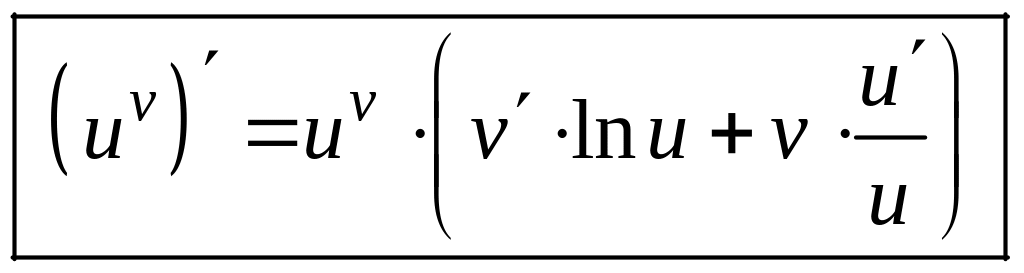(16.5.)
Запоминать эту формулу не стоит, гораздо полезней и проще усвоить схему вычисления логарифмической производной.
Пример 16.6. Найти производную функции:
.
Решение. Логарифмируем данную функцию, получаем
.
Дифференцируем обе части последнего равенства по x:
.
Отсюда
.
Пример 16.7. Найти производную функции:
.
Решение. Можно найти с помощью правил и формул дифференцирования. Од-нако такой способ слишком громоздкий. Применим логарифмическое дифференцирова-ние. Логарифмируем данную функцию, получаем
.
Дифференцируем обе части последнего равенства по x:
.
Выражаем , получаем:
.
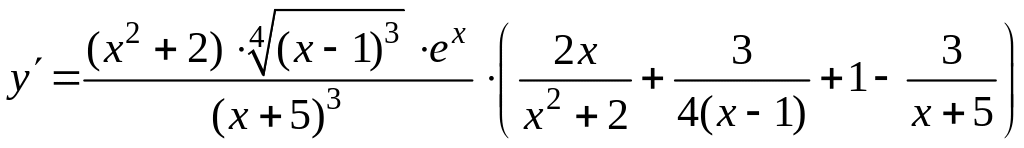