Обратимые и необратимые операции.

Вопрос о связи информации и необратимости - принципиальный. В идеально обратимом мире информация не может возникнуть, поскольку любой выбор не может быть запомнен (запоминание возможно лишь в диссипативных систе­мах). Поэтому необратимость в нашем мире играет существенную кон­структивную роль. Однако в фундаментальных законах классической и квантовой физики время обратимо, так что замена скоростей частиц на обратные эквивалентна повороту стрелы времени (т.е. замене ). Иными словами, в гамильтоновых системах явление необратимости не может иметь места.

Не останавливаясь на истории вопроса, отметим, что принципиально этот вопрос был решен Я.Г. Синаем при рассмотрении системы «бильярд Синая».

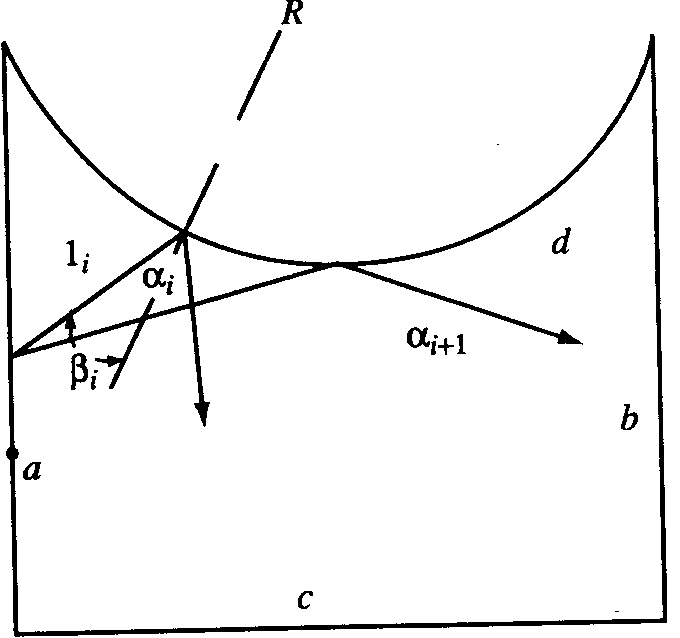
Рисунок 38

Отражение шаров от выпуклой стенки. Числа Ляпунова положительны. Неустойчивость как основа необратимости. Необратимость же нужна для того, чтобы система забыла свое прошлое состояние.

Возникает естественный вопрос: нельзя ли преодолеть квазиклассический термодинамический барьер и сделать компьютер термодинамически и логически обратимым? Оказывается, в определенном смысле можно!

Если в системе произошло стирание или потеря одного бита информации, то статистический вес состояния соответствующего элемента увеличится вдвое, а его энтропия возрастает на . При этом неизменно происходит рассеяние энергии и выделение тепла (в этом состоит так называемый принцип Ландауэра), соответственно уменьшается свободная энергия элемента F. Таким образом, логически необратимая операция – стирание бита информации, является также и термодинамически необратимой операцией. Чтобы сделать необратимый компьютер хотя бы логически обратимым, необходимо сохранять всю информацию, которая терялась бы в других случаях в процессе его работы.

В качестве одной из возможностей существенного уменьшения рассеиваемой мощности широко обсуждается использование процессов переключения, настолько медленных по сравнению с процессами релаксации внутри логического элемента, что в каждый момент времени он оказывается в квазиравновесном состоянии. При таком квазистатическим или адиабатическом процессе энтропия логического элемента практически не изменяется и, следовательно, не происходит рассеяние энергии ( ), а минимальная работа переключения совпадает с изменением внутренней энергии и может быть в принципе возвращена для полезного использования. Описанные соображения лежат в основе так называемой адиабатической динамической логики. Кроме адиабатических процессов для уменьшения рассеиваемой мощности были предложены схемы, позволяющие исключить в процессе переключения логического элемента протекание в нем токов.

Логический элемент осуществляет логически обратимую операцию, когда сигнал на его входе может быть однозначно определен по сигналу на выходе. В последнее время был предложен целый ряд другого рода обратимых логических устройств. При этом было показано, что при наличии шумов полностью избежать диссипации энергии все-таки оказывается невозможно. Отметим, однако, что логическая обратимость не обязательно требует бездиссипативных энергетических процессов. В оптимальном классическом компьютере с соответствующей обратимой логической архитектурой промежуточные результаты не должны стираться, переходы между состояниями при промежуточных операциях не должны быть слишком быстрыми, а надежность результатов не должна быть чрезмерной, для того, чтобы процесс переключения мог считаться и термодинамически обратимым. Необратимыми в компьютере будут лишь периферийные процессы ввода и вывода информации.

Фредкин и Тоффоли обратили внимание на аналогию логических операций в компьютерах с элементарными физическими процессами. Существенным их достижением было изобретение умозрительной механической модели идеально упругих “бильярдных шаров”, где каждый шар представляет собой неразрушаемый бит. Модель позволяет получать наглядную картину обратимых операций в так называемом механическом баллистическом компьютере. Многоэтапные вычисления реализуются в нем как иерархия субвычислительных обратимых операций, которые осуществляются в процессе упругих столкновений движущегося шара-бита с совокупностью “управляющих” шаров и неподвижных отражателей, изменяющих определенным образом направление его движения. Запущенный в устройство с определенной скоростью шар-бит в результате выходит из него в состоянии с той же энергией, но с новым направлением скорости, а само устройство обратимым образом возвращается в исходное состояние. Энергетическая и энтропийная цена бита информации в этом случае определяется только количеством стираемой на выходе и генерируемой на входе компьютера информации, поскольку промежуточного стирания не происходит. Такого рода схема была названа консервативной логикой. Однако на самом деле из-за неидеальности шаров и отражателей их движение будет быстро хаотизироваться и вычислительный процесс разрушится. Для сохранения необходимого порядка в движении шаров предлагалось ввести дополнительный периодически движущийся потенциал.

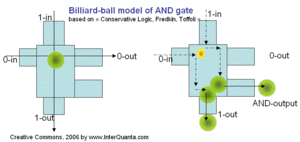
Рисунок 39