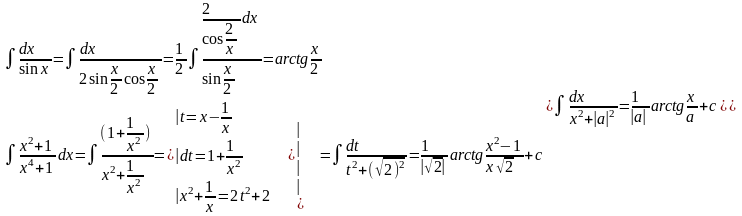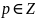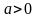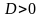Інтегрування дробово-раціональних функцій
Нехай
відношення двох многочленів
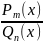є правильним дробом, тобто
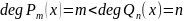,причому
;
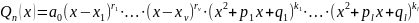
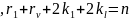Має місце:
;
Отже,
;
Інтегрування ірраціональних функцій
Розглянемо
інтеграли виду
,
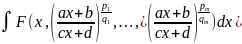де
;
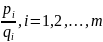- раціональні дроби.
Тоді
заміна:
,
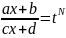де N – НСК
.
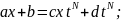
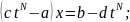
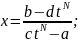
Отже,
,
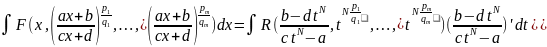де R(t) – раціональна функція.
Приклад.
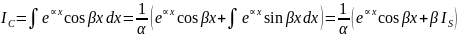
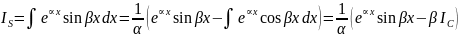
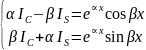
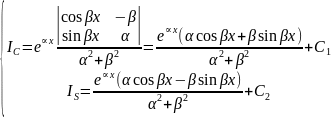
Метод підстановки або заміни змінної:
Якщо,
,
,
,
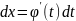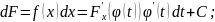
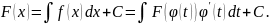
Метод інтегрування частинами:
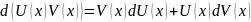
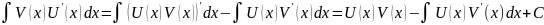
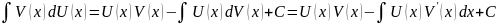
Таблиця інтегралів:
1)
2)
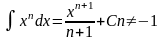
3)
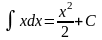
4)
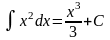
5)
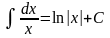
6)
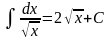
7)
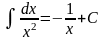
8)
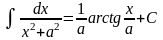
9)
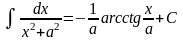
10)
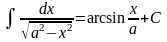
11)
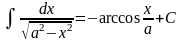
12)
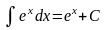
13)
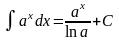
14)
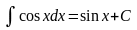
15)
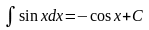
16)
17)
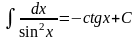
18)
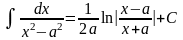
19)
Інтегрування дробово-раціональних функцій:
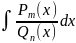
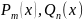-многочлени.
.
.
.
.
.
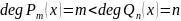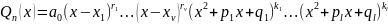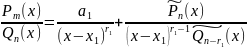Інтегрування ірраціональних функцій:
;
;
;
;
;
;
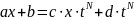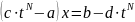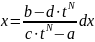Біноміальний диференціал:
;
;
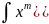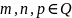Раціоналізувати можна, якщо:
Нехай
–
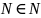спільний знаменник
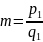і
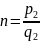
Заміна:
;
;
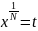
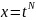
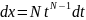
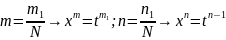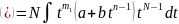Нехай
N
– знаменник
;
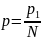Заміна:
;
;
;
;
;
;
;
;
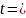
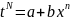
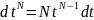
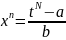
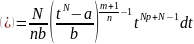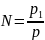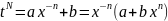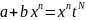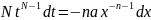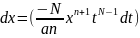Підстановки Ейлера
-
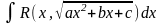
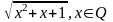
заміна Ейлера
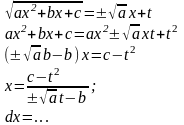
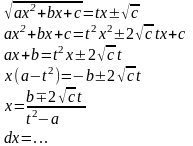
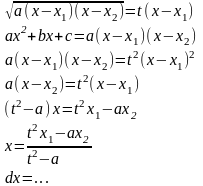
Отже, підінтегральна функція раціоналізується.
Інтегрування тригонометричних функцій
І
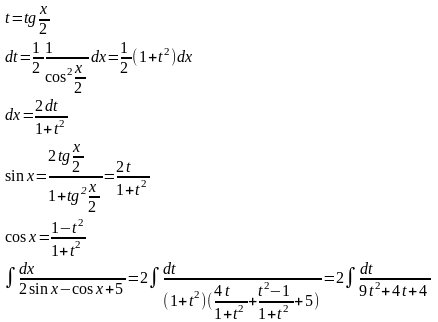
ІІ
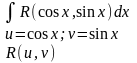
Нехай вона має наступні властивості:
1)
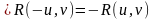
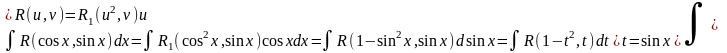2)
-
аналогічно
3)
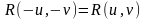
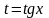
Визначені інтеграли
