Диференціали та похідні вищих порядків

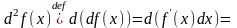
d x-?

Δx = dx – беремо який хочемо. Δx=dx

x^/-Δx x^/ x^/+Δx x^/-Δx x^/ x^/+Δx

Коли х – незалежний аргумент, то Δх – не залежить від цього х(від положення х), а це означає(з точки зору диф. числ.), що при d(Δx)=0(сприймаємо Δх за константу).

Δx=dx

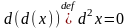
Тобто, коли х – незалежна змінна, то другий диференціал: d²x = 0

(похідна від похідної за означенням називається друга похідна)

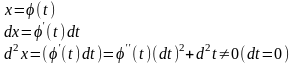
Висновок: форма другого диференціала не інваріантна відносно заміни змінної.

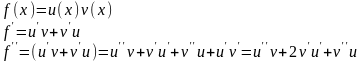
схоже на квадрат суми,тому далі з біноміальними коефіцієнтами.

Доведемо, що для n-ої похідної від добутку має місце узагальнення вищевказаних формул у нижче вказану:

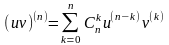- Формула Лейбніца.

Доводиться за мат. індукцією.

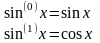
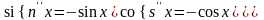
Степенево-показникові функції.

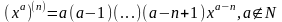
Коли а – натуральне, тоді

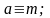
, при , якщо

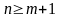
- логарифм натуральний.

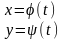
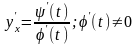
Визначення:

Формальний ряд

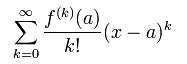
називається рядом Тейлора функції f в точці a.

Якщо a = 0, цей ряд называється рядом Макло́рена.

Формула Тейлора

Нехай задано многочлен

де а₀, а₁, ...,a_n - довільні дійсні числа, які називаються коефіцієнтами многочлена. Виразимо коефіцієнти даного многочлена через значення многочлена та його похідні.

З цією метою будемо послідовно диференціювати многочлен. Матимемо

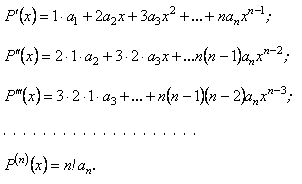
Підставляючи в ці рівності , дістаємо

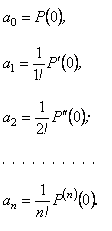
Тоді многочлен набуде вигляду

Може трапитися, що многочлен буде записаний за степенями різниці

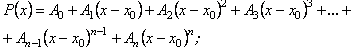
A₀,A₁,…,A_n –довільні числа

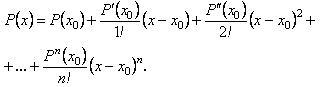
називають формулою Тейлора для многочлена.

Формула Тейлора для довільної функції

Візьмемо довільну функцію , яка в околі деякої точки і в самій точці має похідні до -го порядку включно.

Тоді для такої функції можна побудувати многочлен

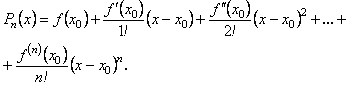
Цей многочлен називається многочленом Тейлора для функції

Розглянемо таку різницю:

Оскільки залежить від то й залежить від

Тоді

або

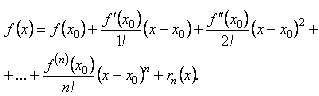
Данна формула називається формулою Тейлора для функції а функція - залишковим членом формули Тейлора.

Виразимо через похідну -го порядку від функції

Теорема.

Якщо в деякому околі, наприклад, на відрізку точки має неперервні похідні до -го порядку включно, то залишковий член у формулі Тейлора можна записати у вигляді

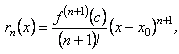
де

Тоді

і справедлива для будь-якого

Данна формула називається формулою Тейлора із залишковим членом виду Лагранжа. Якщо в цій формулі покласти , то матимемо так звану формулу Маклорена

Враховуючи вирази для диференціалів різних порядків функції можна записати цю формулу в диференціальній формі:

Формула Тейлора для функції двох змінних

Нехай функція має в околі точки неперервні частинні похідні до -го порядку включно. Формулу Тейлора зручно записати в диференціальній формі:

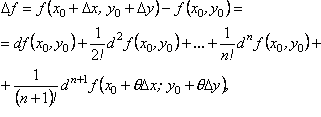
де

Аналогічний вигляд має формула Тейлора для функції більшого числа змінних.

Різні форми залишкового члена:

В формі Лагранжа:

В формі Коши:

Ряди Маклорена деяких функцій

Експонента:

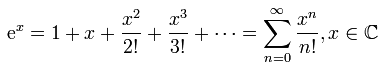
Натуральний логарифм:

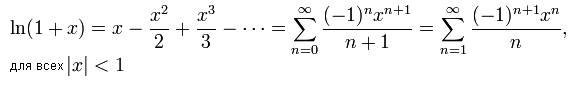
Біноміальний розподіл:

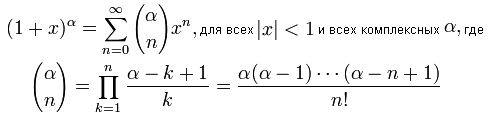
В частності:

Kвадратний корінь:

Геометричний ряд:

Тригонометричні функції: