Принцип математичної індукції

Нехай необхідно довести певний факт для 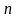елементів. Тоді:

1. вибирається будь-який елемент на цій множині ;

2. робимо припущення, що факт має місце для множини з 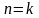, елементів;

3. на підставі даного припущення доводимо, що факт має місце на множині з елементів, з цього буде випливати, що факт вірний на всій множині з елементів.

Доведення:

Нехай для яких факт не вірний, . Тоді існує найменший елемент для котрого твердження не вірне, тоді для це твердження вірне. Але і для нього факт має місце, що суперечить припущенню про те, що твердження не вірне.

Означення

Множина 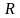дійсних чисел – множина на котрій визначені операції додавання і множення і відношення порядку ( ), що задовольняють аксіомам:

1) 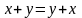(комутативність відносно додавання);

2) (асоціативність);

3) ;

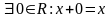4) ;

5) ;

6) ;

7) ;

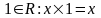8) (існування оберненого до елемента);

9) 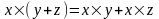(дистрибутивність);

10) (транзитивність);

11) ;

12) ;

13) ;

14) (аксіома повноти).

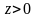Слід зазначити, що , якщо і , якщо .

Означення

Множина називається обмеженою зверху множиною, якщо , 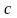називається верхньою межею . Множину верхніх меж позначають .

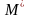Лема

Нехай обмежена зверху множина, – множина верхніх меж множини . Тоді такий, що 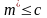, де .

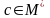Доведення:

З аксіоми повноти – верхня межа. .

Означення

Найменший елемент множини верхніх меж обмеженої зверху множини називається точною верхньою межею даної множини: .

Приклад

а) ;

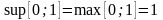б) .

Найбільшу нижня межа позначається .

Означення

Еквівалентне означення 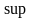: , якщо:

1) ;

2) .

Означення

необмежена зверху множина, якщо .

Лема (Архімеда)

Нехай 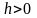. Тоді .

Доведення:

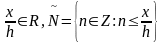– обмежена зверху, значить , з цього і випливає лема Архімеда.

Приклад :

Нехай .

Твердження

Нехай , тоді .

Доведення:

.

Твердження

Нехай , тоді .

Доведення:

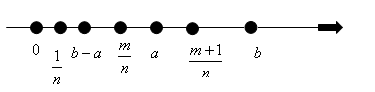
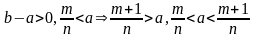, нам необхідно довести, що . Від протилежного:

, але , значить .

Означення

Потужність множини – це узагальнене поняття кількості елементів в цій множині. Якщо потужність множини 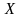і множини однакові, то цей факт записують наступним чином: . Множина, еквівалентна множині натуральних чисел, називається зліченною множиною. Про множини, рівнопотужні безлічі всіх дійсних чисел, кажуть, що вони мають потужність континууму, множина потужності континуум незліченна. Множина дійсних чисел – множина потужності континуум.

Принцип Коші-Кантора

Нехай є послідовність вкладених відрізків . Тоді , яке міститься в кожному відрізку . Якщо , тоді така точка єдина.

Доведення:

, доведемо, що для . Припустимо, що це не так: –- не вкладені, що суперечить умові, тобто . Доведемо, що така точка єдина від протилежного: , але константа не менша за довільне мале число.

Нехай 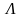деяка множина індексів 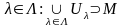. Нехай 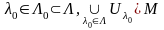, – підпокриття.

Лема (Гейне-Бореля-Лебега)

Нехай нескінченна множина індексів і інтервали 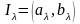утворюють покриття відрізка , . Тоді існує скінченне підпокриття цього відрізка ( ).

Доведення:

Підемо від протилежного, розіб’ємо відрізок на два рівних відрізка, потім виберемо з них той, що не покривається. Продовжимо цей процес і отримаємо вкладену систему відрізків. Тоді 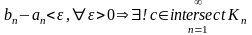. Ці відрізки не покриваються скінченною кількістю інтервалів, вони вкладені і всім їм належить одна єдина точка: . Але ми будували так, щоб не було скінченного покриття, значить ми прийшли до протиріччя.

Означення

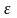-околом точки називається: . Виколотий -окіл: .

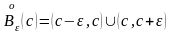Означення

називається відкритою, якщо .

Означення

Множина називається замкненою, якщо доповнення до неї є множина відкрита.

Твердження

Нехай – відкрита множина, тоді 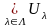– множина відкрита.

Доведення:

Беремо довільну точку з об’єднання, значить 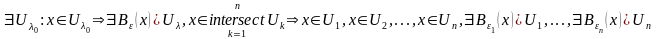. Тепер серед скінченної кількості виберемо найменший: .

Твердження

Нехай – замкнені, тоді – також замкнена.

Тотожності де Моргана:

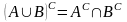
Твердження

Якщо – замкнені, тоді – замкнена.

Означення

Точка називається граничною точкою множини , якщо . Для множини , множина її граничних точок буде позначатися . Наприклад: .

Означення

називається обмеженою, якщо .

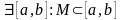Принцип Больцано-Вейєрштрасса

Нескінченна обмежена множина має хоча б одну граничну точку.

Доведення:

Підемо від супротивного: нехай немає жодної граничної точки, але оскільки множина обмежена, то 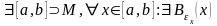, що він або не містить елементів з нашої множини, або містить скінченну їх кількість. Але , ми приходимо до протиріччя.

Границі і послідовності

Означення

Нехай кожному елементу з деякої множини ставиться у відповідність деякий елемент (лише один) з іншої множини 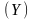, тоді кажуть, що задано функцію . При цьому 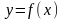. Множина значень функції: .

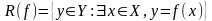Означення

Функція натурального аргумента називається послідовністю:

Означення.

.

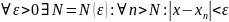Означення.

Якщо послідовність має границю – вона називається збіжною.

Послідовність яка прямує до нескінченності називається розбіжною.

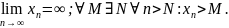
Збіжна послідовність обмежена, отже:

Арифметичні властивості границь:

Нехай

1. 

2. 

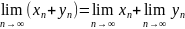
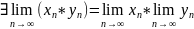
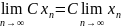3. Границя константи – константа.

4. (да, я не умею считать и после 2 у меня идет 4!!)

5. Нехай

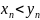
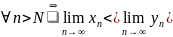
Теорема Вейерштрасса

Монотонна обмежена послідовність має границю.

 : + 

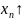
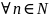
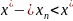Означення

Послідовність називається фундаментальною, коли

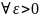N=N(),  n>N, p

Лема.

Фундаментальна послідовність обмежена.

Критерій Коші

Послідовність збіжна тоді і тільки тоді, коли вона фундаментальна.

Нехай

 N=N(),  n>N

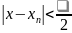
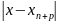< /2 <

Функція Метрика.

Нехай є множина Х – метричний простір, p(x,y) – деяка функція і виконуються умови

1. p(x,y)≥0, p(x,y)=0  х=у

2. p(x,y)= p(у,х)

3. p(x,z)≤ p(x,y)+ p(y,z) -- нерівність трикутника.

Множина Х, на якій введено Метрику називається метричним простором.

Якщо в метричному просторі довільна фундаментальна послідовність маю границю, то такий простір називається повним.

Якщо існує сума границь, то вона позначається сумою ряду.

= =

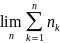Розглянемо 2 цікаві послідовності:

1. 

2. 

Доведемо, що

Отже – монотонно зростаюча

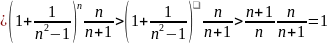
Отож , - монотонно спадаюча

За теоремою Вейерштрасса ці монотонні обмежені послідовності мають границю. Її позначають як

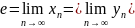e2.718

Цікаві границі при n :

=0

Теорема Тьоплеця:

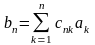
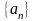
Теорема

Нехай послідовність має границю та елементи матриці С мають такі властивості:

1)

2)

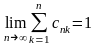
3)

Існує границя

Доведення: досить розглянути випадок

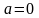
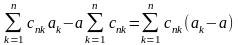
при великих k;

Теорема Штольца

Нехай послідовність , тоді якщо

Доведення:

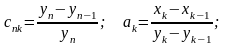
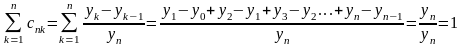
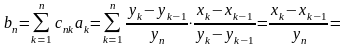
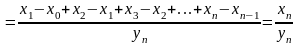
Приклади:

1)

____________________________________________

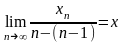
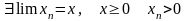
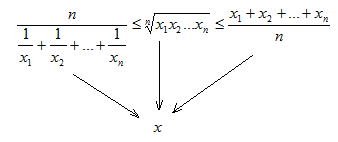
2)

Нехай

____________________________________________

____________________________________________

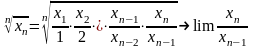
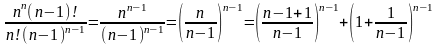
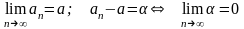
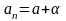
Частинні послідовності

x_nk - частинна послідовність

Якщо частинна границя послідовності {x_n}

Лема Больцано-Вейерштрасса:

Обмежена послідовність має хоча б одну частинну границю.

I Послідовність {x_n} приймає скінченну кількість значень

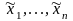
II Значеня:

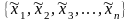
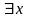– гранична точка

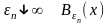
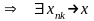
необмежена

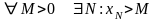
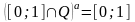
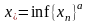
- буде граничною точкою

Діагональний метод Кантора:

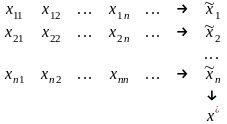
Означення:

Нехай {x_n} – обмежена послідовність, тоді її найбільша гранична точка називається верхньою границею і позначається:

Послідовність збіжна тоді і тільки тоді, коли її верхня і нижня границі співпадають.

Нехай

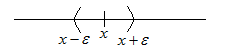
Оскільки всі граничні точки співпадають, то в будь-який окіл точки з якогось номера попадають всі члени послідовності, це означає, що є границею цієї послідовності.

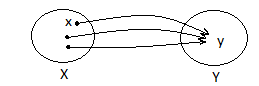
Функції та їхні границі

співставляється єдиний , тоді визначено функцію:

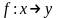
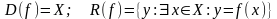
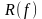- область значень

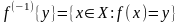
Якщо прообраз кожного елемента складається тільки з одного , то відображення називається ін’єкцією.

При ін'єкції 2 різних елементи переходять в 2 різних.

Якщо співпадає з , то -відображення на, а якщо не співпадають – відображення в. Якщо на все - то це сюр’єкція.

Відображення яке є сюр'єкцією і ін’єкцією одночасно називається бієкцією.

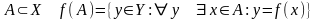
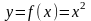
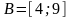
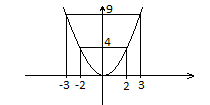
- образ множини А при відображенні

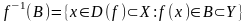
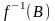- повний образ

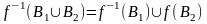
(підмножина дійсної осі) називається зв’язаною, якщо

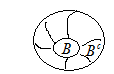
- доповнення

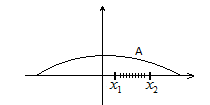
Означення: підмножина називається зв’язною, якщо для кожних 2 елементів цієї множини обов’язково відрізок між цими 2 елементами належить цій множині.

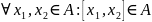
Границі функції.

1. Означення Коші

, якщо

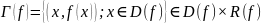
2. Означення Гейне.

якщо

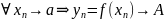
Арифметичні властивості.

1. 

2. 

3. 

4. 

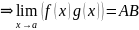
5. g(x)

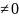
6. Нехай .

Зауваження:

7. 

Якщо .

8. 

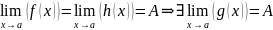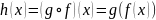
-- наскрізне відображення, композиція.

Теорема.

Нехай , .

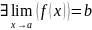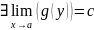
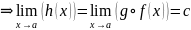Твердження.

Функція має границю тоді і тільки тоді, коли ліва і права границя співпадають.

Чудові границі.

1.

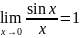
2.

3.

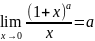
4.

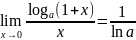
5.

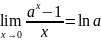
Ієрархія нескінченно малих границь.

Означення: Функція α називається нескінченно малою в околі точки , якщо .

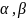– нескінченно малі в околі .

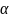називається нескінченно малою вищого степеня меншості відносно , якщо .

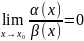Тоді кажуть, що 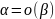( є о мале відносно ).

Наприклад: , в околі точки .

.

, – нескінченно малі і мають один порядок.

, .

Наприклад: , в околі точки .

.

Означення: Якщо тоді (еквівалентні).

Наприклад: .

Нехай і еквівалентні. Тоді

Доведення:

Означення: f =O(g) якщо така що .

.

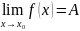в околі така, що . Тобто .

Коливання.

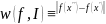
Наприклад: , , .

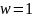Критерій Коші.

,

тобто .

Теорема Веєрштрасса про монотонні функції.

Нехай ,

– строго монотонна.

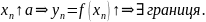
Неперервність функції

Означення: функцію f, визначену на деякому проміжку, називають неперервною в точці , якщо:

i

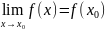
Розривна функція.

Означення: Нехай функція не є неперервною в точці , тоді вона називається розривною і точці .

,

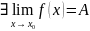
– точка розриву.

F – неперервна в точці .

,

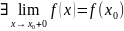
Якщо не співпадають хоча б два значення з трьох:

, , тоді

—точка розриву першого роду, функція матиме в цій точці стрибок.

Якщ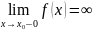о або 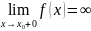тоді

—точка розриву другого роду.

Глобальні властивості неперервної функції

D(f)=[a,b]

Теорема Коші № 1

Нехай f неперервна функція на відрізку [a , b], f є Cº на [a,b]

І на кінцях цього проміжку вона приймає значення різних знаків f (a)·f(b)<0

Т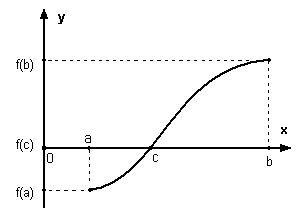 оді існує точка c є (a,b) така, що f(c)=0

Доведення:

Метод половинного ділення (a+b)/2=c₁

У випадку, коли f(c₁)=0 теорему доведено.

Розглянемо для (a+b)/2=c₁ , коли f(c₁)≠0

Спочатку з двох проміжків [a₁,c₁] чи [c₁,b₁] оберемо той , на якому функція має різні знаки. Ділимо його навпіл і повторюємо вибір проміжка, де функція приймає протилежні знаки на кінцях. Таким чином отримуємо вкладені проміжки:

I_n=[c'_n, c''_n] де c'_n-c''_n = (b-a)/2ⁿ

Наприклад: f(c'_n)≤0 і f(c''_n)≥0 (або навпаки), тоді

lim _n→∞ f(c'_n)≤0 , a lim f(c''_n)≥0

За теоремою Коші-Кантора про послідовність вкладених відрізків існує границя c , що одинакова для c'_n і c''_n .

Отже 0 ≤ f(с) ≥ 0 і f (c) = 0

Теорема Коші № 2

Нехай f є Cº [ a , b ]

Т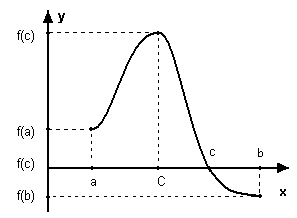 оді для будь-якого числа с , яке знаходиться між значеннями f(a) і f(b) знайдеться точка c є ( a , b) : f(c)=C .

Доведення:

Вважаємо, що f(a) < f(b) .

Розглянемо нову фукцію , яка є F(x) = f(x) - C . Оскільки F(a) < 0 , F (b) > 0 , то існує точка с , де F(c) = 0 , що і означає f(c) = C .

Теорема Веєрштраса № 1

Нехай f є Сº [a,b].

Тоді знайдеться така константа М > 0 , що |f(x)| ≤ M : (M₁ ≤ f(x) ≤ M₂).

З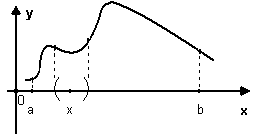 а локальними властивостями неперервної функції для кожної точки вибираємо інтервал x є [ a , b ] , для якого знайдеться такий окіл B_δ(x)(x) , що на ньому функція обмежена: M'_x < f(x) < M''_x .

Доведення:

Маємо нескінченне покриття відрізками.

За лемою Гейне –Бореля-Лебега про скінченне

покриття відрізка знайдеться скінченна кількість

B(x_k) k=1…n , що в об'єднанні покриють відрізок [a ,b].

Розглянемо М' = max М' x_k k=1…n;

M'' = max M'' x_k k=1…n;

Отже f(x) на проміжку x є [ a , b ] обмежена :

Inf f(x) ≥ M' ;

Sup f(x) ≤ M'' .

Теорема Веєрштраса № 2

Нехай f є Сº [ a , b ].

Тоді для x є [a , b ] знайдеться точка c є [ a , b ] : f(c) = sup f(x);

( в протилежному випадку f(c') = inf f(x) )

Доведення:

Візьмемо функцію g(x) (обмежена і неперервна):

М – f(x) > 0 ;

g(x) = 1 / (M-f(x)) ;

За означенням супремума:

Для будь-якого ε > 0 існує x' є [a , b ]: M – ε <f(x') <M;

Отже і для f(x) : M – ε <f(x) < M;

g(x) = 1/(M-f(x)) > 1/ε > k

Отримуємо протиріччя.

Рівномірно неперервна функція

Означення: функція f називається рівномірно непервною на області визначення, якщо для будь-якого ε>0 знайдеться δ = δ (ε) , що для пари будь- яких x' < x'' виконується: 0 < x'' - x' < δ ;

|f(x'') – f(x')| < ε .

Теорема Кантора

Якщо функція f неперевна на проміжку [ a , b ], то вона рівномірно непервна на ньому.

Доведення:

Нехай є окіл точки x є [a , b ] : B_δ(x). Тоді коливання функції в цій точці

ω ( f , B_δ(x) ) = sup ( f(x'') – f(x') ), де x' , x'' є B_δ(x).

Спершу доведемо , що функція f є неперевною.

Для будь-якого ε>0 знайдеться таке δ = δ( ε , x), що в околі B_δ(x): ω (f , B_δ(x)) .

Розглянемо відкриту множину:

V(x) = B_{δ(ε , x)/2}(x) ;

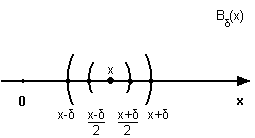
На множинному проміжку коливання точки менше, а значить ω ( f , V(x) ) <ε.

За лемою Гейне –Бореля-Лебега знайдеться скінченна кількість околів V(x₁)…V(x_n) таких, що в об'єднанні вони покриють відрізок [ a , b ].

Доведемо , що функція f рівномірно неперевна на проміжку [ a , b ].

Для цього нам потрібно довести, що які б ми дві точки з околу не взяли, для будь-яких x', x'' з V(x_k): |f(x'') – f(x')| < ε .

Візьмемо мінімальну амплітуду коливання: δ*= min{ δ(x_k)/2} k = 1…n ;

Беремо довільні дві точки x', x'' з [ a , b ] такі, що 0< x'' - x' < δ' з V(x_k).

Чи буде |f(x'') – f(x')| < ε ?

Розглянемо точку x' з V(x_k) , що напевне попадає в проміжок коливання. З'ясуємо чи попаде до околу точка x'' , а точніше чи буде | x''- x_k | < δ''.

Нехай у x' з V(x_k) є своя найменша амплітуда коливання 1/2· δ_x(x'_k) ≥ δ' :

| x''- x_k | = | x''- x'+ x'-x_k | ≤ | x''- x'| + | x'-x_k | ≤ δ' +1/2·δ_x(x'_k) ≤

≤1/2·δ_x(x'_k) + 1/2·δ_x(x'_k) = δ(x_k)

| x''- x_k | = δ(x_k) ;

Отже для будь-яких x', x'' B_δ(x_k) : |f(x'') – f(x')| < ε

Рівномірно неперервна функція на нескінченному проміжку

Якщо функція задовілняє умову Ліпшіца, то вона є рівномірно неперервною .

Доведення:

|f(x'') – f(x')| ≤ L| x'' - x' |< ε ;

| x'' - x' |< δ ;

δ = ε/L ;

L| x'' - x' | < L· ε/L = ε ;