1-2)
Программирование
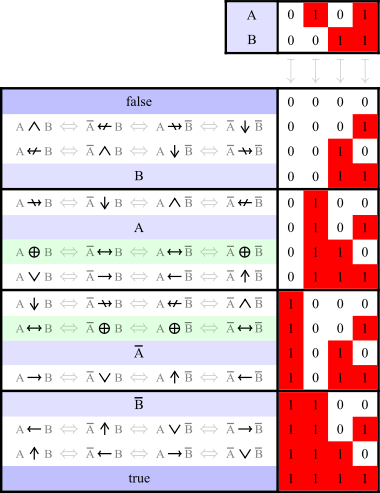
Логическая операция — в программировании операция над выражениями логического (булевского) типа, соответствующая некоторой операции над высказываниями в алгебре логики. Как и высказывания, логические выражения могут принимать одно из двух истинностных значений — «истинно» или «ложно». Логические операции служат для получения сложных логических выражений из более простых. В свою очередь, логические выражения обычно используются как условия для управления последовательностью выполнения программы.
В некоторых языках программирования (например в C) вместо логического типа или одновременно с ним используются числовые типы. В этом случае считается, что отличное от нуля значение соответствует логической истине, а ноль — логической лжи.
Значение отдельного бита также можно рассматривать как логическое, если считать, что 1 означает «истинно», а 0 — «ложно». Это позволяет применять логические операции к отдельным битам, к битовым векторам покомпонентно и к числам в двоичном представлении поразрядно. Такое одновременное применение логической операции к последовательности битов осуществляется с помощью побитовых логических операций. Побитовые логические операции используются для оперирования отдельными битами или группами битов, применяются для наложения битовых масок, выполнения различных арифметических вычислений.
В языках программирования
В следующей таблице для некоторых языков программирования приведены встроенные операторы и функции, реализующие логические операции.
Язык |
НЕ |
И |
ИЛИ |
Искл. ИЛИ |
Эквив. |
Не экв. |
Другие |
С++[2] |
! |
&& |
|| |
^ |
== |
!= |
|
Pascal[5] |
not |
and |
or |
xor |
= |
<> |
|
3)
Примеры и контрпримеры
Формулы в ДНФ:
Формулы не в ДНФ:
4)
Примеры и контрпримеры
Формулы в КНФ:
Формулы не в КНФ:
Но эти 3 формулы не в КНФ эквивалентны следующим формулам в КНФ:
5)
6)
Определение
Предика́т (n-местный,
или n-арный) —
это функция с
множеством значений 
(или
«ложь» и «истина»), определённая на
множестве 
.
Таким образом, каждый набор элементов
множества M характеризуется
либо как «истинный», либо как «ложный».
Предикат можно связать с математическим отношением: если (m1,m2,...,mn) принадлежит отношению, то предикат будет возвращать на ней 1. В частности, одноместный предикат определяет отношение принадлежности некоторому множеству.
Предикат — один из элементов логики первого и высших порядков. Начиная с логики второго порядка, в формулах можно ставить кванторы по предикатам.
Предикат называют тождественно-истинным и пишут:
если на любом наборе аргументов он принимает значение 1.
Предикат называют тождественно-ложным и пишут:
если на любом наборе аргументов он принимает значение 0.
Предикат называют выполнимым, если хотя бы на одном наборе аргументов он принимает значение 1.
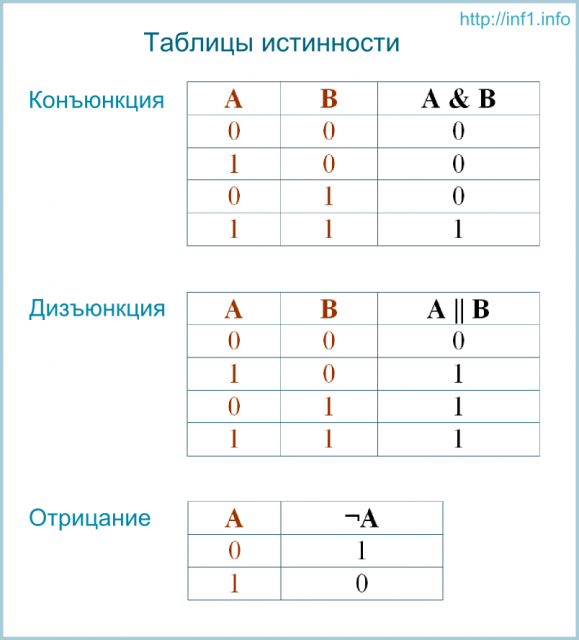
Так как предикаты принимают только два значения, то к ним применимы все операции булевой алгебры, например: отрицание, импликация, конъюнкция, дизъюнкция и т. д