20. Арифметические операции

Основное предназначение арифметических операций - выполнять определенные арифметические действия над числовыми данными: складывать, вычитать, умножать, делить и т. д. Это означает, что для арифметических операций все операнды вычисляются в числовом скалярном контексте. При этом строки, содержащие правильные числовые литералы, автоматически будут преобразованы в числовые значения: если строка не содержит правильного числового литерала, то интерпретатор попытается выделить из нее число, начиная с левого символа, и использовать его в качестве операнда; если не удается выделить правильный числовой литерал, то строковый операнд принимает нулевое значение.

Операции выполнения основных арифметических действий являются бинарными, так как для их выполнения требуется два операнда. Все, сказанное о преобразовании строк в числа, относится именно к таким операциям.

В языке определены также унарные арифметические операции: унарный плюс (+) и минус (-), а также операции автоматического увеличения (++) и уменьшения (--) значения операнда на единицу. Для операндов таких операций создается скалярный контекст, но результаты их выполнения для числовых и скалярных величин определяются совершенно разными алгоритмами.

Операции сравнения (операции отношения)

Применяются для сравнения (сопоставления) числовой или символьной информации. Результатом выполнения операций является либо истина (true), либо ложь (false). Перечислим эти операции:

<    — меньше;

<=   — меньше или равно;

==   — проверка на равенство (пишется два знака «равно» без пробелов);

!=   — проверка на неравенство;

>    — больше;

>=   — больше или равно.

Приоритет этих операций ниже, чем у арифметических операций. Пример использования:

A+B>=C

Проверяем: сумма A и B больше С? Если «да», то ответом будет true, если «нет», то false.

В использовании операций сравнения нет ничего сложного. Но следует обратить внимание на одно обстоятельство.

Вещественные числа в памяти хранятся приближенно, при работе с ними в ходе выполнения арифметических операций могут накапливаться погрешности, поэтомуне рекомендуется выполнять проверку на равенство или на неравенство для вещественных чисел, т.к. результат может быть непредсказуем. А если очень надо? Что делать?Поступаем просто. Если для вещественных чисел надо выполнить проверку на равенство (типа A==B), то заменяем её на проверку на неравенство вида

|A-B|<=ε,

где ε — некая малая положительная величина эпсилон.

В терминах языка C++ это будет выглядеть так

fabs(A-B)<=eps

Вот и всё решение проблемы. Единственно, не забудьте предварительно задать значение для эпсилон.

Логические операции

Чаще всего используются следующие логические операции:

• инверсия (отрицание, логическое не),

• конъюнкция (логическое и),

• дизъюнкция (логическое или),

• импликация (следование),

• эквивалентность (тождество).

Рассмотрим каждую из них подробно. Для описания используем диаграммы Эйлера-Венна и таблицы истинности.

Логическая операция/ соответствие в русском языке	Обозначение	Диаграмма Эйлера-Венна	Таблица  истинности
инверсия (отрицание, логическое "НЕ")/ "...не...", "неверно, что..."	¬		A	¬A
			0	1
			1	0
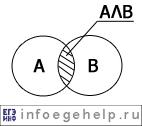
конъюнкция (логическое "И")/ "...и..."	Λ, &		A	B	AΛB
			0	0	0
			0	1	0
			1	0	0
			1	1	1
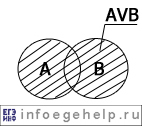
дизъюнкция (логическое "ИЛИ") "...или...", "...либо..."	V		A	B	AVB
			0	0	0
			0	1	1
			1	0	1
			1	1	1
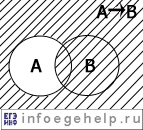
импликация (следование)/ "если...,то...", "когда..., тогда..."	→		A	B	A→B
			0	0	1
			0	1	1
			1	0	0
			1	1	1
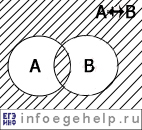
эквивалентность (тождество) "тогда и только тогда, когда"	↔, ≡		A	B	A↔B
			0	0	1
			0	1	0
			1	0	0
			1	1	1

Основные логические операции: инверсия, конъюнкция, дизъюнкция. 

Остальные логические операции можно выразить через них:

A→B=¬AVB;

A↔B=(AΛB)V(¬AΛ¬B).

Порядок выполнения логических операций в выражении (от наибольшего приоритета к наименьшему):

инверсия, конъюнкция, дизъюнкция, импликация, эквивалентность.

Пример:

AV¬BΛC→D↔E.

Порядок выполнения:

1. ¬B

2. (¬B)ΛC

3. AV((¬B)ΛC)

4. (AV((¬B)ΛC))→D

5. ((AV((¬B)ΛC))→D)↔E