§ 12. Дифференцирование неявно заданных функций.
ПРИМЕР.
(1) -
эллипс на
плоскости OXY.
y
-a 0 a x
,
такие, что
удовлетворяют
уравнению (1).
Таким образом, (1) определяет функцию y=f(x) (в данном случае двузначную). Такие функции называются неявно заданными. Примером неявно заданной функции двух переменных может служить функция, определенная уравнением конуса:
В общем случае:
а)
.
б)
.
в)
.
df.1
Пусть
и
.Уравнение
(2)
разрешимо в окрестности
если
существует функция
с
областью определения
и областью значений
,
что
.
Следует иметь ввиду, что в определении 1:
df.2
Пусть уравнение F(x,y)=0,
разрешимо в окрестности
тогда
уравнение (2)
определяет неявную функцию
в окрестности
.
В общем случае неявная функция многозначная.
Если для (2) существует единственное решение, то (2) – однозначно разрешимо; и (2) определяет однозначную функцию.
Т.к. рассматриваются только однозначные функции, то далее термин «однозначная» опускается.
Th.1 (Достаточное условие существования и непрерывности неявно заданной функции F(x,y)=0)
1.
.
2.
,
где
-это
окрестность представляет собой
прямоугольник, в котором находится
точка
.
3.
-
строго монотонна на
.
Тогда
определяет однозначную
функцию с областью значений
,
причем
.
(Б/Д).
Г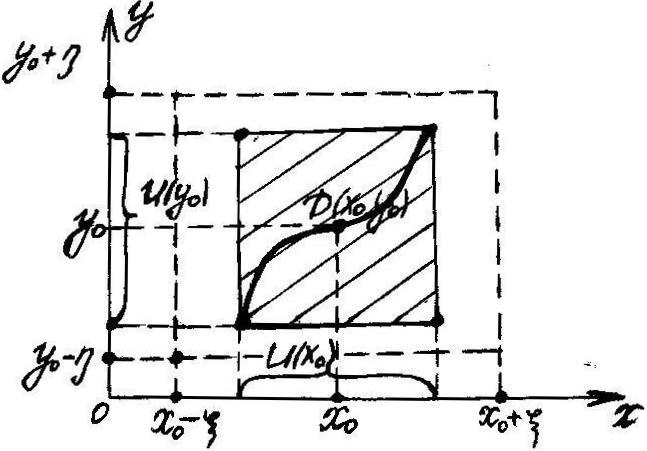
еометрический
смысл
Кривая, заданная уравнением F(x,y)=0 в прямоугольнике D представляет собой проходящий через точку график однозначной, непрерывной и непрерывно-дифференцируемой функции y=f(x).
Th.2 (Достаточное условие существования и непрерывности неявных функций многих переменных)
Пусть:
1.
.
2.
.
3.
.
Тогда,
,
что уравнение
=0
определяет
однозначную
непрерывную в
функцию:
=
,
причем
.
(Б/Д).
Th.3 (Достаточное условие существования частных производных неявной функции)
Пусть:
1. .
2.
3.
.
Тогда, существует
неявная функция
,
.
(4)
Доказательство:
Существует непрерывная в окрестности функция
из теоремы 2, т.к.
,
то по достаточному условию дифференцируемости
в точке F
– дифференцируема в
.
;
.
Пусть y=f(x),
,
т.к. F(x,f(x))=0,
.
Положим
при
(*)
при
.
в силу непрерывности
.
Найдем предел (*)
при
(4).
Непрерывность
из теоремы о непрерывности сложной
функции и арифметических действий.
СЛЕДСТВИЕ.
Пусть:
1.
.
2.
.
3.
.
Тогда, 1)
неявная
функция
такая, что
2)
,
причем
(5)
(5)
следует из теоремы 3 при
.
ЗАМЕЧАНИЕ 1.
При решении
практических примеров обычно дифференцируют
уравнение
=0
, как сложную функцию. Затем решают
уравнение относительно
.
ЗАМЕЧАНИЕ 2.
При отыскании второй производной (и т.д.) дифференцируем исходное уравнение дважды (и т.д.).
ЗАМЕЧАНИЕ 3.
Можно показать,
что в условиях теоремы 3 неявная функция
дифференцируема. Дифференциал
находят k-кратным
вычислением дифференциала от левой и
правой частей уравнения.
ПРИМЕР.
Найти
.
П
усть
Дифференцируем по «x»:
.
Неявные функции
могут задаваться системой уравнений.
Пусть
,
тогда
.
df.1
-
декартово произведение пространств
.
Р
ассмотрим
систему уравнений:
или
Введем важное определение:
df.2
Пусть
матрица:
При m=n:
- определитель
Якоби или Якобиан.
Th.4 Пусть:
1.
.
2.
.
3.
.
Тогда: 1) Система
(6) однозначно
разрешима в
и существуют неявные функции
,
причем
.
2)
.
(Б/Д).
П
ри
решении практических задач необходимо
непосредственно дифференцировать
каждое уравнение, а затем решать
соответствующую систему уравнений
относительно соответствующих производных
или дифференциалов.
Так например рассмотрим систему:
Тогда
И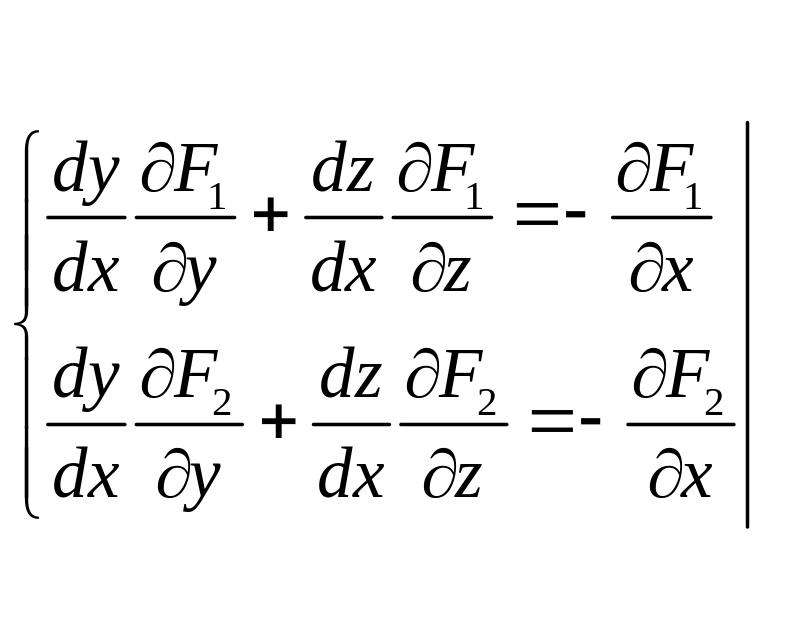
з
системы следует: первый раз
второй раз
Получим:
или
или
=
.
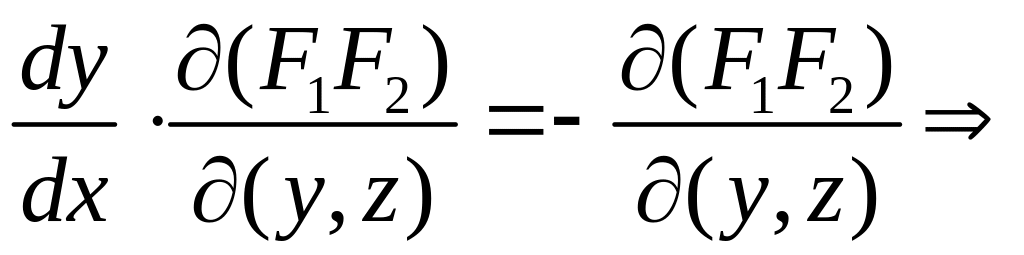
Аналогично находим:
.
Умножим и сложим уравнения:
.
ПРИМЕР.
Найти
.
Решение:
,
каждый раз складываем уравнения:
,
Ответ:
;
.