
- •Глава 7. Дифференциальное исчисление функций.
- •§ 1. Основные понятия. Пространство .
- •§ 2. Предел последовательности в .
- •§ 3. Функции на .
- •§ 4. Предел функции .
- •§ 5. Непрерывность функций многих переменных.
- •§ 6. Свойства непрерывных функций.
- •§ 7. Частные производные.
- •§ 8. Дииференцируемость функций многих переменных.
- •§ 9. Дифференцирование сложной функции.
- •§ 10. Частные производные и дифференциалы высших порядков.
- •§ 11. Градиент функции. Производная по напрвлению.
- •§ 12. Дифференцирование неявно заданных функций.
§ 8. Дииференцируемость функций многих переменных.
Пусть
![]() (1)
определена в некоторой окрестности
(1)
определена в некоторой окрестности
![]() ,
,
![]() .
.
df.1
Полным приращением функции f
в точке
,
соответствующим приращениям
![]() аргументов, называется выражение:
аргументов, называется выражение:
![]()
П ри
n=2
ри
n=2
y
![]()
![]() D
D
x
df.2
Функция
называется дифференцируемой в точке
![]() и ее полное приращение в этой точке
может быть представлено в виде:
и ее полное приращение в этой точке
может быть представлено в виде:
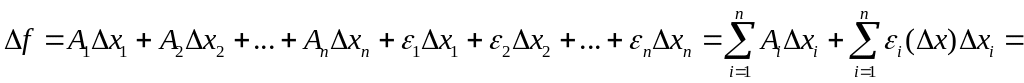
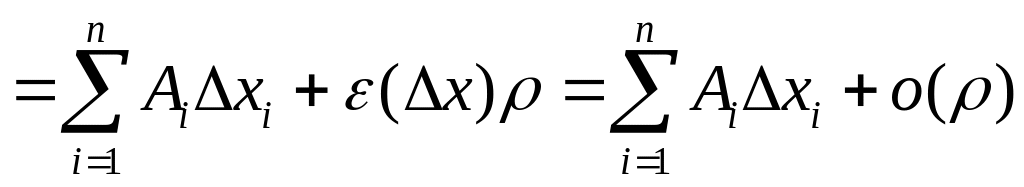 (2)
(2)
Где
![]() -
независящее от
-
независящее от
![]() числа, а
числа, а
![]() - бесконечно малое при
- бесконечно малое при
![]() функции,
.
функции,
.
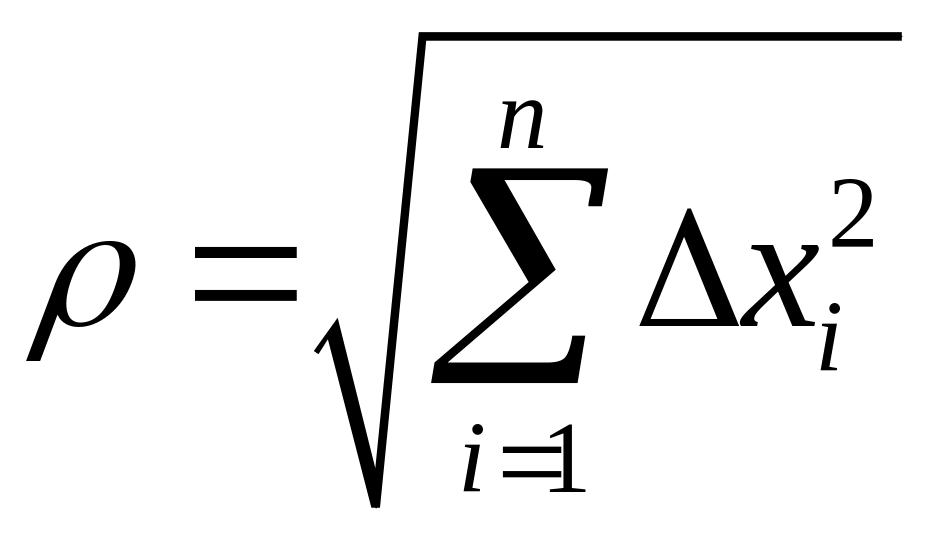 -
расстояние между точками
-
расстояние между точками
![]() и
.
и
.
Отметим, что запись
![]() (или
(или
![]() )
эквивалентна записи
)
эквивалентна записи
![]() при
при
![]() .
.
Условие (2) называется условием дифференцируемости функции в данной точке.
Если (векторная)
функция f
дифференцируема в точке
![]() ,
то будем писать
,
то будем писать
![]() если
если
![]() .
.
df.3
Пусть f
– дифференцируема в точке
.
Дифференциалом функции f
в точке
![]() главная
линейная относительно приращений
аргументов часть полного приращения f
в точке
.
главная
линейная относительно приращений
аргументов часть полного приращения f
в точке
.

Обозначение
![]() .
.
ЛЕММА.
Если
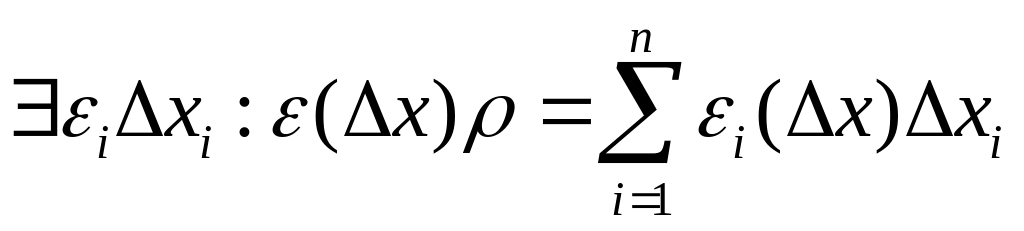 ,
где
,
где
![]()
![]() .
.
Доказательство:
Действительно,
при
![]() :
:
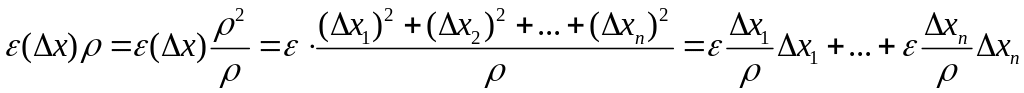 ,
,
Пусть
 ,
но
,
но

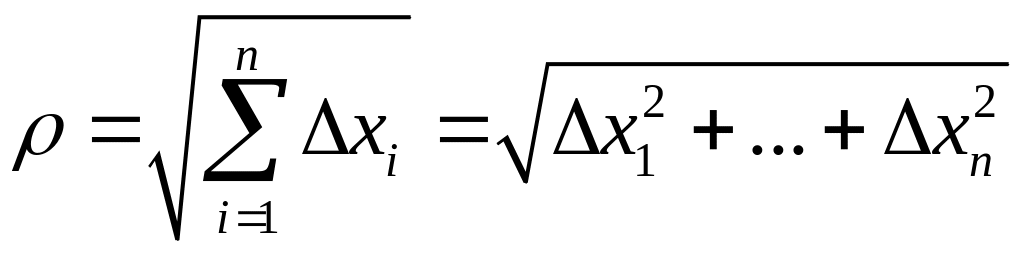 .
.
Th.1
Пусть f
дифференцируема в точке
,
тогда
![]() ,
или
,
или
![]() ,
тогда
,
тогда
![]()
![]() =
=
=![]() .
.
Доказательство:
Согласно определению
№3 и Лемме:
![]() ,
такая что:
,
такая что:
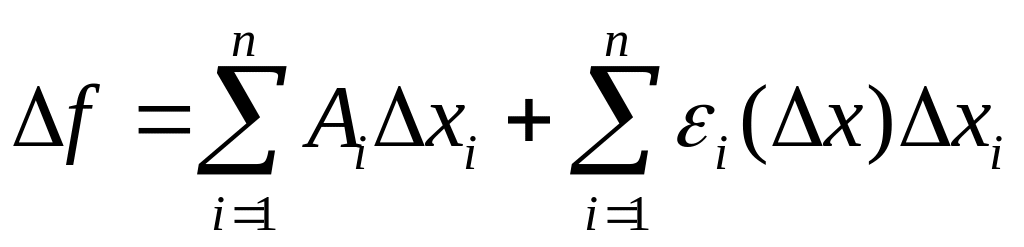 (2)
(2)
![]()
Причем (2)
справедливо
![]() ,
что
,
что
![]() .
Пусть
.
Пусть
![]() ,
отсюда при
,
отсюда при
![]() :
:
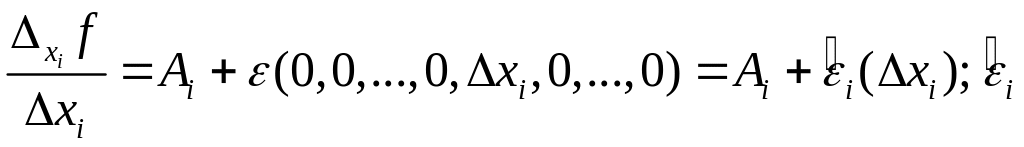 -
бесконечно
малое при
.
-
бесконечно
малое при
.
По свойству пределов
функции одного переменного (Необходимое
и достаточное условия существования
предела)
 (в обратную сторону неверно).
(в обратную сторону неверно).
СЛЕДСТВИЕ.
Пусть
![]() -
дифференцируема в точке
дифференциал
f
определяется
единственным образом формулой:
-
дифференцируема в точке
дифференциал
f
определяется
единственным образом формулой:

Единственность следует из единственности производных.
Th.2 (Необходимое условие дифференцируемости)
Пусть
-
дифференцируема в точке
f
–непрерывна
в точке
или
![]() .
.
Доказательство:
Т.к. f
– дифференцируема
в точке
,
то
и
 ;
;
![]() ,
т.к.
,
т.к.
![]()
 .
.
Предел правой
части =0 при
![]() f
непрерывна
в точке
f
непрерывна
в точке
![]() (в обратную сторону утверждение не имеет
смысла).
(в обратную сторону утверждение не имеет
смысла).
Th.3 (Достаточное условие дифференцируемости)
Пусть
![]() в
в
![]() и
и
![]() -
непрерывна в точке
-
непрерывна в точке
![]() - дифференцируема в точке
.
- дифференцируема в точке
.
Доказательство:
Проведем
доказательство для случая
![]() ,
т.е.
,
т.е.
![]() .
Найдем приращение:
.
Найдем приращение:
![]()
=![]() (при-
меним теорему Лагранжа)=
(при-
меним теорему Лагранжа)=![]()
(в силу непрерывности
![]() )=
)=![]()
= .
.
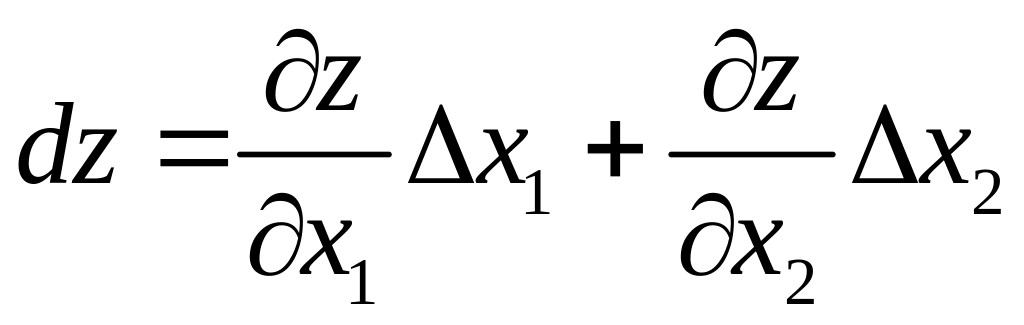 или
или
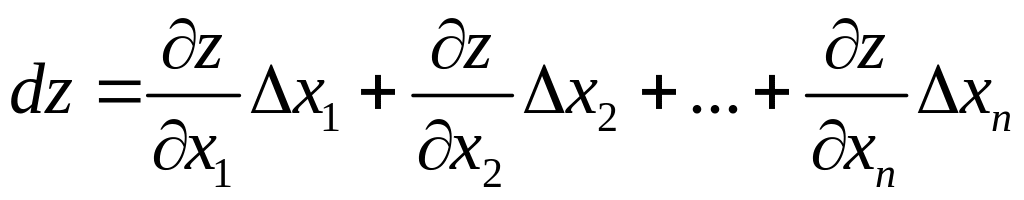 .
.
df.4 Функция, имеющая непрерывные частные производные на множестве G, называется непрерывно-дифференцируемой на G.
Обозначение:
![]() ,
то будем писать
.
,
то будем писать
.
§ 9. Дифференцирование сложной функции.
![]()
Рассмотрим функцию:
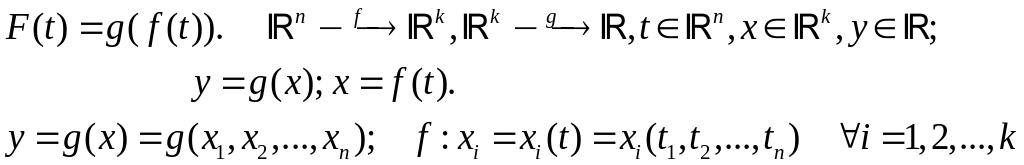
Th.1 Пусть :
g(x) определена в
 ,
функция f(t)
определена в
,
функция f(t)
определена в
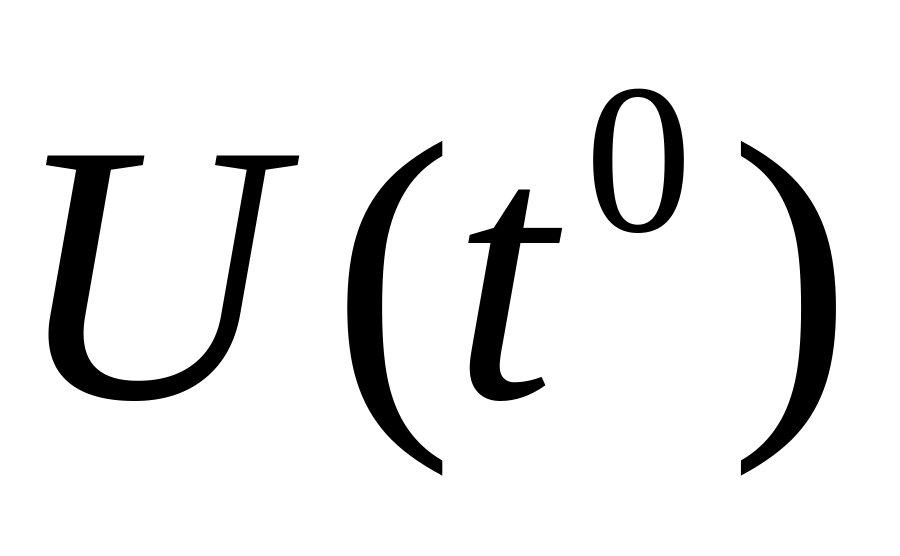 ,
где
,
где
 .
.g(x) дифференцируема в точке (т.е.
 ).
).
Тогда
![]() :
:
 (1)
(1)
Доказательство:
а) пусть n=1. g(x) дифференцируема в точке
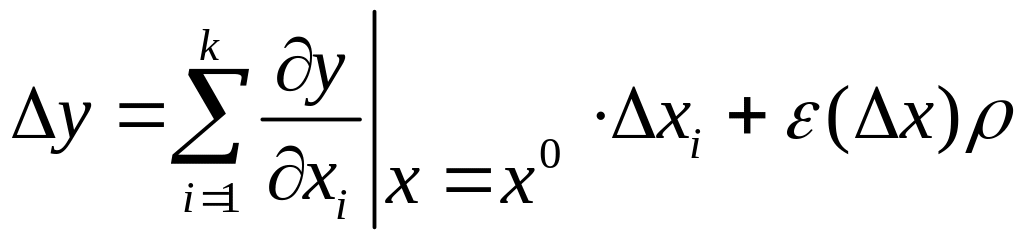 ,
,
 .
Причем
.
Причем
![]() .
.
Пусть
![]() при
при
![]() :
:
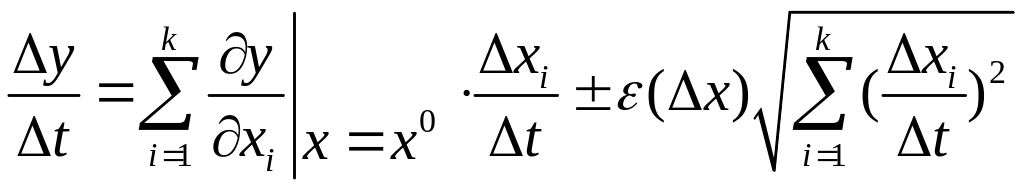 (*)
(*)
Т.к.
 непрерывна в точке
непрерывна в точке
![]() при
при
![]() .
Кроме того
.
Кроме того
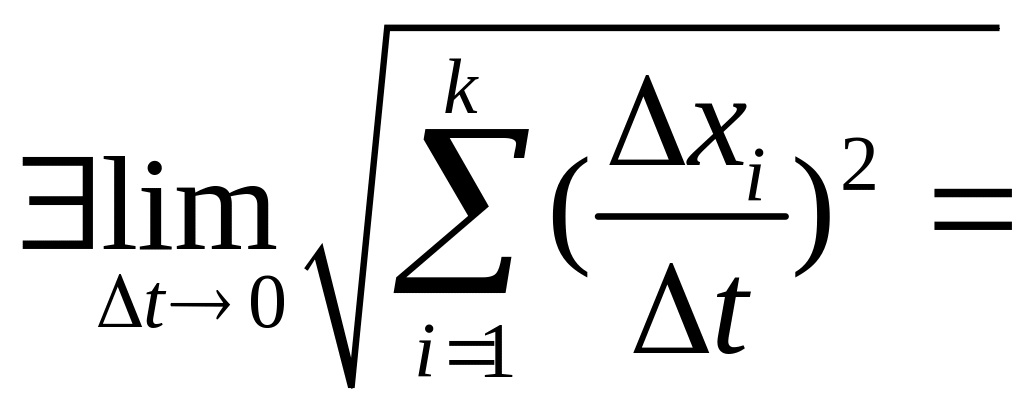
= переходим
к пределу в (*)
при
переходим
к пределу в (*)
при
![]() :
:

б) n>1.
Это частный случай пункта а), т.к.
рассматриваемая функция
![]() т.е.
имеем y=g(x).
т.е.
имеем y=g(x).
![]() ,
т.к.
,
т.к.
 ч. и т. д.
ч. и т. д.
Выпишем формулу (1) для всех частных случаев: n=1, k=2:
![]()
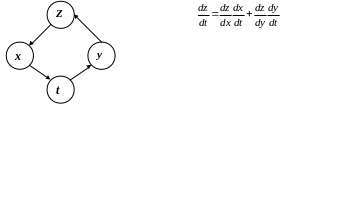
ПРИМЕР.
![]() .
.

![]()
n=2, k=2:
![]()
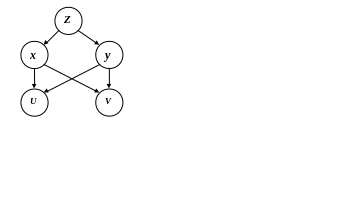

Пусть
![]() ,
где
,
где
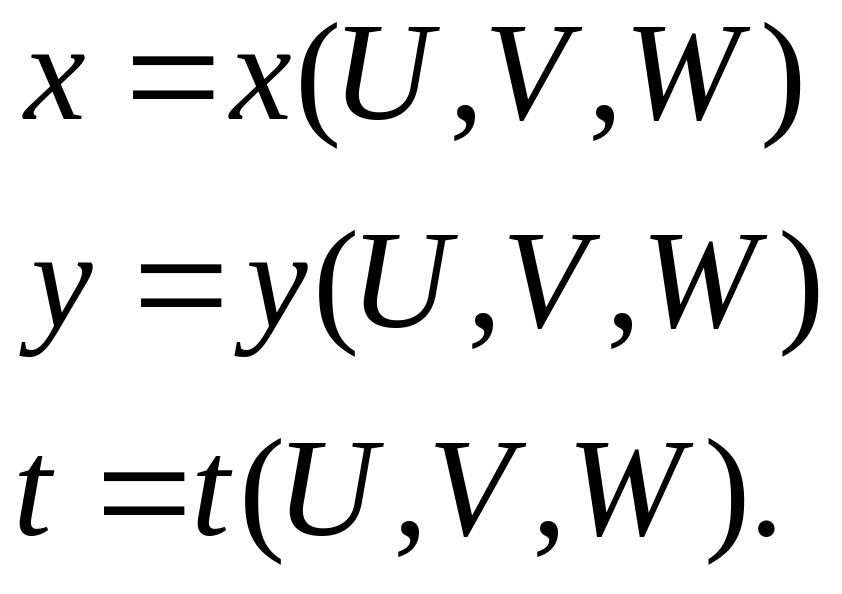


ПРИМЕР.
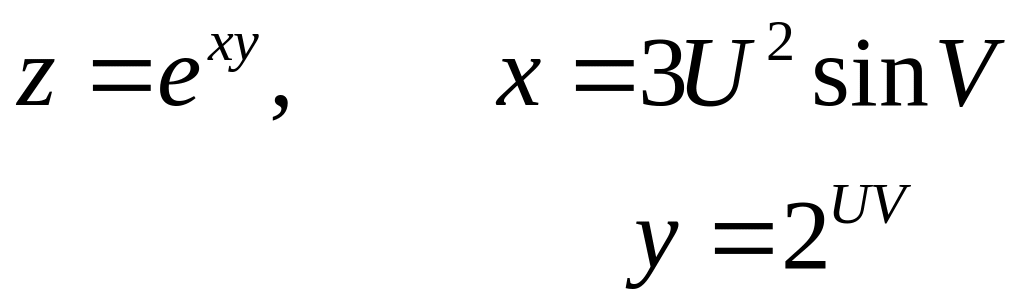

 .
.
df.1
Пусть
![]() ,
,
![]() и удовлетворяет
условиям Th.1
в точке
и удовлетворяет
условиям Th.1
в точке
![]() .
Тогда
.
Тогда
![]()
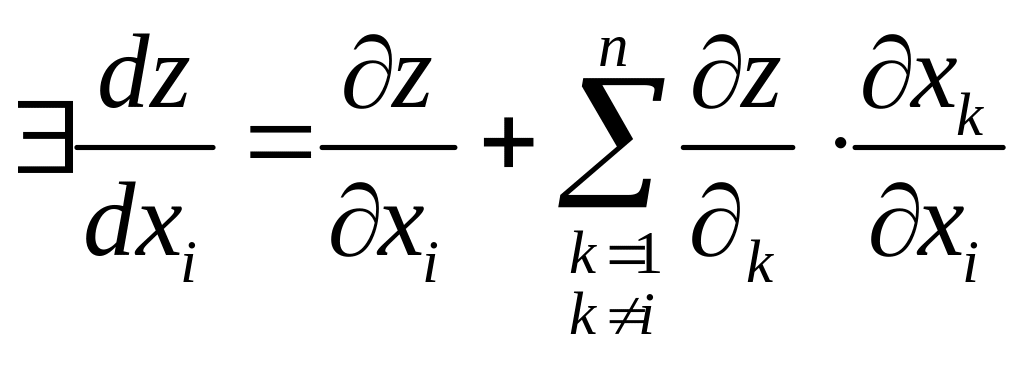 -
полная производная.
-
полная производная.
Доказательство
формулы следует из Th.1
при
![]() .
При
.
При
 .
.
Th.2 (Инвариантность формы записи первого дифференциала)
Пусть y=g(x)
– дифференцируема в точке
![]() -
дифференцируема в точке
-
дифференцируема в точке
Сложная функция y=g(x(t))=F(t) – дифференцируема в точке
 .
. (Б/Д).
(Б/Д).
ЗАМЕЧАНИЕ.
Пусть функция
f(x),
![]() дифференцируема во всех точках некоторого
открытого множества
дифференцируема во всех точках некоторого
открытого множества
![]() .
Тогда в каждой точке
.
Тогда в каждой точке
![]() можно вычислить дифференциал:
можно вычислить дифференциал:
 .
.
Он будет функцией
2n
переменных
![]() причем
при
причем
при
фиксированных
дифференциал есть линейная функция
![]() .
Правила дифференцирования такие же,
как и для функции одной переменной.
.
Правила дифференцирования такие же,
как и для функции одной переменной.
а)
![]()
б)
![]()
в)
![]() ,
если
,
если
![]() .
.
Докажем б).
Из Th о дифференцируемости сложной функции следует, что функция
U(x)V(x)
дифференцируема, если дифференцируемы
U(x)
и V(x).
Далее имеем:
 =
=
=![]() .
.
ПРИМЕР.
Найти дифференциал
функции
![]() .
.
Решение.
Пусть
![]() ,
тогда:
,
тогда:

