§ 6. Свойства непрерывных функций.

Для функций многих переменных (Ф. М. П.) справедливы основные свойства функций одной переменной, но при этом следует иметь ввиду, что многие свойства f(x) существенно зависели от области определения. Так в формулировках многих свойств существенным было то, что функция задавалась на сегменте.

I. Th.1 Пусть , тогда:

1. .

2. .

3. .

4. Если дополнительно , то

Доказательство:

Из определения непрерывности и теоремы о пределе функций этого вида.

II. Th.2 Если , где E – компакт , тогда она :

1. Ограничена на нем: .

2. Принимает свое наибольшее и наименьшее значение: т.е. , такие, что .

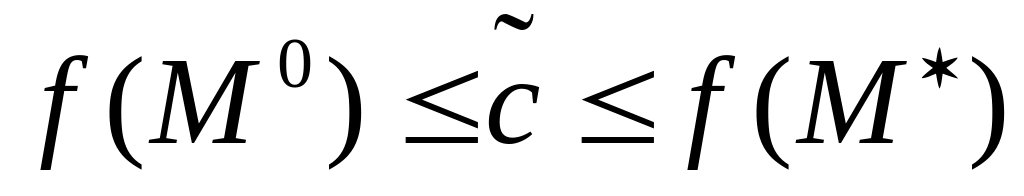
3. , таких, что , такая, что (принимает все промежуточные значения).

4. f в E – равномерно непрерывна, т.е. ,

Пусть - метрические пространства, .

df. Функция называется равномерно непрерывной на множестве E, если

)

Th.3 (Теорема Вейерштрасса)

Пусть - компакт, тогда f ограничена на E и достигает на E своей верхней и нижней граней (наибольшего и наименьшего значений), т.е. .

§ 7. Частные производные.

Пусть в некоторой (открытой) области D имеем функцию , возьмем точку . Примем y и z за постоянные значения и будем изменять x, тогда функция U будет функцией одной переменной (в окрестности точки ). Вычислим производную этой функции в точке . Придадим этому значению приращение , тогда функция получит приращение:

- это и есть частное приращение (по x).

По определению производной, она представляет собой предел:

- эта производная называется частной производной функции f(x,y,z) по x в точке .

В этом определении не все координаты равноправны, т.к. наперед фиксированы, а x меняется, стремясь к .

Частную производную обозначают одним из символов:

(круглым вместо прямого в обозначении частной производной предложил пользоваться Карл Густав Якоби (1804-1851))

.

Аналогично вводятся частные производные по .

df:

df:

Где - приращения функции соответственно по переменным .

Изложенные рассуждения для функции 3-х переменных остаются справедливыми и для функций любого числа переменных.

Рассмотрим функцию y=f(x), где или k=1.

Пусть f определена в некоторой окрестности точки .

df.1 Частным приращением в точке функции f по переменной называется , где .

Очевидно, если все переменные за исключение зафиксированы, то - есть функция одного переменного, т.е. .

df.2 Частной производной функции f по переменной в точке называется обычная производная функции f при всех фиксированных переменных кроме , т.е.:

, если этот предел существует. Очевидно, при n=1 это определение совпадает с определением обычной производной.

ПРИМЕР.

, т.е. имеем функцию двух переменных .

Из определения частных производных следует, что при их вычислении можно пользоваться всеми правилами вычисления обычных производных.

ПРИМЕР №1.

Решение:

.

Отметим, что при n=1 из существования производной следует непрерывность функции.

При даже, если существуют все частные производные f – необязательно является непрерывной.

ПРИМЕР №2.

Решение:

.

Геометрический смысл частных производных

Выясним геометрический смысл частных производных для функции , т.е. .

Геометрическим изображением данной функции является некоторая поверхность S.

Полагая, y=const, :

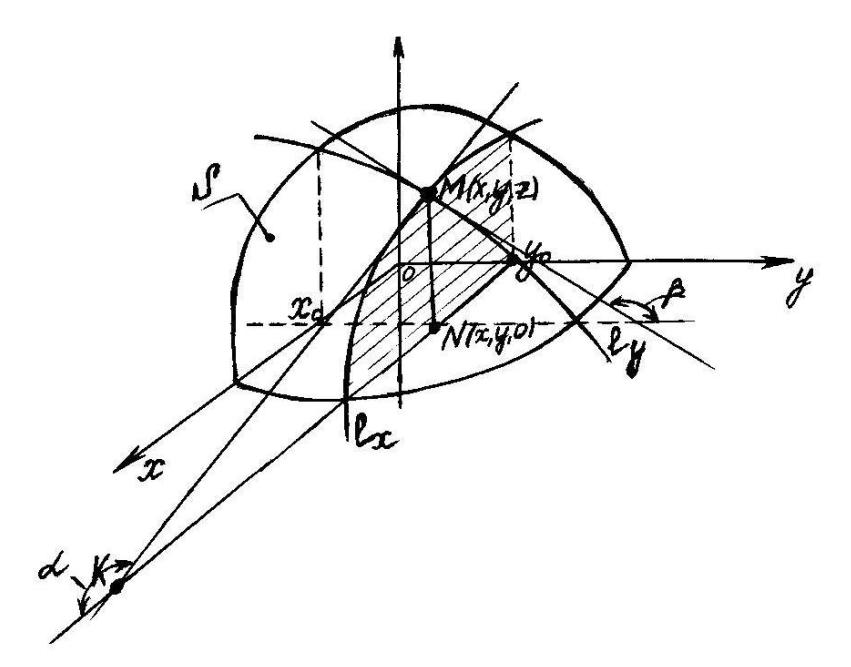
Получим некоторую плоскую кривую , представляющую собой сечение поверхности S соответствующей плоскостью, параллельной координатной плоскости XOZ.

Пусть MK – касательная к кривой в точке M(x,y,z). - угол, образованный этой касательной с положительным направлением оси OX .

Т.к. , то на основании геометрического смысла обычной производной имеем:

Т. о. геометрический смысл частной производной есть тангенс угла наклона, образованного касательной к кривой, лежащей в пересечении поверхности и плоскости в точке и положительным направлением оси OX.

Аналогично, если -есть сечение поверхности S плоскостью и угол -угол, образованный с осью OY касательной ML в точке M(x,y,z) к кривой , то .

Физический смысл частной производной - это скорость изменения функции в точке M в направлении оси .