14. Средние величины: виды и способы вычисления.

Средней величиной называется статистический показатель, который дает обобщенную характеристику варьирующего признака однородных единиц совокупности в конкретных условиях места и времени. Величина средней дает характеристику всей совокупности и характеризует ее в отношении одного, данного признака. Средняя величина отражает то общее, что присуще всем единицам исследуемой совокупности.

Так, например, средняя заработная плата дает обобщающую количественную характеристику состояния оплаты труда рассматриваемой совокупности работников. Кроме того, используя средние величины, имеется возможность сопоставлять различные информационные совокупности. Так, например, можно сравнивать различные организации по уровню производительности труда, а также по уровню фондоотдачи, материалоотдачи и по другим показателям.

Виды средних величин

Средние величины делятся на два больших класса:

• степенные средние

• структурные средние

Степенные средние:

• Арифметическая

• Гармоническая

• Геометрическая

• Квадратическая

Структурные средние:

• Мода

• Медиана

Степенные средние величины

Степенные средние в зависимости от представления исходных данных могут быть простыми и взвешенными. Если вариант встречается один раз, расчеты проводим по средней простой (например зарплата в 3 тыс.руб. встречается только у одного рабочего), а если вариант повторяется неодинаковое число раз, то есть имеет разные частоты (например зарплата в 4 тыс.рублей встречается у пяти работников), то расчет проводим по средней взвешенной.

Самым распространенным видом средней является средняя арифметическая.

Средняя арифметическая простая

Простая среднеарифметическая величина представляет собой среднее слагаемое, при определении которого общий объем данного признака в совокупности данных поровну распределяется между всеми единицами, входящими в данную совокупность. Так, среднегодовая выработка продукции на одного работающего — это такая величина объема продукции, которая приходилась бы на каждого работника, если бы весь объем выпущенной продукции в одинаковой степени распределялся между всеми сотрудниками организации. Среднеарифметическая простая величина исчисляется по формуле:

Простая средняя арифметическая — Равна отношению суммы индивидуальных значений признака к количеству признаков в совокупности

Пример 1. Бригада из 6 рабочих получает в месяц 3 3,2 3,3 3,5 3,8 3,1 тыс.руб.

Найти среднюю заработную плату Решение: (3 + 3,2 + 3,3 +3,5 + 3,8 + 3,1) / 6 = 3,32 тыс. руб.

Средняя арифметическая взвешенная

Если объем совокупности данных большой и представляет собой ряд распределения, то исчисляется взвешенная среднеарифметическая величина. Так определяют средневзвешенную цену за единицу продукции: общую стоимость продукции (сумму произведений ее количества на цену единицы продукции) делят на суммарное количество продукции.

Представим это в виде следующей формулы:

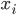• — цена за единицу продукции;

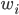• — количество (объем) продукции;

Взвешенная средняя арифметическая — равна отношению (суммы произведений значения признака к частоте повторения данного признака) к (сумме частот всех признаков).Используется, когда варианты исследуемой совокупности встречаются неодинаковое количество раз.

Пример 2. Найти среднюю заработную плату рабочих цеха за месяц

Заработная плата одного рабочего тыс.руб; X	Число рабочих F
3,2	20
3,3	35
3,4	14
4,0	6
Итого:	75

Средняя заработная плата может быть получена путем деления общей суммы заработной платы на общее число рабочих:

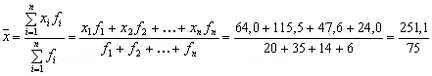
Ответ: 3,35 тыс.руб.

Средняя арифметическая для интервального ряда

При расчете средней арифметической для интервального вариационного ряда сначала определяют среднюю для каждого интервала, как полусумму верхней и нижней границ, а затем — среднюю всего ряда. В случае открытых интервалов значение нижнего или верхнего интервала определяется по величине интервалов, примыкающих к ним.

Средние, вычисляемые из интервальных рядов являются приближенными.

Пример 3. Определить средний возраст студентов вечернего отделения.

Возраст в годах !!х??	Число студентов	Среднее значение интервала	Произведение середины интервала (возраст) на число студентов
до 20	65	(18 + 20) / 2 =19 18 в данном случае граница нижнего интервала. Вычисляется как 20 — (22-20)	1235
20 — 22	125	(20 + 22) / 2 = 21	2625
22 — 26	190	(22 + 26) / 2 = 24	4560
26 — 30	80	(26 + 30) / 2 = 28	2240
30 и более	40	(30 + 34) / 2 = 32	1280
Итого	500		11940

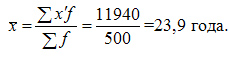
Средняя гармоническая — используется в тех случаях когда известны индивидуальные значения признака и произведение , а частоты неизвестны.

В примере ниже — урожайность известна, — площадь неизвестна (хотя её можно вычислить делением валового сбора зерновых на урожайность), — валовый сбор зерна известен.

Среднегармоническую величину можно определить по следующей формуле:

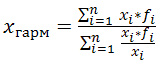
Формула средней гармонической:

Пример. Вычислить среднюю урожайность по трем фермерским хозяйствам

Фермерское хозяйство	Урожайность ц/га (х)	Валовый сбор зерновых Ц (z = x*f)
1	18,2	3640
2	20,4	3060
3	23,5	2350
Итого		9050

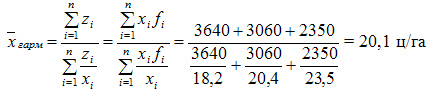
Ответ: 20,1 ц/га

Гармоническая простая

В тех случаях, когда произведение одинаково или равно 1 (z = 1) для расчета применяют среднюю гармоническую простую, вычисляемую по формуле:

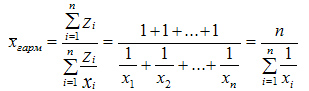
Средняя гармоническая простая — показатель, обратный средней арифметической простой, исчисляемый из обратных значений признака.

Среднегеометрическая величина дает возможность сохранять в неизменном виде не сумму, а произведение индивидуальных значений данной величины. Ее можно определить по следующей формуле:

Среднегеометрические величины наиболее часто используются при анализе темпов роста экономических показателей.

Геометрическая простая

Для расчетов средней геометрической простой используется формула:

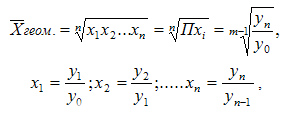
где:

• — цепной коэффициент роста

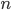• — число этих коэффициентов роста

• П — знак произведения

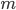• — количество уровней ряда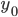

• — значение начального уровня ряда

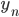• — значение конечного уровня ряда

Геометрическая взвешенная

Для определения средней геометрической взвешенной применяется формула:

Средние диаметры колес, труб, средние стороны квадратов определяются при помощи средней квадратической.

Среднеквадратические величины используются для расчета некоторых показателей, например коэффициент вариации, характеризующего ритмичность выпуска продукции. Здесь определяют среднеквадратическое отклонение от планового выпуска продукции за определенный период по следующей формуле:

Эти величины точно характеризуют изменение экономических показателей по сравнению с их базисной величиной, взятое в его усредненной величине.

Квадратическая простая

Средняя квадратическая простая вычисляется по формуле:

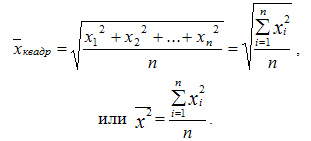
Квадратическая взвешенная

Средняя квадратическая взвешенная равна:

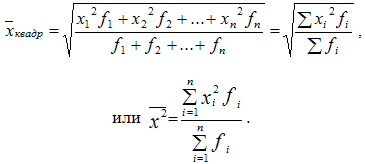
Среднехронологические величины используются для усреднения моментных показателей. Дело в том, что в экономическом анализе и экономической статистике используются как интервальные (за определенный период), так и моментные (на определенную дату) показатели. Чтобы найти средние величины интервальных показателей (выручка от продаж, прибыль и др.) как правило, используют среднеарифметические величины. Для нахождения средних величин моментных показателей (об основных фондах, о численности работников на какую либо-дату, о населении) применяют среднехронологические величины. Их определяют по формуле:

— это ряд моментных показателей

Простая хронологическая средняя

Если интервалы между наблюдениями расположены через равные промежутки времени — то формуле простой хронологической средней:

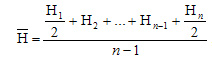
где, , , и — численность населения на каждую дату.

Пример

Численность населения:

• на 1 января 2008 года — 4836 тыс.чел.

• на 1 апреля 2008 года — 4800 тыс.чел.

• на 1 июля 2008 года — 4905 тыс.чел.

• на 1 октября 2008 года — 4890 тыс.чел.

• на 1 января 2009 года — 4805 тыс.чел.

Определить среднюю численность населения за год.

1. Сумму крайних интервалов поделенных на два и внутренних интервалов делим на количество дат отчетности минус один.

СЧН =

Хронологическая взвешенная

В случае если замеры численности населения проводились через неравные промежутки времени то — по формуле хронологической взвешенной:

где:

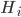• - полусумма двух соседних уровней ряда динамики;

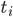• — промежуток между двумя уровнями ряда, выраженный в днях, неделях или месяцах.

Например возьмём промежутки равными месяцам.

СЧН =

Ответ: 4854 чел.