60 Опред-е. Системы векторов

…………………………………

……………………………….

Называются треугольными.

Теорема. Треугольная система векторов ЛНЗ.

Д-во. Рассмотрим

Составляем уравнение линейной зависимости

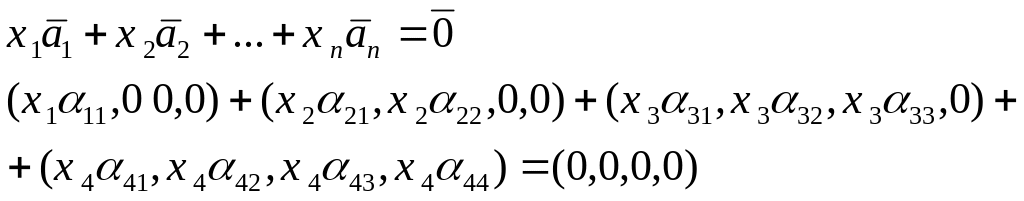
Следовательно, векторы ЛНЗ, т.к. решение только нулевое.

Вопрос № 18.

Теорема о 2-х системах векторов.

Даны 2 системы векторов и , t<k.

Если каждый вектор является ЛК векторов , то система -ЛЗ.

Д-во. Запишем уравнение линейной зависимости

(1) надо показать, что оно имеет ненулевое решение.

Представим в виде ЛК.

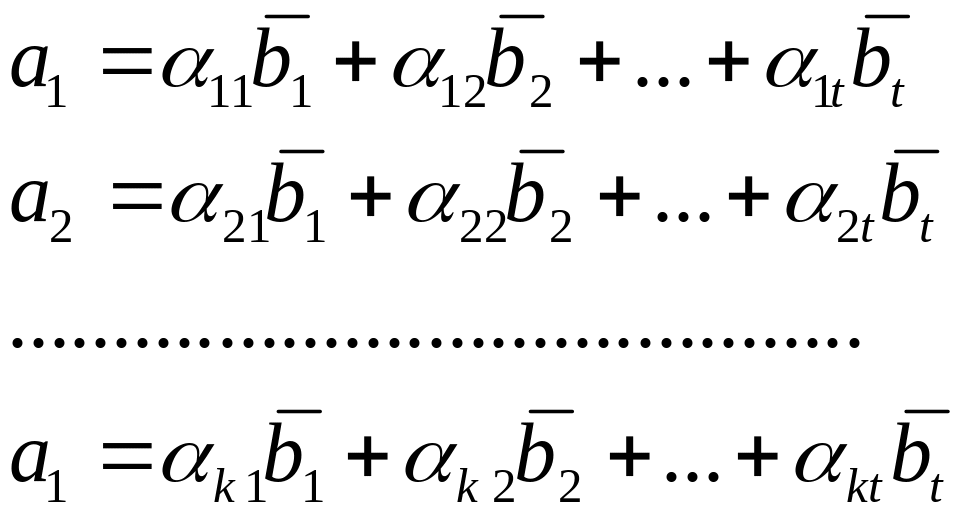(2)

Подставим (2) в (1).

Раскрываем скобки группируем, так чтобы выделить коэффициенты при

Достаточно взять каждый коэф-т при равным нулю.

Получим однородную систему линейных уравнений с k неизвестными (k>t),значит она имеет бесконечно много решений. Значит, есть ненулевое решение. ЧТД.

Вопрос № 21.

Теорема Кронекера - Капелли.

(Критерий совместности системы линейных уравнений)

Система линейных уравнений.

Совместна (т.е. имеет решение)

r(A)=r(A)B).

Доказательство:

Пусть

Столбцы основной матрицы А.

Система может быть переписана в векторном виде.

(1)

Решение (S) является решением (1) и наоборот.

Пусть система (S) совместна.

Тогда - решение (S).

Следовательно - верное векторное равенство. Т. е. вектор - ЛК векторов Т.е.

базис включать не надо, т.к. он выражается через

Следовательно r(А)= r(А(В)

Пусть r(А)= r(А(В))

Тогда

Т.е. вектор в базис не попал, т.е. – ЛК базисных векторов

Значит, существуют числа ,что

Тогда будет верным равенство

Т.е. – решение (1), т.е.это решение (S). Значит, (S) совместна.

Вопрос № 22.

Базис и ранг системы векторов.

Опред 1. Базисом системы векторов называется такая ЛНЗ подсистема, что каждый вектор системы является ЛК вектором подсистемы.

Опр.2. Базисом системы векторов называется максимальная ЛНЗ подсистема, данной системы (т.е. если к максимальной системе ЛНЗ добавить 1 любой вектор, она становится ЛЗ).

Теорема 1.

Опред.1. равносильно опред.2.

Док-во. Пусть дано Опр1, и дана такая ЛНЗ подсистема ,что любой вектор системы её ЛК пусть любой вектор системы. Тогда в-ЛК. Значит, по свойству 1⁰ ЛЗ. Система -ЛЗ. Значит, система была максимальна. Дано опред 2. Пусть - максимальное ЛНЗ подсистема, пусть произведение системы. Тогда система -ЛЗ. Тогда по свойству 5⁰

-ЛК векторов , т.е. мы показали, что любой вектор системы ЛК векторов ЛНЗ подсистемы . Значит, это базис по опр.1. ЧТД.

ОПР. Количество векторов в базисе системы векторов называется рангом системы векторов.

Базис системы векторов определён неоднозначно.

Покажем это на примере.

a₁=(1,1,1) a₁ и а₂-ЛЗ.

а₂=(2,2,2) a₁ и а₃-ЛЗ.

а₃=(1,0,2) a₂ и а₃-ЛЗ.

Значит, - максимальная ЛНЗ подсистема, т.е. базис и - максимальная подсистема, т.е. базис.

Теорема. Ранг системы векторов определен однозначно.

Д-во. Пусть имеется 2 базиса.

и

1) k<t, тогда каждый вектор является ЛК векторов - т.к. Это базис, значит, по теореме о 2-х системах векторов системы ЛЗ, но это базис, значит, они ЛНЗ. Противоречие, т.е. k+t/

2) k>t, тогда каждый вектор является ЛК векторов , т.е. система -ЛЗ по теореме о 2-х системах векторов, но -базис, т.е. ЛНЗ.

Противоречие k>t.

Значит, k=t. ЧТД.

Рассмотрим матрицу

- вектора строки, у каждого n – координат, значит они из . - вектора столбцы, у каждого к координат, т.е. они из

Можно выбрать данные для системы и вычленить ранг. Это будет строчечный ранг матрицы. Можно выбрать базис для системы и вычленить ранг.

Это будет столбцевой ранг матрицы.

ОПР1. Строчечный ранг матрицы – количество ЛНЗ строк.

ОПР.2. Столбцевой ранг – количество ЛНЗ столбцов.

Теорема. Строчечный ранг матрицы равен столбцевому рангу. ( без док-ва)

Элементарные преобразования системы векторов.

1. Поменять 2 вектора в системе номерами (местами)

2. Умножить вектор на любое число ≠0

3. К любому вектору прибавить любой другой вектор, умноженный на любое число.

4. поменять 2 координаты местами

5. Умножить любую координату (одну и ту же у всех векторов) на любое ненулевое число.

6. К любой координате прибавить любую другую координату, умноженную на любое число ( координаты одни и те же у всех векторов)

7. Убрать из системы нулевой вектор.

Теорема. При элементарных преобразованиях ранг системы векторов не меняется. ( без док-ва).

Способ нахождения ранга матрицы.

Применяем к матрице метод Гаусса, используя элементарные преобразования системы векторов, количество оставшихся строк будет рангом матрицы.

Теорема о равенстве нулю определителя.

Теорема. Определитель матрицы А равен 0 , её строки ЛЗ (столбцы ЛЗ).

Доказательство. Пусть А=0, пусть строки ЛНЗ. Тогда ранг равен n. ПО методу Гаусса вычленение ранга матрицы, получим треугольную систему векторов – строк, на диагонали нет нулевых элементов. Определитель при этом не менялся. Он не равен 0, он равен произведению элементов, стоящих на главной диагонали, но он должен быть равен нулю по условию. Противоречие возникло из-за предположения о независимости строк, т.е. строки ЛЗ.

Пусть строки ЛЗ. Тогда одна из строк ЛК остальных. Пусть

Прибавим к 1 –ой строке вторую, умноженную на , получим прибавим к новой 1-ой строке 3-ью, умноженную на и т.д.

В итоге получим определитель с нулевой строкой, он равен нулю, но он не менялся, т.е. он и был равен нулю. ЧТД.

Вопрос № 23.

Понятие векторного пространства.

Базис и размерность векторного пространства.

ОПР. Множество V векторов называется векторным пространством, если V – замкнуто относительно сложения векторов и умножения вектора на число.

Пример 1.

Следовательно, V –векторное пространство.

Пример 2.

Пример 3.

Пример 4. Рассмотрим прямую на плоскости и на ней вектор.

Сумма 2х векторов x опять х и .

Для векторного пространства мы найдём базис – это базис его множества векторов. Ранг векторного пространства называется Размерностью векторного пространства dimV

Т.е. R^{n –} векторное пространство.

Рассмотрим вектора.

Эти векторы ЛНЗ, т.к. они образуют треугольную систему.

Т.е. - базис Rⁿ Значит dim Rⁿ=n.

Линейная оболочка.

ОПР. Линейной оболочкой , натянутой на векторы , называется множество

Теорема.1. Линейная оболочка – векторное пространство.

Д-во.

Теорема 2.

Д-во. Если - ЛНЗ, то они – базис L, т.к. каждый вектор из L их ЛК. Значит, dim L=K.

Если - ЛЗ, то выберем из них максимальную ЛНЗ подсистему, тогда эта подсистема – базис. Тогда dimL<k.

Вопрос № 24.

Однородная система линейных уравнений.

ОПР. Система линейных уравнений называется однородной, если в ней столбец свободных членов нулевой.

Однородная система не может быть несовместной, т.е. она всегда имеет решение.

(0,0,0,..,0) – её решение при любой основной матрице А.

Всегда r(A)=r(A)0), т.е. расширение нулевым столбцом, а нулевой столбец можно убрать из системы как нулевой вектор.

Теорема. Множество решений однородной системы линейных уравнений – векторное пространство. (т.е. сумма решений – решение и произведение решения на число – решение).

Доказательство. Рассмотрим однородную систему:

Пусть

и

и также во 2ом уравнении. Т.е.(с+d)-решение.

Вопрос № 25.

Фундаментальный набор решений однородной системы линейных уравнений (ФНР).

Общее решение.

-общее решение.

ФНР. осб.=0 ост-х нет.

(3,-1,1,-7)

ОПР. ФНР – базис пространства решений однородной системы.

Теорема. Если однородная система линейных уравнений имеет бесконечно много решений, то у неё есть ФНР, который можно построить по следующему правилу.