1. Поменяем местами строки так, что встанет на 1-ое место на 2-ое, на 3-ье,…,

Остальные строки останутся в том же порядке.

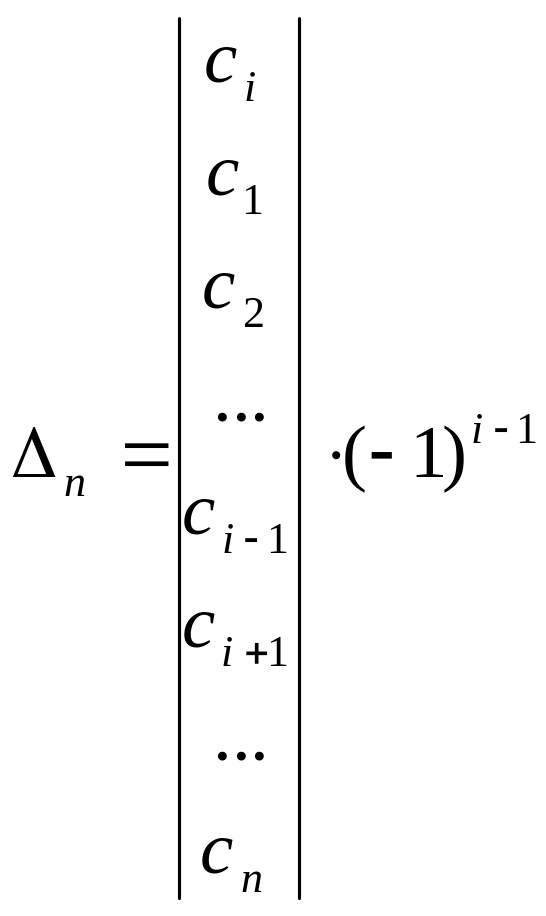
Сколько раз поменялся знак, C_i-2, …, C₁ т.е. всего i-1раз поменяли знак.

вычленяем его разложением по его первой строке.

2.Рассмотрим

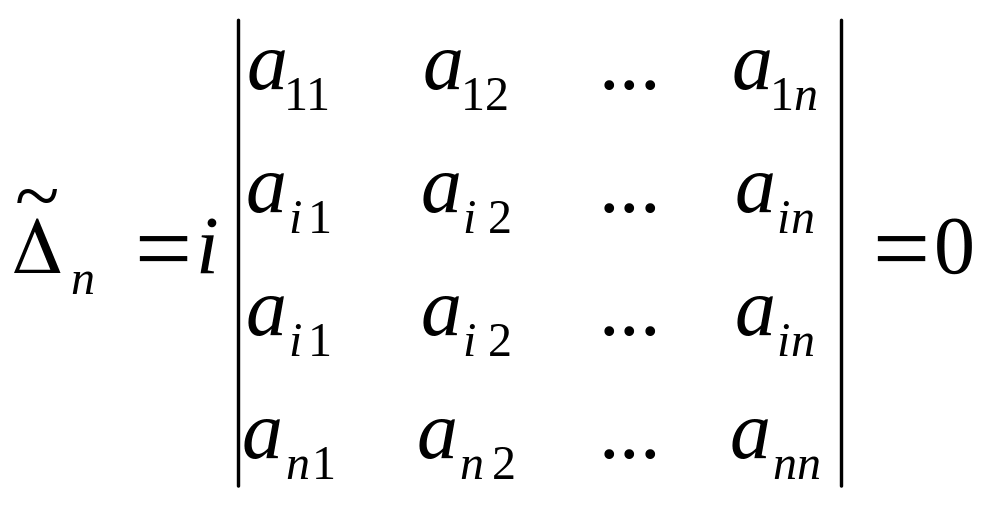
Т.к. у - 2 одинаковые строки, то _n=0. Вычислим его разложением по его к-той строке (получили формулу в 4.1.)

Ч.Т.Д.

Теорема 6’. О разложении по любому столбцу.

1. 2.

Доказательство: Следует из теоремы о транспонировании определителя. Транспонируем определитель ( он при этом не меняется). Столбцы станут строками. Применим теорему о разложении по любой строке. Ч.Т.Д.

(теорема о транспонировании доказана позже)

Вопрос № 10.

Определитель треугольной матрицы.

Определение. Матрица вида

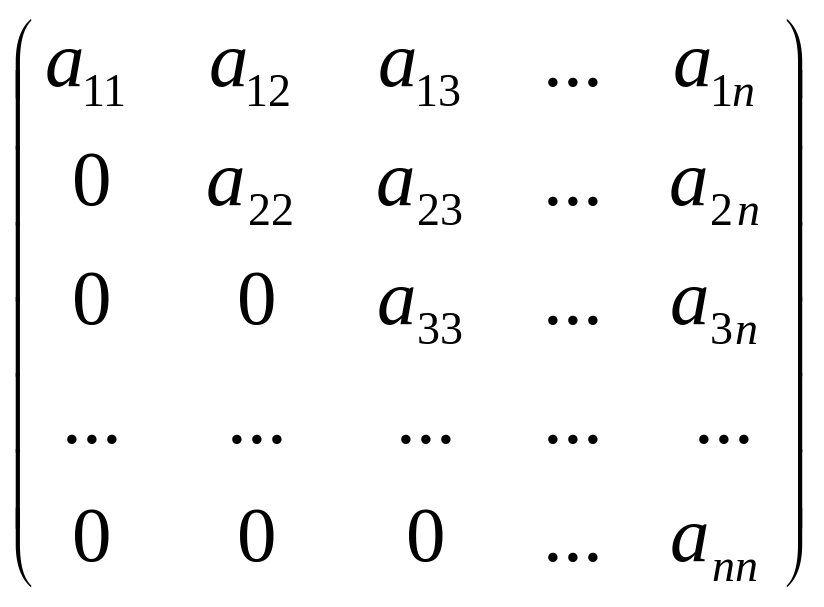называется верхнетреугольной.

Матрица вида

называется нижнетреугольной.

Теорема. Определитель треугольной матрицы равен произведению элементов, стоящих на главной диагонали.

Доказательство: ММИ

2 – пусть теорема верна для определителей порядка n-1.

3. Рассмотрим определитель порядка n.

А) Применим разложение по первой строке.

По индукционному предположению.

ч.т.д.

б) Применим разложение по первой строке.

Порядок n-1, треугольный

для него теорема верна.

В каждом миноре есть нулевой столбец (1-ый). Следовательно они все равны нулю.

Вопрос № 11.

Метод Гаусса.

Будем применять следующие преобразования:

1) поменять две строки (столбца) местами.

2) умножить строку (столбец) на число, не нулевое.

3) к любой строке (столбцу) прибавить любую другую строку (столбец), умноженную на любое число.

Рассмотрим определитель.

Применим к нему метод Гуса.

1 шаг. Смотрим на . Если , то зануляем первый столбец ниже первого места.

Первую строку умножим на и прибавим ко второй,

Первую строку умножим на и прибавим к третей и.т.д. первую строку умножим на и прибавим к n-ой.

Если , то найдем среди элементов первого столбца не нулевой. Поменяем строки местами. Получим и действуем, как описано выше. Если среди элементов первого столбца не нашлось ненулевого, то в определителе есть нулевой столбец. Следовательно, определитель равен 0.

Получим после первого шага.