Вопрос № 1.

Матрицы и действия над ними.

Опр. Матрицей называется прямоугольная таблица.

Размерами k+n.

k- количество строк, n-количество столбцов.

При k=n матрица называется квадратной порядка n.

Элемент стоит в i-той строке и j-том столбце.

Элементы образуют главную диагональ.

Специальные матрицы.

Единичная

квадратная на главной диагонали единицы, а остальные нули.

Нулевая

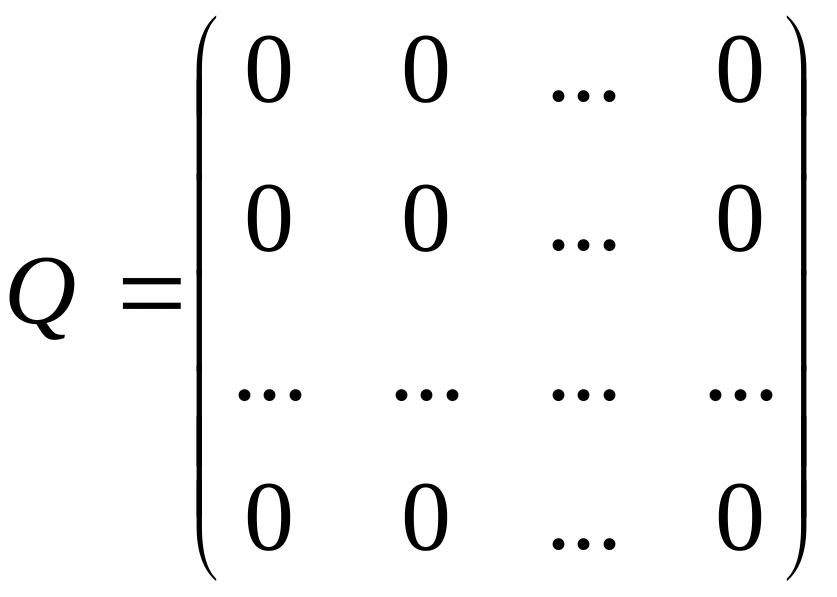
любого размера, все элементы равны 0.

Действия над матрицами.

Две матрицы называются равными, если у них одинаковые размеры и равны элементы стоящие на одинаковых местах.

1) Умножение матрицы на число.

Определение 1. Любую матрицу можно умножить на любое число.

Для этого каждый элемент нужно умножить на это число.

2) Сложение матриц.

Определение 2. Две матрицы одного и того же размера можно сложить.

Для этого нужно сложить элементы, стоящие на одинаковых местах.

Свойства.

1º.

2º.

3º.

4º.

5º.

6º.

Доказательство:

1º.

Обозначим

Надо показать, что

(т.к. это числа)

2º.

Обозначим

(т.к. это число)

3º.

Обозначим

Надо показать, что

(т.к. здесь число)

Вопрос № 2.

2º. Умножение матриц.

Определение 3. Две матрицы A и B можно перемножить, если количество столбцов первой матрицы равно количеству строк второй матрицы.

Свойства.

1º. Умножение матриц не коммутативно, т.е. существуют такие матрицы А и В, что АВ ВА.

Доказательство: Приведём пример.

.

2º. } Дистрибутивность

3º.

4º. Ассоциативность

Доказательство:

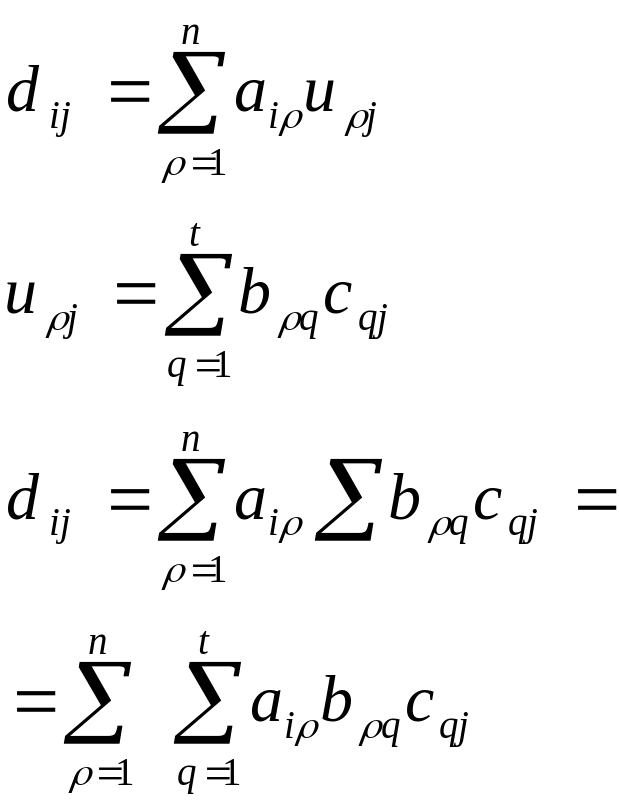
5º. Матрицы называются делителями нуля, если

Во множестве матриц есть делители нуля.

Вопрос № 3.

Определение 1(определители).

Определителем квадратной матрицы называется число, которое получается по следующим правилам.

1. Определитель матрицы порядка 1- это само данное число.

2. Пусть уже определён определитель порядка n-1.

3. Тогда определители порядка n (матрицы порядка n) назовём число

Формула разложения по 1-ой строке.

где определитель порядка n-1 полученный из вычёркиванием первой строки и j- того столбца.

Определители порядка 2.

Определители порядка 3

Определители 2 порядка мы считать уже научились. Значит

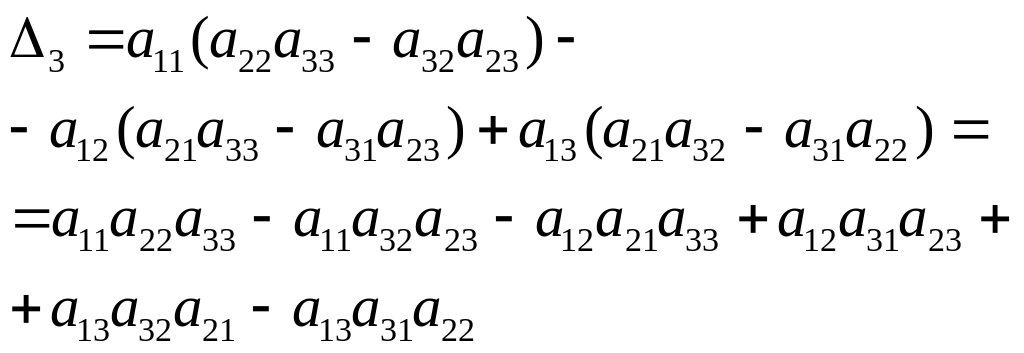
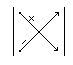
Для вычисления определителей порядка 3 есть “Звездочка”.

-

Докажем это правило.

Сравним со значением , полученным по определению.

Видим, что они равны. Значит, правило “Звездочка” справедливо.

Вопрос № 4.

Определитель с нулевой строкой (столбцом).

Теорема 1. Если в определителе есть нулевая строка, то этот определитель равен нулю.

Доказательство: ММИ.

1 шаг.

2 шаг. Пусть теорема доказана для определителей порядка n-1 , т.е. если в определителе порядка n-1 есть нулевая строка, то этот определитель равен нулю.

3 шаг. Рассмотрим определитель порядка n.

1 случай. Нулевая строка первая.

2 случай. Нулевая строка не первая.

В каждом миноре есть нулевая строка, - определитель порядка n-1 для него теорема верна

Теорема 1’. Если в определителе есть нулевой столбец, то определитель равен нулю. Доказательство: ММИ.

1 шаг.

2 шаг. Пусть для определителей порядка n-1 теорема доказана.

3 шаг. Рассмотрим определитель порядка n. (Пусть нулевой столбец второй).

В каждом миноре есть нулевой столбец. Значит =0 по индукционному предположению, т.к. - определитель порядка n-1. Отсюда .

Вопрос № 5.

Умножение строки (столбца) определителя на число.

Теорема 2.

Если строку определителя умножить на число, то весь определитель умножится на это число. (Из строки определителя можно вынести общий множитель за знак определителя).

Доказательство: ММИ.

1 шаг. Ч.Т.Д.

2 шаг. Пусть теорема доказана для определителей порядка n-1.

3 шаг. Рассмотрим определитель порядка n.

1 случай. На умножили первую строку.

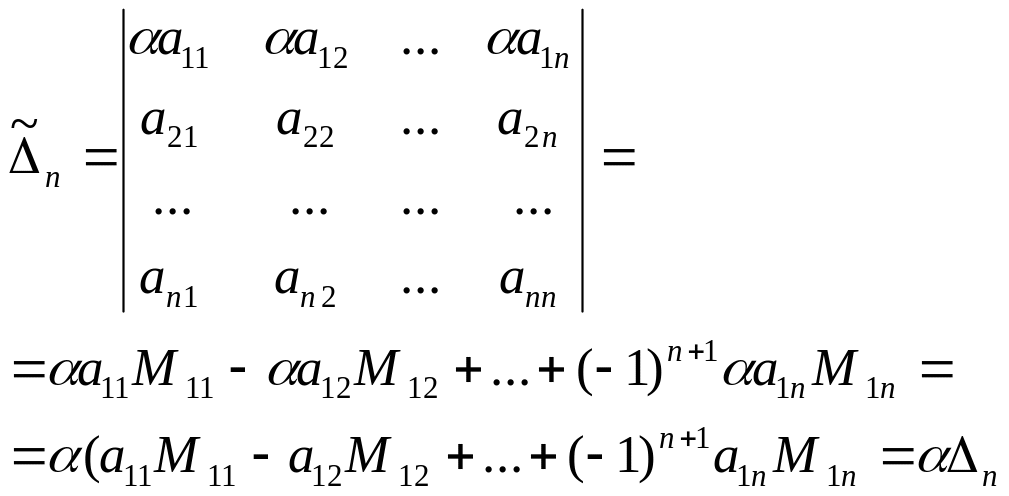
2 случай. На умножена не первая строка.

Каждый минор содержит строку, умноженную на число ,

- определитель порядка n-1.

Для определителя порядка n-1 теорема справедлива, отсюда = .

Тогда

Теорема 2’.

Если столбец определителя умножить на число , то весь определитель умножится на . (Из столбца можно вынести общий множитель за знак определителя).

Доказательство:

1 шаг. n=1 Самостоятельно.

2 шаг. Пусть для определителей порядка n-1 теорема доказана.

3 шаг. Рассмотрим определитель порядка n. (Пусть на умножен третий столбец).

Каждый минор содержит столбец умноженный на .

Следовательно, по индукционному предположению = .

Отсюда

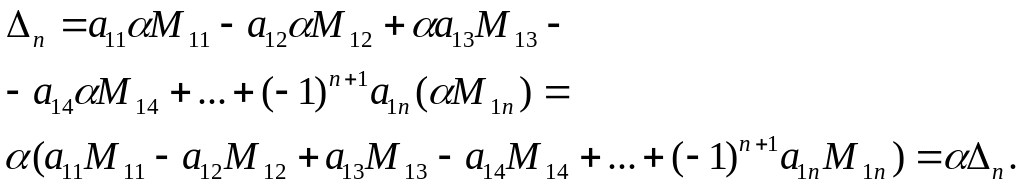
Вопрос № 6.

Теорема 3. Сложения определителей (для строк).

Если в определителе одна из строк представлена в виде суммы 2-х слагаемых, то определитель равен сумме 2-х определителей, в первом из в данной строке стоит 1-ое слагаемое, а во 2-ом в данной строке стоит другое слагаемое. Все остальные строки у этих определителей такие же, как в исходном определителе.

Пусть 1-ая строка в виде суммы.

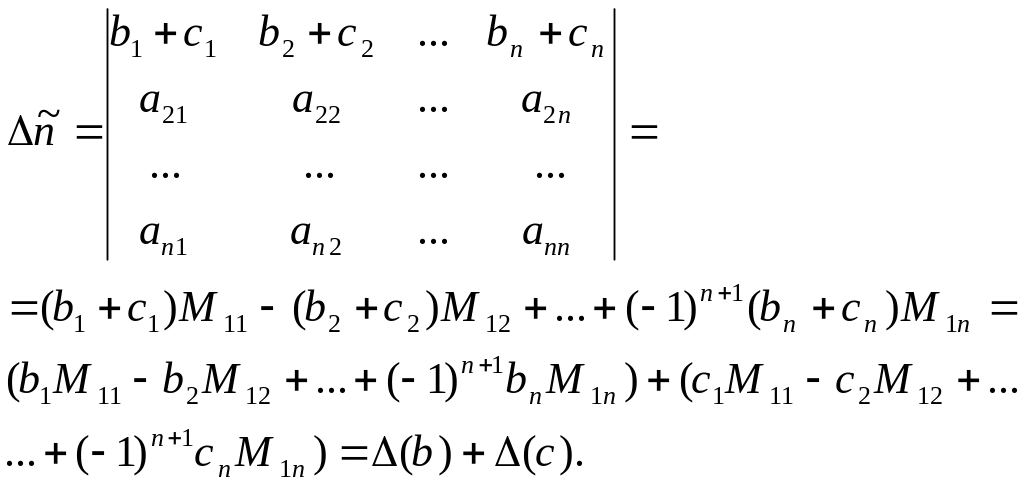
Пусть строка не 1-ая.

т.к. миноры ( ) - это определители порядка n-1 , то для них теорема доказана.

Теорема 3’.

Теорема сложения определителей (для столбцов).

Если в определителе 1 из столбцов представлен в виде суммы 2-хслогаемых, то определитель равен сумме 2-х определителей, в первом из в данном столбце стоит 1-ое слагаемое, а во 2-ом в данном столбце стоит другое слагаемое. Все остальные столбцы у этих определителей такие же как в исходном определителе.

Доказать: ММИ.

1.