26. Гипотезы согласия и критерии согласия. Критерий Хи-квадрат Пирсона как критерий согласия. Критерий согласия ω2. Критерий согласия Колмогорова.

Это частный случай гипотез и критериев значимости.

Гипотеза согласия – гипотеза, предполагающая, что теоретическая функция распределения имеет конкретный вид , т.е. (проверка на принадлежность к какому-либо классу). Критерии для таких гипотез называются критериями согласия.

Предположим, что имеется выборка x₁,…,x_n объема n из генеральной совокупности с неизвестной функцией распределения F(x). H₀ : F(x)=F⁰(x), где F⁰(x) – заданный закон распределения (функция распределения).

Гипотеза такого вида называется гипотезой согласия, а критерий для проверки гипотезы согласия называется критерием согласия.

Критерий согласия X²-Пирсона.

В критерии X²- Пирсона в качестве меры отклонения теоретической функции распределения F(x) от эмпирической функции распределения F_n(x) выбирается величина

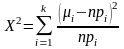
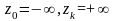
Обозначим через , - число выборочных значений, попавших в интервал ,

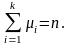
Теорема (Пирсона).

Пусть , тогда , где случайная величина 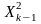имеет распределение X² с (k-1) степенью свободы. , тогда 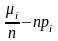- мало X² – небольшое число. Если предположим, что H₀ – верна, то . Задаем уровень значимости . , (% точка распределения X²).

Если 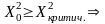гипотеза H₀ отвергается. Если H₀ согласуется с экспериментальными данными.

Алгоритм следующий:

1. Разбиваем всю числовую ось на k интервалов (отрезков).

2. Находим

3. Производим расчет вероятностей

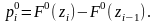
4. Рассчитываем

5. По таблице процентных точек распределения X² находим X²_{критическое}:

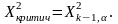
6. Проверяем: - H₀ – отвергается; - H₀ – согласуется с экспериментальными данными.

Замечание: Пусть закон распределения зависит от m неизвестных параметров. Тогда эти параметры заменить их оценками и проверить нулевою гипотезу в виде: . Тогда оказывается, что теорема Пирсона будет верна с некоторыми поправками и примет вид: 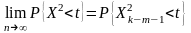. Поэтому предварительно находятся оценки параметров и .

Критерии ω².

Пусть x₁,…,x_n – выборка из генеральной совокупности с неизвестной функцией распределения F(x). Проверить .

В качестве меры отклонения теоретической функции от эмпирической , где – k-ый член вариационного ряда 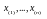, т.е. . Обозначим через .

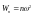Теорема (Смирнова). Если функция распределения F(x) непрерывна, то , который не зависит от вида функции распределения F(x).

Имеются таблицы процентных точек, позволяющее находить -% точка).

1. Находим

2. Находим по таблице.

3. Если , то H₀ отвергается.

Если , то H₀ согласуется с экспериментальными данными.

Критерий Колмогорова.

Имеется выборка x₁,…,x_n и H₀: F(x)=F⁰(x). В качестве меры отклонения теоретической функции распределения F(x) берется .

Теорема (Колмогорова).

Если F(x) непрерывна, то . Имеются таблицы процентных точек распределения Колмогорова.

- процентная точка распределения Колмогорова, соответствующая уровню значимост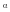и или .

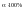Алгоритм:

1. Считаем .

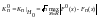2. Если 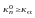, то H₀ отвергается.

Есл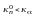и , то H₀ согласуется с экспериментальными данными.