
- •Свойства функции распределения.
- •Свойства плотности распределения.
- •Функция распределения случайного вектора неубывающая по каждому аргументу.
- •Свойства математического ожидания:
- •Математическое ожидание постоянной величины равно самой постоянной:
- •Постоянный множитель можно выносить за знак математического ожидания:
- •Свойства дисперсии.
- •Свойства корреляции.
- •Свойства производящих функций.
- •Свойства характеристических функций.
- •17.Законы больших чисел в форме Чебышева и Бернулли. Неравенство Чебышева.
- •21 Методы получения точечных точечных оценок неизвестных параметров. Метод моментов. Метод максимального правдоподобия
- •22.Информация о выборке по Фишеру в выборке и в наблюдении. Неравенство Рао-Крамера. Доказательство эффективности оценок при помощи неравенства Рао-Крамера.
- •23.Распределение c2, Стьюдента, Фишера. Критические (процентные) точки. Леммы о нормальном распределении и Фишера.
- •24.Понятие многомерного нормального распределения. Лемма Фишера. Следствие из Леммы Фишера.
- •25. Определение одностороннего и двустороннего доверительных интервалов. Точность интервальной оценки. Надежность. Лемма о равномерном распределении. Основная теорема интервального оценивания.
- •Гипотезы согласия и критерии согласия. Критерий Хи-квадрат Пирсона как критерий согласия. Критерий согласия ω2. Критерий согласия Колмогорова.
- •Теорема (Пирсона).
- •Понятие, сущность и задачи дисперсионного анализа. Однофакторный дисперсионный анализ. Групповые средние. Проверка гипотезы о равенстве групповых средних.
- •Корреляционный анализ.
- •Регрессия. Основная теорема регрессионного анализа. Метод наименьших квадратов. Выборочные уравнения линейной регрессии.
17.Законы больших чисел в форме Чебышева и Бернулли. Неравенство Чебышева.
Последовательность случайных величин Х1, Х2,… называется сходящейся по вероятности к случайной величине Х, если для любого положительного числа , т.е.
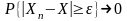 при
.
Обозначается
при
.
Обозначается
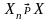 .
.
Говорят, что последовательность случайных величин Х1, Х2,… удовлетворяют закону больших чисел, если
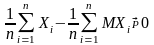 .
.
Теорема
1. Для любой
случайной величины Х, имеющей конечную
дисперсию DX,
справедливо неравенство Чебышёва:Для
.
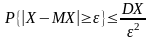 .
.
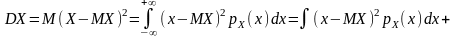
{x││x-MX│≥ε}
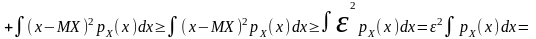
{x││x-MX│≥ε} {x││x-MX│≥ε} {x││x-MX│≥ε} {x││x-MX│≥ε}
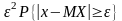 .
.
Таким
образом,
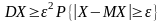
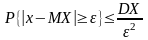 .
.
Теорема 2. (закон больших чисел в форме Чебышёва).
Пусть
Х1,Х2,…—последовательность
попарно независимых случайных величин,
имеющих конечные дисперсии, ограниченные
одной и той же постоянной, т.е.
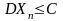 .
Тогда эта последовательность удовлетворяет
закону больших чисел.
.
Тогда эта последовательность удовлетворяет
закону больших чисел.
Обозначим через
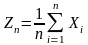 .
Нужно доказать, что
.
Нужно доказать, что
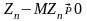 .
.
 .
.
Отсюда
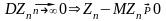 (т.к.
(т.к.
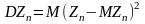 ).
).
Теорема 3. (Закон больших чисел в форме Бернулли).
Пусть μ—число
успехов в n
независимых испытаниях Бернулли с
вероятностью успеха р в одном испытании,
тогда
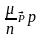 .Таким
образом, закон больших чисел в форме
Бернулли теоретически подтверждает
устойчивость относительных частот,
т.е. стабилизацию при большом числе
испытаний относительной частоты вокруг
вероятности (относительная частота
≈Р(А)).
.Таким
образом, закон больших чисел в форме
Бернулли теоретически подтверждает
устойчивость относительных частот,
т.е. стабилизацию при большом числе
испытаний относительной частоты вокруг
вероятности (относительная частота
≈Р(А)).
18.Условия сходимости функции распределения одинаково распределенных слагаемых к функции стандартного нормального распределения. Сходимость функций распределения разнораспределенных слагаемых к нормальному закону.
Центральная предельная теорема.
Теорема. (Ц.П.Т.).
Пусть
Х1,Х2,…—последовательность
независимых случайных величин, имеющих
один и тот же закон распределения и
конечное математическое ожидание а
и дисперсию G2.
Тогда при
вероятность того, что
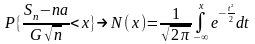 ,
где
,
где
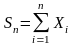 .
.
N(x)—функция стандартного нормального распределения.
Замечание 1. Центральная предельная теорема обосновывает тот факт, что нормальное распределение встречается в природе чаще других.
Замечание
2. При больших
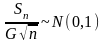 ,
поэтому
,
поэтому
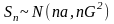 .
ЦПТ можно записать в другой форме:
.
ЦПТ можно записать в другой форме:
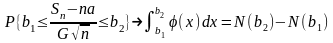 .
.
19.Предмет и задачи математической статистики. Выборка, генеральная совокупность, объем совокупности. Конкретная и абстрактная выборки. Эмпирическая случайная величина. Эмпирическая функция распределения. Повторная и бесповторная выборка. Вариационный ряд выборки. Выборочные моменты. Полигон и гистограмма частот и относительных частот.
О. МС – наука о способах получения, сокращения, хранения и обработки информации.Установление закономерностей, которым подчинены массовые случайные явления, основано на изучении методами теории вероятностей статистических данных – результатов наблюдений.Первая задача математической статистики - указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или в результате специально поставленных экспериментов.Вторая задача МС - разработать методы анализа статистических данных в зависимости от целей исследования. Сюда относятся: а) оценка неизвестных параметров;б) проверка статистических гипотез ;в) установление статистических зависимостей между случайными событиями, случайными величинами или случайными процессами (регрессионный, корреляционный, дисперсионный, дискриминантный анализ);г) управление случайными процессами;д) планирование эксперимента;
Генеральная совокупность. Выборка.
О. Выборочной совокупностью или просто выборкой называют совокупность случайно отобранных объектов.
О. Генеральной совокупностью называется совокупность объектов, из которых производится выборка.
О. Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности.
Предположим, что
можем производить измерения случайной
величины Х. Допустим, что в n
экспериментах результаты измерений
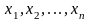 - некоторые числа.
- некоторые числа.
Предполагаем, что выполняются следующие две предпосылки:
Эксперименты проводятся в одинаковых условиях;
Эксперимента проводятся независимо друг от друга.
О. Говорят, что результаты n экспериментов образуют конкретную выборку объема n из генеральной совокупности случайной величины Х, если выполняются предпосылки 1 и 2. Величину Х называют теоретической случайной величиной.
О. Говорят,
что случайные величины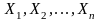 образуют абстрактную
выборку объема n,
если они независимы и одинаково
распределены.
образуют абстрактную
выборку объема n,
если они независимы и одинаково
распределены.
О. Функция распределения F(x) случайной величины Х называется теоретической функцией распределения или функцией распределения генеральной совокупности.
Как абстрактную, так и конкретную выборку будем обозначать одними и теми же буквами и называть выборкой.
О. Повторной называют выборку, при которой отобранный объект (перед отбором следующего ) возвращается в генеральную совокупность.
О. Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается.
Эмпирические функции распределения. Полигон и гистограмма.
Предположим, что имеется выборка из генеральной совокупности с функцией распределения F(x).
Через Y обозначим случайную величину с рядом распределения (законом распределения)
Y |
x1 |
x2 |
... |
xn |
P |
1/n |
1/n |
... |
1/n |
О. Случайная величина Y называется выборочной или эмпирической. Ряд распределения случайной величины Y называется выборочным или эмпирическим.
О. Числовые характеристики теоретической СВ Х называются генеральными характеристиками.
О. Числовые характеристики эмпирической случайной величины Y называются выборочными.
О. Генеральным начальным элементом к-го порядка называется число bk=MXk.
О.
Выборочным
начальным моментом к-го порядка
называется число
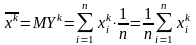 .
.
О.
Выборочной
средней
называется среднее арифметическое
выборочного ряда распределения, т.е.
 .
.
О. Генеральным центральным моментом к-го порядка называется число
mk=M(X-MX)k
О. Выборочным центральным моментом к-го порядка называется число
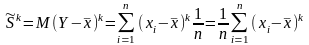 .
.
В частности,
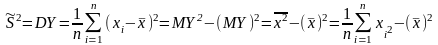 -
выборочная
дисперсия
-
выборочная
дисперсия
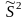 - оценка генеральной
дисперсии
- оценка генеральной
дисперсии
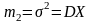
О. Эмпирической функцией распределения называется функция распределения выборочной (эмпирической) случайной величины Y. Обозначается эта функция:
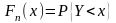 .
.
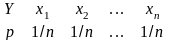
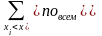 , где
, где
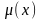 - число выборочных значений
- число выборочных значений
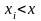
О.
Последовательность значений
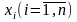 ,
записанных в возрастающем порядке
,
записанных в возрастающем порядке
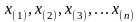 где
где
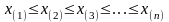 называется вариационным
рядом выборки.
называется вариационным
рядом выборки.
О.
Наблюдаемые значения
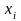 называют вариантами.Числа
наблюдений
называют вариантами.Числа
наблюдений
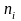 называют частотами,
а их отношения к объему выборки
называют частотами,
а их отношения к объему выборки
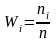 - относительными
частотами.
- относительными
частотами.
О.Полигоном
частот
называют ломаную, отрезки которой
соединяют точки
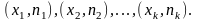 Для
построения полигона частот на оси
абсцисс откладывают варианты
,
а на оси ординат – соответствующие им
частоты
.
Точки
Для
построения полигона частот на оси
абсцисс откладывают варианты
,
а на оси ординат – соответствующие им
частоты
.
Точки
 соединяют отрезками и получают полигон
частот.
соединяют отрезками и получают полигон
частот.
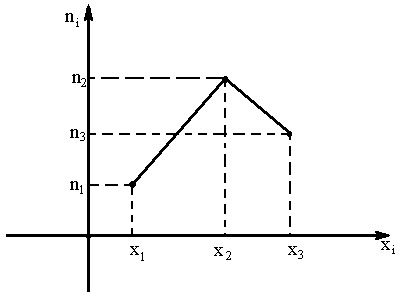
О.
Полигоном
относительных частот
называют ломаную, отрезки которой
соединяют точки
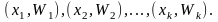
Предположим,
что
- выборка из непрерывной генеральной
совокупности с плотностью вероятности
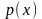 .
Необходимо построить оценку плотности
.
.
Необходимо построить оценку плотности
.
Интервал, в котором заключены все наблюдаемые значения, разбиваем на k частичных интервалов длины
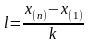 ,
где
,
где
 - наибольшая, а
- наибольшая, а
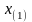 - наименьшая из вариант,
- наименьшая из вариант,
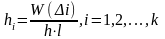 ,
где
,
где
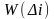 - число выборочных значений, попадающих
в i
– й интервал
- число выборочных значений, попадающих
в i
– й интервал
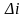 ,
n
– объем выборки.
,
n
– объем выборки.
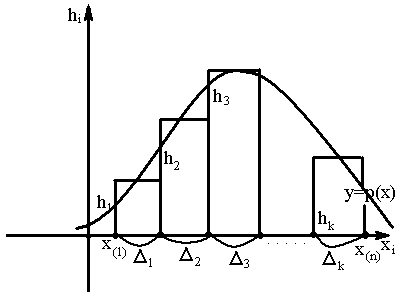
Полученная ступенчатая фигура называется гистограммой относительных частот.
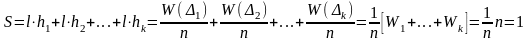
О.Гистограммой
частот
называют ступенчатую фигуру, состоящую
из прямоугольников, основаниями которых
служат частичные интервалы длиной
,
а высоты равны отношению
 (вместо
(вместо
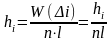 )
)
Площадь
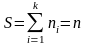 ,
т.е. равна сумме всех частот, т.е. объему
выборки.
,
т.е. равна сумме всех частот, т.е. объему
выборки.
20 Точечная оценка неизвестного параметра. Определение несмещенности, состоятельности и эффективности оценки. Несмещенность выборочной средней и исправленной выборочной дисперсии. Несмещенность, состоятельность, эффективность эмпирической функции распределения
Точечные оценки неизвестных параметров. Несмещенные, состоятельные и эффективные оценки.
Предположим, что
имеется выборка
из генеральной совокупности, закон
распределения которой зависит от
неизвестного параметра
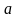 (например,
функция распределения
(например,
функция распределения
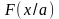 ).
).
О1.
Оценкой или
статистикой
параметра
называется любая функция
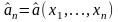 от выборочных значений
.
от выборочных значений
.
О2.
Оценка
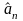 неизвестного
параметра
называется несмещенной,
если математическое ожидание
неизвестного
параметра
называется несмещенной,
если математическое ожидание
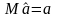 .
.
О3.
Оценка
неизвестного параметра
называется состоятельной,
если
сходится по вероятности k
a
( т.е. для
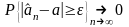 )
)
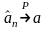 .
.
О4. Несмещенная оценка неизвестного параметра называется эффективной, если она имеет наименьшую дисперсию среди всех несмещенных оценок параметра .
┐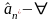
 несмещенная оценка
параметра
,
тогда
эффективна, если
несмещенная оценка
параметра
,
тогда
эффективна, если
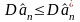
Пример:
Предположим, что имеется выборка
из генеральной совокупности с
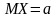 ,
,
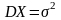 .
Здесь
-
генеральная средняя,
.
Здесь
-
генеральная средняя,
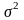 - генеральная дисперсия.
- генеральная дисперсия.
В
качестве оценки
возьмем
выборочную среднюю
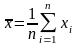 .
В качестве оценки
возьмем
выборочную дисперсию
.
В качестве оценки
возьмем
выборочную дисперсию
 .
Проверим, насколько хороша оценка
.
Проверим, насколько хороша оценка
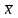 :
:
1.
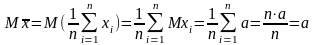
Вывод: - несмещенная оценка параметра .
2.
Поскольку
- независимы,
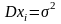 .
По закону больших чисел в форме Чебышева
.
По закону больших чисел в форме Чебышева
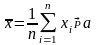
По определению 3 - состоятельная оценка параметра .
3. Эффективность оценки зависит от закона распределения генеральной совокупности.
Оценка .
1.
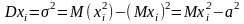 .
.
Следовательно,
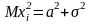 (1)
(1)
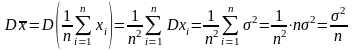 .
.
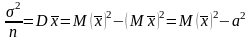
Следовательно,
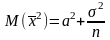 (2)
(2)
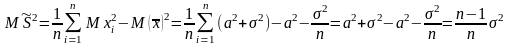
Следовательно, не является несмещенной оценкой. При оценка будет почти несмещенной.
2.
Можно проверить, что
- состоятельная. Введем
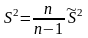 ,
тогда
,
тогда
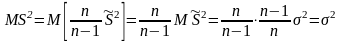
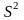 - несмещенная
оценка и называется исправленной
выборочной дисперсией.
- несмещенная
оценка и называется исправленной
выборочной дисперсией.
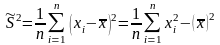 - неисправленная
выборочная дисперсия.
- неисправленная
выборочная дисперсия.
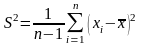 - исправленная
выборочная дисперсия.
- исправленная
выборочная дисперсия.
Пусть
- выборка из генеральной совокупности
с функцией распределения
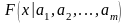 ,
зависящей от
,
зависящей от
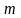 неизвестных
параметров. Необходимо найти оценки
неизвестных
параметров. Необходимо найти оценки
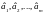 параметров
параметров
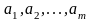 .
.
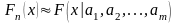 при больших
при больших
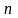 .
.
Более
того, можно рассматривать
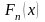 как оценку
или
как оценку
или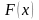 при каждом фиксированном значении
при каждом фиксированном значении
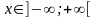 .
.
Поскольку
- результаты n
испытаний для случайной величины
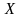 ,
то в качестве успеха в случайном испытании
примем:
,
то в качестве успеха в случайном испытании
примем:
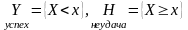 .
.
Тогда
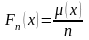 ,
где
,
где
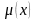 - число выборочных значений, меньших
- число выборочных значений, меньших
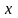 ,
т.е. число успехов.
,
т.е. число успехов.
 , где
, где
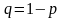 ,
,
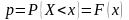 .
.
Таким образом,
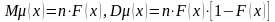 .
.
Следовательно,
1.
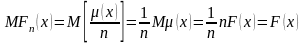
При любом фиксированном является несмещенной оценкой .
2.
Проверим состоятельность оценки

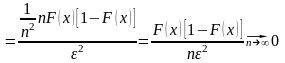 т.к.
т.к.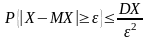 ,
,
если
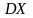 -
конечно.
-
конечно.
По
теореме о двух милиционерах
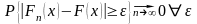 .
.
Т.о.
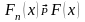 ,
т.е.
- состоятельная оценка
.
,
т.е.
- состоятельная оценка
.
3. Оказывается, что эта оценка является также и эффективной.
