
- •Свойства функции распределения.
- •Свойства плотности распределения.
- •Функция распределения случайного вектора неубывающая по каждому аргументу.
- •Свойства математического ожидания:
- •Математическое ожидание постоянной величины равно самой постоянной:
- •Постоянный множитель можно выносить за знак математического ожидания:
- •Свойства дисперсии.
- •Свойства корреляции.
- •Свойства производящих функций.
- •Свойства характеристических функций.
- •17.Законы больших чисел в форме Чебышева и Бернулли. Неравенство Чебышева.
- •21 Методы получения точечных точечных оценок неизвестных параметров. Метод моментов. Метод максимального правдоподобия
- •22.Информация о выборке по Фишеру в выборке и в наблюдении. Неравенство Рао-Крамера. Доказательство эффективности оценок при помощи неравенства Рао-Крамера.
- •23.Распределение c2, Стьюдента, Фишера. Критические (процентные) точки. Леммы о нормальном распределении и Фишера.
- •24.Понятие многомерного нормального распределения. Лемма Фишера. Следствие из Леммы Фишера.
- •25. Определение одностороннего и двустороннего доверительных интервалов. Точность интервальной оценки. Надежность. Лемма о равномерном распределении. Основная теорема интервального оценивания.
- •Гипотезы согласия и критерии согласия. Критерий Хи-квадрат Пирсона как критерий согласия. Критерий согласия ω2. Критерий согласия Колмогорова.
- •Теорема (Пирсона).
- •Понятие, сущность и задачи дисперсионного анализа. Однофакторный дисперсионный анализ. Групповые средние. Проверка гипотезы о равенстве групповых средних.
- •Корреляционный анализ.
- •Регрессия. Основная теорема регрессионного анализа. Метод наименьших квадратов. Выборочные уравнения линейной регрессии.
Свойства дисперсии.
Дисперсия постоянной величины С равна 0. DC=0.
Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
 .
.
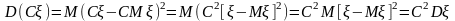 .
.
Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:
 .
.

Следствие. Дисперсия суммы нескольких независимых случайных величин равна сумме дисперсий этих величин.
Коэффициентом корреляции между случайными величинами и называется число
 .
.Ковариацией между случайными величинами и наз-ся такое число

Свойства корреляции.
Абсолютная величина коэффициента корреляции не превосходит единицы, т.е.
 .
.Для того чтобы
 необходимо и достаточно, чтобы случайные
величины
и
были связанны линейной зависимостью.
Т.е.
необходимо и достаточно, чтобы случайные
величины
и
были связанны линейной зависимостью.
Т.е. с вероятностью 1.
с вероятностью 1.Если случайные величины независимы, то они некоррелированы, т.е. r=0.
Пусть
и
—независимы, тогда по свойству
математического ожидания

№15.
Под целочисленной случайной величиной будем понимать дискретную случайную величину, которая может принимать значения 0,1,2,…
Таким образом, если случайная величина —целочисленная, то она имеет ряд распределения
|
0 |
1 |
2 |
… |
Р |
р0 |
р1 |
р2 |
… |
Пусть —целочисленная величина с законом распределения
|
0 |
1 |
2 |
… |
Р |
р0 |
р1 |
р2 |
… |
Ее
производящей функцией называется
функция

Свойства производящих функций.
Производящая функция
 определена в области
определена в области
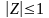 .
.Производящая функция

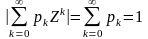
Значение производящей функции в точке Z=1, P(1)=1.
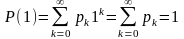 .
.Если Z=1, то M =P’(1)
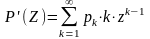 .
.
 .
.
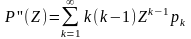 .
Если Z=1
.
Если Z=1
 .
.
 .
.
Следовательно,
 .
.
Если Х1,Х2,…,Хn—независимые целочисленные случайные величины, то производящая функция
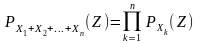 .
.

 .
.
Характеристической функцией случайной величины называется функция
 ,
где
,
где
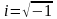 .
.
Формулы для вычисления характеристической функции.
Случай 1. Пусть —дискретная случайная величина с рядом распределения
|
x1 |
x2 |
… |
Р |
p1 |
p2 |
… |
 .
.
Случай
2. Пусть
—целочисленная
случайная величина с плотностью
 .
Тогда характеристическая функция
.
Тогда характеристическая функция
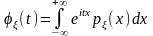 .
.
Свойства характеристических функций.
Характеристическая функция определена для любой случайной величины. При этом
 ,
,
 .
.
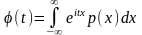 .
.
 .
.
Поскольку
 ,
то
,
то

Характеристическая функция случайной величины
 ,
где a,
b—некоторые
числа.
,
где a,
b—некоторые
числа.
 .
.
 .
.
Если случайные величины —независимы, то характеристическая функция суммы данных случайных величин равна произведению характеристических функций этих случайных величин, т.е.

 .
.
Если М
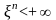 ,
характеристическая функция случайной
величины
n
раз дифференцируема, причем
,
характеристическая функция случайной
величины
n
раз дифференцируема, причем
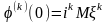 ,
где
,
где
 .
.
Замечание. Необходимо отметить, что функция распределения величины однозначно определяется характеристической функцией. Таким образом, характеристическая функция является законом распределения случайной величины.
Свойство
5.

Свойство
6. Если
случайные величины
и
независимы, то производящая ф-я
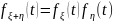
№16.
Пусть
,
где
 -случайная
величина наз-ся случайной
последовательностью.
-случайная
величина наз-ся случайной
последовательностью.
Последовательность
случайных величин
называется
сходящейся
по вероятности
к случайной величине
если для любого положительного числа
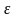 ,
т.е.
,
т.е.

 при
при
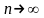 .
Обозначается
.
Обозначается
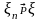 .
.
Опр.Говорят,
что последовательность
 сход-ся к случайной величине
слабо, если последовательность фун-и
распределения
сход-ся к случайной величине
слабо, если последовательность фун-и
распределения
 cлабо
сход-ся к
cлабо
сход-ся к
 .
.
Говорят,
что последовательность
случайных
величин удовлетворяют
закону больших чисел,
если
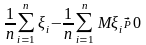 .
.
Т-а. Пусть { }- последовательность независимых случ-х величин, имеющих конечные дисперсии, ограниченные одной и той же константой, тогда эта последовательность удовлетворяет закону больших чисел.

