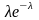№1. Терминология теории вероятностей. Предмет и задачи теории вероятностей. События, операции над событиями. Невозможное и достоверное события. Гипотезы. Определение вероятности события.
Теория вероятностей- математич. Наука, изучающая закономерности случайных явлений, в кот. проявляется статистическая регулярность.
Одна из основных задач теории вероятностей состоит в выяснении закономерностей, возникающих при взаимодействии большого числа случайных факторов. Методы теории вероятностей играют важную роль при обработке статистических данных.
Опр
Первичным
понятием неопределемым через другие
явл. понятие пр-ва
элем-ых исх-ов.
Это некот. мн-во состоящее из эл-ов
,
кот-ые наз-ются элем-ми
исходами. Элем-ые
исходы соотв-ют единственно-возможным
результ. эксперимента.
Опр Событием наз-ся произвольное подмн-во А пр-ва элем-ных исходов Ω.
Элем-ные исходы, из кот-ых состоит соб. А, наз-ются благоприятствующими соб-ию А.
Если -конечно, пересчётно, то его наз-ют дискретным.
Опр Говорят, что соб. А происх., если в результ. Эксперимента происх. эл-ый исход, благоприятствующий соб. А.
Событие
𝛺
наз-ся достоверным,
поскольку
оно происх. в любом эксперименте (всегда).
(т.е.
мн-во, кот. не содержит ни одного элем-го
исхода) наз-ся невозможным
соб, т.к. оно никогда не происх. Все
остальные события, кроме 𝛺
и
,
наз. случайными.
Операции над соб.:
1)
Суммой
событий А и В наз-ся объединение этих
мн-в (А
B).
А
B
–соб., кот. происх. ⇔,
когда происх. хотя бы одно из соб. А или
В.
2)
Произведением
соб. А и В наз-ся пересечение мн-в А и
В(т.е. А
В
или АВ).АВ–происх.⇔
когда А и В происх. одновременно.
3) Разностью соб. А и В наз-ся разность мн-в А\В. А\В происходит <=>, когда происх. А, но не происх. В.
Опр
Если
,
то говорят, что А
влечёт В (В
явл. следствием А)
Опр Соб. А и В наз-ся несовместимыми, если АВ=
Опр
Соб.
наз-ся
противоположным
к соб А. .
происх. ⇔
когда А не происх.
Опр
Говорят, что
соб.
образуют полную
группу, если
.
В частности, соб. А или
образуют полную группу. События
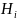наз-ся гипотезами.
Для
событий выпол-ся законы Де-Моргана: 1)
2)
Опр.
вероятности соб.: Предположим,
что пр-во эл-ых исх-ов 𝛺={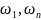
}:
1) конечно
2) все
исходы равновероятны. Т.е.
.
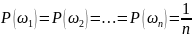Т.о. классическое
опр. вероятности:
Если пр-во эл-ых исх-ов конечно, а все
исходы равновозможны, то вероятностью
соб. А наз-ся отнош. числа исходов
благоприятствующих А к числу всех
возможных исходов, т.е.
№2.Выборки: упорядоченные, неупорядоченные, с возвращением, без возвращения. Размещения, сочетания, перестановки. Свойства сочетаний.
Лемма1:
Из n
эл-ов 1ой группы (
)
и m
2ой группы (
)
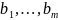можно составить ровно m
n
различных упорядоченных пар, вида: (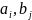
)
содержащих по одному эл-ту из каждой
группы. ◄(
)(
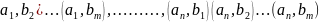-матрица
из n
m
эл-ов►
Лемма2:
Из
эл-ов 1ой группы
можно составить
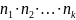различных упорядоченных комбинаций:
содержащих по одному эл-ту из каждого
мн-ва.
Предположим,
что у нас есть мн-во из n
эл-ов {
}.Выбрали
к эл-ов {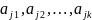
}.
Этот набор наз-ся выборкой
объёма к
из n
эл-ов.
Выборки могут быть: с возвр., без возвр., упор., неупоряд.
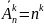(упор.
с возвр.),
(упор.
без возвр.),
(неупор.
с возвр.),
(неупор.
без возвр.)
Упорядоченные выборки без возвр. наз-ся размещениями.
Неупор. выборки без возвр.наз-ся сочетаниями.
Св-ва
сочетаний:
1)
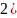
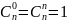3)
4)
Ф-ла
Бинома-Ньютона:
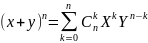
Теор:
Пусть
-целые
неотриц. числа такие, что
.
Тогда число способов, с помощью которых
n
эл-ов можно разбить на к
групп так, чтобы в 1ую группу попало
эл-ов…
в последнюю
:
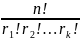-число
способов
№3. Геометрическая вероятность
Предположим, что на отрезок [a,b] наудачу бросается точка, -координата этой точки. Выясним какова вероятность попадания в какую-нибудь конкретную точку. Вероятность попадания в обл-ти одинаковой длины- равны.
От
противного Пусть
событие А-попадание в рациональную
точку.
.
Противоречие с понятием вероятности
события.
Вероятность
попадания в отр. [c,d]
входящий
в [a,b]
будем определять следующим образом:
.
В
общем случае геом.вероятность определяется
следующим образом:
,
где
-мера
Лебега,
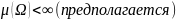
№4. Вероятности достоверного и невозможного событий. Вероятность суммы событий. Вероятность противоположного события. Непрерывность вероятности.
Допустим
монету подбрасывают N
раз. Допустим N(z)-число
выпадений герба. Величина
-относительной
частотой выпадения
герба. Тогда
-
относит. частота соб А. Р(А)-вероятность
соб. А.
1)
2)
Событие
𝛺
наз-ся достоверным,
если оно происходит в результ. Каждого
эксперимента. Тогда
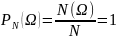
3)
Суммой
событий А и В наз. событие, происх. ⇔
когда происх. или соб. А или соб.В (А
В).
А и В наз. несовместимыми,
если они не могут произойти одновременно.
Тогда обозн. А+В и
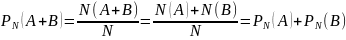
Вер.
противопол. события к А:
.
𝛺=A+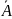
Опр.
Говорят,
что посл-ть мн-в
сх-ся
к мн-ву А снизу
и пишут:
если
.
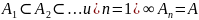Говорят,
что посл-ть
сх-ся
к А сверху
если
.
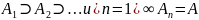Вероятноть
непр-на,
т.е. если
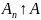или
,
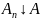то
№5. Условная вероятность как вероятностная мера. Теорема умножения. Независимые события. Свойства независимых событий.
Предположим,
что наступило некоторое соб. А и Р(А)
0.
Выясним какова вероятность наступления
соб. В при усл., что наступило соб. А.
Провели N
экспериментов.
Пусть N(A)-число появлений соб. А, N(AB)-число появл. соб. АВ
-
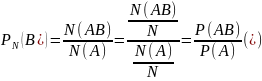ф-ла условной вер. соб. В при усл., что
наступило соб. А
Замеч При фикс. А, Р(В\А)- обыкновенная вероятн.
Из
ф-лы (*) следует, что
-теорема
умножения.
-теор.
умнож. для n
событий
Опр События А и В наз-ся независимыми, если P(AB)=P(A) P(B)
Св-ва независимых соб.:
1)
Любое
событие и соб. имеющее вероятн.=0 –
независимое.
2) Любое соб. и соб., имеющее вер.=1 -независимы .
3) Соб. не зависит от самого себя ⇔ когда его вер.=0 или 1.
4)
Пусть
,
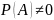тогда А и В- независимы ⇔
когда
5)
Если
А и В-независимы, то
–также независимы.
Опр
События
наз-ся независимыми
в совокупности,
если
… … .. …. …. …. ….. …. … …. …
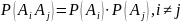
№6. Гипотезы. Формула полной вероятности. Формула Байеса. Априорные и апостериорные события.
Теор
Пусть соб. А может произойти лишь с одним
из событий
.
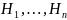Тогда справедлива следующая ф-ла
полной вероятности:
.
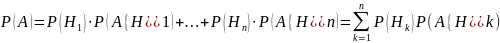◄То,
что соб. А может наступить с одним из
???.
Событие означает, что
►
Замеч.
Ф-ла
полной вер-ти работает даже когда
,
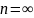а
также когда
-образуют
полную группу.(
)
При этом
наз-ся гипотезами.
Теор.
Пусть
выполнены все условия, при которых
справедлива пред. теор и
.
Тогда имеет место ф-ла
Байеса:
,
где
наз-ся априорными
вер-тями, а
-
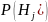апостериорные.
№7. Схема независимых испытаний Бернулли. Формула Бернулли. Полиномиальная схема.
Испытаниями Бернулли наз-ся независимые испытания, в каждом из кот-ых возможны 2 исхода. Вер-ти этих исх-ов не меняются от испыт. к испыт. Назовём два возможных исхода успехом и неудачей(«У» и «Н»). Тогда 𝛺={У,Н}, P(У)=p, P(Н)=q, p+q=1.
Допустим
проведено n
испыт-ий. Нас будет интересовать вер-ть
того, что в результ. этих n
испыт. произошло ровно к
успехов. Обозначим
-число
успехов в n
испыт.
-вер-ть
того, что из n
испыт.
произошло ровно k
успехов.
–ф-ла
Бернулли
Полином.
схема: Предположим,
что проводят n
независимых испытаний в каждом из кот-ых
возможны k
исходов. 𝛺={
}.
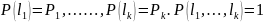Найдём вер-ть того, что 1-ое событие
произошло
раз.
№8. Предельная теорема Пуассона. Локальная предельная теорема Муавра-Лапласа. Интегральная теорема Муавра-Лапласа.
Предельная
теор. Пуассона:
При
таким образом, что
,
тогда
,
т.е. если в схеме Бернулли n
«велико», а р «мало» так, что
и не мало и не велико, тогда
Локальная
предельная теор. Муавра-Лапласа:
Если в схеме Бернулли р не слишком
близко к 0 или к 1, а n
«велико», то
,
где
, а
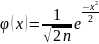
Иинтегр-ая
теор. Муавра-Лапласа:
Пусть 0<p<1
тогда при больших n,
вер-ть того, что
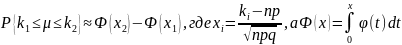
№9
Случайной величиной
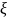называется функция
(w),
отображающая пространство элементарных
исходов Ω во множестве действительных
чисел R.Функцией распределения случайной величины называется функция F(x) действительной переменной х, определяющая вероятность того, что случайная величина примет в результате эксперимента значение, меньшее некоторого фиксированного числа х.
.
.
Если рассматривать как случайную точку на оси ох, то F(x) с геометрической точки зрения—это вероятность того, что случайная точка в результате реализации эксперимента попадет левее точки х.
Свойства функции распределения.
Свойство
1.
.
.Т.к.
F(x)–вероятность
Свойство
2.Функция
распределения F(x)–неубывающая
функция, т.е. для
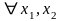таких что x1<x2
.
.
.
Свойство
3.
,
.
Свойство
4.
справедлива формула:
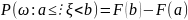.Док-во.
Свойство
5.
.
Зам-е.
Если F(x) непрерывна в т.а, то
Свойство
6.
.
Опр.
Вероятностная мера, заданная на
Борелевских
множеств.
равенством
,
наз-ся распределением случайной величины.
Т-а. Распределение и функции распределения однозначно определяют друг друга.
Опр.Любая ф-я однозначно определяющая ф-ю распределения наз-ся законом распределения случайной величины .
№10.
Случайная величина Х называется дискретной, если она принимает конечное либо счетное число значений, т.е. Ωх—конечно или счетно.
Простейшей формой задания дискретной случайной величины является таблица, в которой перечислены возможные значения случайной величины и соответствующие им вероятности.
|
x1 |
x2 |
… |
xn |
… |
P |
p1 |
p2 |
… |
pn |
… |
Такая таблица называется рядом распределения дискретной случайной величины.
Законом распределения дискретной случайной величины называется совокупность пар чисел вида (хi, рi), где xi—возможные значения случайной величины, а pi—вероятности, с которыми случайная величина принимает эти значения, т.е.
,
причем
.
Говорят, что дискретная случайная величина имеет биномиальное распределение с параметрами (n,p), если она может принимать целые неотрицательные значения
с вероятностями
.
|
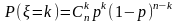0 |
1 |
… |
K |
… |
n |
P |
|
|
… |
|
… |
pn |
Говорят,
что случайная величина
имеет распределение Пуассона с параметром
λ (λ>0), если она принимает целые
неотрицательные значения
с вероятностями
.
|
0 |
1 |
… |
k |
… |
P |
|
|
… |
|
… |
Обозначают
,
т.е. случайная величина Х имеет
распределение Пуассона с параметром
λ.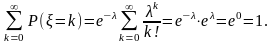
Говорят,
что случайная величина
имеет геометрическое распределение с
параметром р (0<р<1), если она принимает
натуральные значения
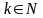с вероятностями
,
где q=1-p.
|
1 |
2 |
3 |
… |
k |
… |
P |
p |
qp |
q2p |
… |
qk-1p |
… |
Очевидно, что вероятности появления значений 1,2,3… образуют геометрическую прогрессию с первым членом р и знаменателем q (0<q<1).
.
№11.
Опр.
Случайная величина
наз-ся абсолютно
непрерывной,
если
неотрицательная
ф-я
называемая плотностью распределения
вероятностей случайной величины
,
такая что
.
Свойства плотности распределения.
.Плотность распределения—неотрицательная функция:
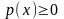.Несобственный интеграл от плотности распределения в пределах от -∞ до +∞ равен единице:
.
Вероятность того, что непрерывная случайная величина примет значение из множества В, равна интегралу по множеству В от плотности распределения.
.
Говорят, что случайная величина равномерно распределена на отрезке [a, b], если она непрерывна и имеет плотность вероятности:
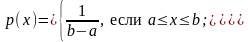
Говорят, что случайная величина имеет показательное (экопоненциальное) распределение с параметром λ>0, если она непрерывна и имеет плотность распределения
;
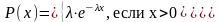обозначают
~M(λ).
Таким
образом
Г
оворят,
что случайная величина
имеет нормальное
распределение с параметрами a,
G2,
если она непрерывна и имеет плотность
.
Обозначение
~N(a,
G2),
те
имеет нормальное распределение с
параметрами a,
G2.
График плотности нормально распределенной случайной величины имеет вид:
№12.
Опр.Вектор
,
где
—случайные
величины, называются многомерным
случайным вектором.
Опр.
Ф-я
наз-ся ф-й
распределения случайного вектора
или ф-й совместного распределения
случайных величин
.
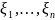Опр.
Вероятная мера
наз-ся распределением случайного
вектора.
.
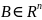Свойства функции распределения случайного вектора.