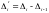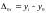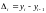Решение.
Данные задачи представляют собой интервальный динамический ряд с заданным интервалом – один год. Все уровни – сопоставимы.
С каждым годом число безработных увеличивается, то есть имеется тенденция роста.
Определим средний уровень числа безработных за данные 5 лет, как среднее арифметическое всех уровней:
.
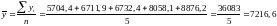Абсолютные приросты, цепные и базисные, темпы роста и прироста, цепные и базисные рассчитываются по формулам:
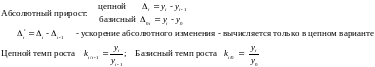
Вычисления удобно проводить в таблице:
Номер периода |
Число безработных млн. чел. Уровни yi |
Абсолютное изменение прироста уровней базисные цепные |
Ускорение абсолютного изменения
|
Темп роста уровня, в % к предыдущему уровню (цепной) |
Темп роста уровня, в % к начальному уровню (базисный) |
|
|
|
|||||
0 начальный |
5704,4 |
|
|
|
|
100,000 |
1 |
6711,9 |
1007,5 |
1007,5 |
|
117,662 |
117,662 |
2 |
6732,4 |
1028 |
20,5 |
-987 |
100,305 |
118,021 |
3 |
8058,1 |
2353,7 |
1325,7 |
1305,2 |
119,691 |
141,261 |
4 |
8876,2 |
3171,8 |
818,1 |
-507,6 |
110,153 |
155,603 |
Если
темпы роста записать в следующем виде:
,
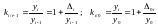то величины
и
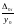будут называться относительным приростом
или темпом прироста.
Добавим в таблицу показатели темпа прироста:
Номер периода |
Число безработных млн. чел. Уровни yi |
Абсолютное изменение прироста уровней базисные цепные |
Ускорение абсолютного изменения
|
Темпы прироста уровня, в % к предыдущему уровню (цепной) |
Темпы прироста уровня, в % к начальному уровню (базисный) |
|
|
|
|||||
0 начальный |
5704,4 |
|
|
|
|
0,000 |
1 |
6711,9 |
1007,5 |
1007,5 |
|
17,662 |
17,662 |
2 |
6732,4 |
1028 |
20,5 |
-987 |
0,305 |
18,021 |
3 |
8058,1 |
2353,7 |
1325,7 |
1305,2 |
19,691 |
41,261 |
4 |
8876,2 |
3171,8 |
818,1 |
-507,6 |
10,153 |
55,603 |
Абсолютное значение 1% прироста равно сотой части предыдущего, или базисного, уровня. То есть, для нашей задачи 1% прироста равен 5704,4/100 = 57,044.