Статистика Вариант 8

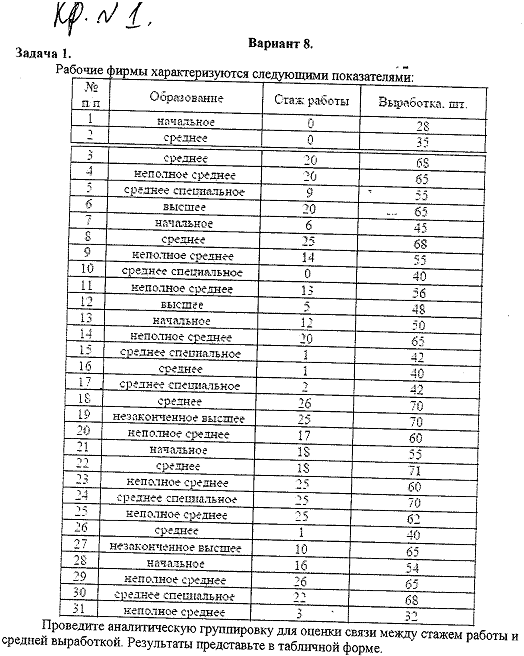
Решение.

Определим переменные задачи: пусть Y – выработка деталей, X - стаж работы.

Разбиение данных на группы (интервалы) можно провести не одним образом. Чаще всего встречаются равноинтервальное и равночастотное разбиения.

По смыслу задачи средняя выработка деталей рабочим зависит от стажа, поэтому будем анализировать именно данные по выработке. Равночастотное (то есть с одинаковым количеством переменных в каждом интервале) разбиение не годится, так как данные не равномерны и такое разбиение может исказить закономерность распределения.

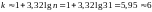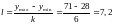Для равноинтервального разбиения определим число интервалов по формуле Стерждеса: интервалов. Тогда величина (длина) интервала будет равняться , а начала и концы интервалов определятся следующим образом:

Разбиение по Y
начало интервала	конец интервала
28	35,2
35,2	42,4
42,4	49,6
49,6	56,8
56,8	64
64	71,2

Запишем данную таблицу, отсортировав данные от 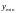до 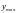, и посмотрим наложение вычисленных интервалов на данные:

n	стаж	выработка	интервал
1	0	28	1
2	3	32
3	0	35
4	0	40	2
5	1	40
6	1	40
7	1	42
8	2	42
9	6	45	3
10	5	48
11	12	50	4
12	16	54
13	9	55
14	14	55
15	18	55
16	13	56
17	17	60	5
18	25	60
19	25	62
20	20	65	6
21	20	65
22	20	65
23	10	65
24	26	65
25	20	68
26	25	68
327	22	68
428	26	70
29	25	70
30	25	70
31	18	71

Для каждого интервала вычислим средние значения стажа и выработки по формулам:

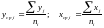и результаты поместим в таблицу (ni – частота наблюдений, то есть, сколько переменных содержит данный интервал, сумма ):

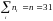n	стаж	выработка	интервал	ni	Yi	Xi
1	0	28	1	3	32	1
2	3	32
3	0	35
4	0	40	2	5	41	1
5	1	40
6	1	40
7	1	42
8	2	42
9	6	45	3	2	47	6
10	5	48
11	12	50	4	6	54	14
12	16	54
13	9	55
14	14	55
15	18	55
16	13	56
17	17	60	5	3	61	22
18	25	60
19	25	62
20	20	65	6	12	68	21
21	20	65
22	20	65
23	10	65
24	26	65
25	20	68
26	25	68
327	22	68
428	26	70
29	25	70
30	25	70
31	18	71

Или:

интервал	ni	Yi	Xi
1	3	32	1
2	5	41	1
3	2	47	6
4	6	54	14
5	3	61	22
6	12	68	21

Первый и второй столбец можно объединить – значения по стажу одинаковы. Получаем окончательное разбиение, то есть построили вариационный ряд для дальнейшего анализа данных.

Номер интервала	ni – частота	Yi – выработка	Xi – стаж
1	3+5=8	(32+41)/2=37	(1+1)/2=1
2	2	47	6
3	6	54	14
4	3	61	22
5	12	68	21

РЕШЕНИЕ.

Средний фактический выпуск продукции по всем трём заводам определим как среднюю арифметическую выпусков (наиболее распространенное среднее в статистике):

.

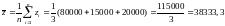Среднюю выработку одним рабочим вычислим по аналогичной формуле:

.

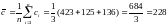РЕШЕНИЕ

Относительные величины структуры характеризуют долю отдельных частей в общем объеме совокупности и выража­ются в долях единицы или в процентах. Они исчисляются по сгруппированным данным. Общий объём расходов 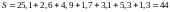млн. руб. Определим относительные величины структуры затрат, как доли в процентах:

Основные сырье и материалы - ;

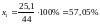Вспомогательные материалы - ;

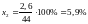Топливо - ;

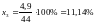Энергия - ;

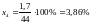Амортизация - ;

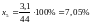Заработная плата и отчисления

на соцстрахование - ;

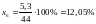Прочие расходы - .
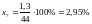