Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Одесский национальный университет им. И.И. Мечникова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

cryptology_konspekt.doc

Скачиваний:

Добавлен:

01.03.2025

Размер:

3.09 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1712 13 14 15 16 17 > Следующая >>>

Раздел одиннадцатый

1. Эллиптические кривые. Группа точек кривой.

Криптографические приложения теории эллиптических кривых – очень молодой раздел в криптографии. Его появление диктуется необходимостью поиска задач такой вычислительной сложности, которая бы гарантированно обеспечивала стойкость криптографических объектов. N. Koblitz был одним из авторов идеи использования эллиптических кривых в данной области. Главным здесь явилось использование группы точек кривой в том же качестве, в котором теоретико-групповые объекты присутствуют в двухключевой криптографии. Эта группа, вообще говоря, не является циклической. От сюда возникают надежды на усложнение вычислительных задач, связанных с такой группой.

Обозначим через К некоторое поле. Нас будут интересовать прежде всего поля: R вещественных чисел, Q – рациональных чисел и F , имеющее элементов.

Определение. Пусть К будет полем характеристики 2, 3 и пусть , где

К, многочлен третьей степени, не имеющий кратных корней. Тогда эллиптической кривой над полем К называется множество точек (x, y), где К, удовлетворяющих уравнению

, (11.1)

вместе с элементом, обозначаемым через О и называемым «бесконечно удаленной точкой» (о котором будет сказано далее).

Эллиптические кривые определяются над различными полями, покажем особенность точек эллиптической кривой, множество которых образует абелеву группу и для наглядности будем считать, что К = R, т.е. эллиптическая кривая есть обычная кривая на плоскости ( вместе с “точкой О в бесконечности”).

Определение. Пусть Е будет эллиптической кривой над полем вещественных чисел, и P и Q будут точками этой кривой. Определим точку противоположную Р и сумму Р + Q следующим образом:

1) Если Р есть точка в бесконечности О, то определим – Р = О и Р + Q = Q; далее точка О служит нейтральным элементом (или нулем) группы точек. В дальнейшем полагаем, что ни Р, ни Q не являются точками в бесконечности.

2) Противоположный элемент – Р есть точка с той же координатой х, что и Р, однако с противоположной координатой y, т.е. – (x, y) = (x, -y). Из уравнения (11.1) с очевидностью вытекает, что если точка (x, y) лежит на кривой, то и точка (x, -y) также лежит на этой кривой.

3) Если точки Р и Q имеют различные координаты х, то нетрудно заметить, что прямая l = пересекает кривую еще точно в oдной точке R (разве только эта прямая является касательной к кривой в точке Р и тогда берем R = P или является касательной в точке Q и тогда берем R = Q). В качестве суммы Р + Q берем точку – R, т.е. точку симметричную (относительно оси х) к той третьей точке пересечения. Геометрическая конструкция точки P + Q показана на рис.1 ниже.

4) Если Q = - P (т.е. точка Q имеет ту же координату х и противоположную координату у), то определим P + Q = O (точка в бесконечности). (См. условие (2))

5) Остается последняя возможность Р = Q. Пусть прямая l будет касательной к кривой в точке Р, и пусть R будет единственной точкой пересечения прямой l с кривой, отличной от Р. Тогда определим Р + Q = - R. (Если прямая l является «двойной касательной» к кривой, т.е. точка Р является точкой перегиба кривой, то в качестве R берем саму точку Р.)

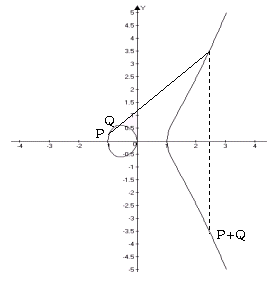
Пример. Эллиптическая кривая, отвечающая уравнению на плоскости, представлена на рисунке справа. На нем изображен типовой случай сложения двух

точек Р и Q. Рисуем секущую, проходящую

через точки Р и Q и в качестве Р + Q берем

точку, симметричную (относительно оси х)

к третьей точке пересечения прямой, прохо-

дящей через Р и Q с кривой. Если точки Р и

Q совпадают, т.е. когда ищется точка 2Р, ри-

суем прямую, касательную к кривой, в точке

Р; тогда точкой 2Р является точка, симмет-

ричная к третьей точке, в которой эта каса-

тельная пересекает кривую.

Покажем теперь, почему существует лишь

одна точка, в которой прямая l, проходящая

через точки Р и Q, пересекает кривую; един-

ственность определяет выражение для коор-

динат этой третьей точки, а затем и выраже-

ние для координат суммы Р + Q.

Пусть ( ), ( ) и ( ) означают соответственно координаты точек P, Q и P + Q. Требуется выразить и через координаты , , и . Допустим, что находимся в условиях случая (3) определения суммы P + Q и пусть х + будет уравнением прямой, проходящей через точки P и Q (в случае (3) эта прямая не перпендикулярна оси х). Тогда и . Точка прямой l, т.е. точка ( ) лежит на эллиптической кривой тогда и только тогда, когда == . Таким образом, для каждого корня уравнения третьей степени

существует единственная точка пересечения. Известны, однако, два корня этого уравнения: и , где и являются координатами точек P и Q, лежащих на этой кривой. Поскольку сумма корней приведенного уравнения третьей степени есть число противоположное коэффициенту при , то третьим корнем этого уравнения является . Проводя вычисления для и P +Q = получаем выражения, зависящие от и :

;

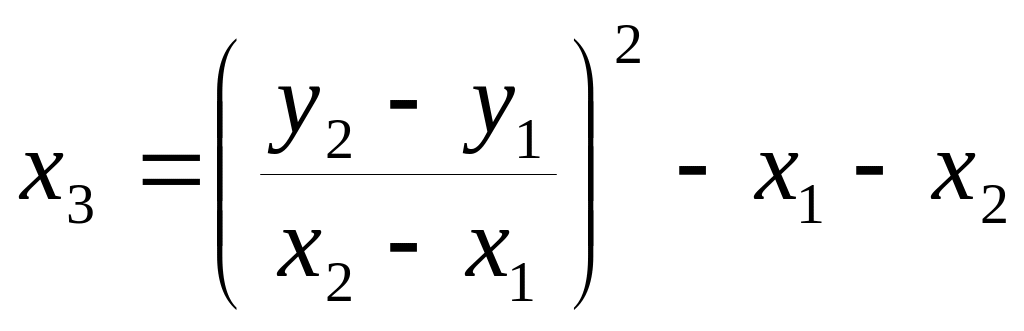(11.2)

Случай (5), где P = Q, подобен этому с тем лишь, что коэффициент теперь равен

производной в точке Р. Дифференцирование функции, заданной в уравнении (11.1), приводит к выражению , из которого получаем следующие выражения для координат точки 2Р:

;

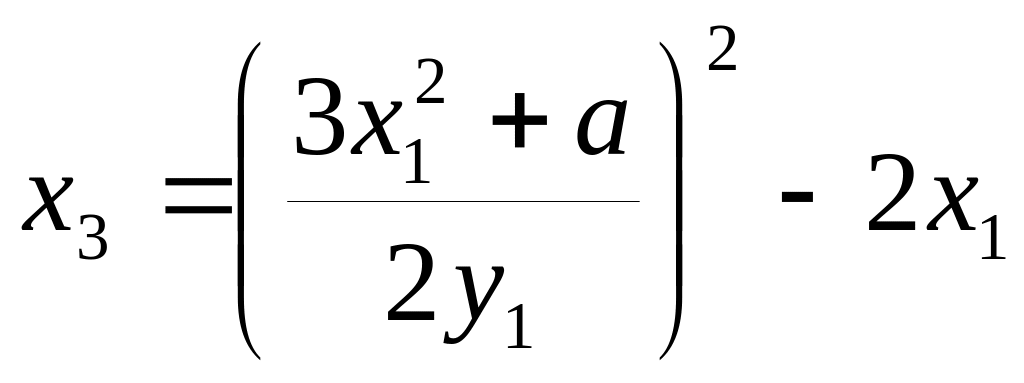(11.3)

Пример. Пусть Р = (-3 , 9) и Q = (-2 , 8) будут точками кривой, заданной уравнением . Найдем точки Р + Q и 2Р.

Решение. Подставим в первое из выражений (11.2). Получим ; тогда второе из выражений дает . Далее, подставим в первое из выражений (11.3) и получим 25/4 как координату х точки 2Р; координата y = -35/8 получается из второго выражения (11.3).

Теорема. Множество точек эллиптической кривой над полем К относительно операции сложения, определенной выше, образует абелеву группу.

Существует несколько способов доказательства того, что определение операции сложения точек эллиптической кривой наделяет указанное множество структурой абелевой группы. Но эту теорему доказывать не будем.

Так же, как и в случае произвольной абелевой группы, под nP будем понимать результат сложения точки Р с самой собой n раз, если n является положительным числом, в противном случае – это результат сложения точки –Р с самой собой |n| раз.

Скажем несколько слов о «точке в бесконечности» О. Из определения ясно, что она является нейтральным элементом группы. На нашем рисунке ее можно вообразить как точку, лежащую бесконечно далеко на оси y, предельного положения касательных к кривой. Она является «третьей точкой пересечения» каждой вертикальной прямой, пересекающей кривую; такая прямая пересекает кривую в точках вида ( , ( и О.

Определение. Порядок N точки Р, лежащей на эллиптической кривой, есть такое наименьшее натуральное число, что NP = O.

Очевидно, что такое число может не существовать. Часто важно знать точки конечного порядка на эллиптической кривой, определенной над полем Q.

Пример. Определим порядок точки Р = (2, 3) на кривой .

Решение. Используя соотношения (5), получим 2Р = (0, 1); используя эти соотношения еще раз, получим 4Р = 2(2Р) = (0, -1). Так что 4Р = -2Р, откуда получаем, что 6Р = О. Таким образом, порядок Р может быть 2, 3 или 6. Но 2Р = (0, 1) О, а если бы порядок был бы равен 3, то имели бы, что 4Р = Р, что, однако, неверно. Так что точка Р имеет порядок 6.

2. Эллиптические кривые над конечным полем.

До конца этого раздела К будет конечным полем F , имеющем элементов. Пусть Е будет эллиптической кривой, определенной над полем F . Легко заметить, что эллиптическая кривая Е может иметь самое большее 2q + 1 F -точек: точка в бесконечности и 2q пар , причем F , удовлетворяющих уравнению (11.1). Видно, что для каждого из q возможных значений х существует не более двух значений у, которые удовлетворяют уравнению (11.1).

Однако, поскольку только половина ненулевых элементов поля F имеют квадратные корни, можно было ожидать, что (считая случайным элементом этого поля) количество F - точек на кривой в два раза меньше. Подробнее, пусть будет квадратичным характером поля F . Это отображение, которое каждому элементу х F сопоставляет , в зависимости от того, имеет ли х квадратный корень в F (и, кроме того, ). Например, если q = p – нечетное простое число, то есть символ Лежандра. Далее, число решений у F уравнения всегда равно , а число решений уравнения (11.1) (вместе с точкой на бесконечности) есть

. (11.4)

Можно ожидать, что значение будет одинаково часто равняться +1 и –1.

Эта сумма напоминает суммирование в «случайном шаге»: бросается q раз монета, при выпадении орла делаем шаг вперед, при выпадении решки – шаг назад. Используя метод теории вероятностей, можно вычислить, что при q бросках монеты среднее значение, на которое отойдем, таким образом, от наивысшей величины, имеет порядок . Сумма