Задание 1

1.2Совхоз для кормления животных использует два вида корма. В дневном рационе животного должно содержаться не менее 6 единиц питательного вещества А и не менее 12 единиц питательного вещества В. Какое количество корма надо расходовать ежедневно на одно животное, чтобы затраты были минимальными?

Питательное вещество	Количество питательных веществ в 1 кг корма
	1	2
А	2	1
В	2	4
Цена 1 кг корма, тыс.руб.	0,2	0,3

Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решить задачу на максимум и почему?

Решение

Пусть:

х₁ – количество корма «1»

х₂ – количество корма «2»

Целевая функция:
min z = 0,2 ∙ x1 + 0,3 ∙ x2	т.е. необходим минимум затрат на корма
2 ∙ x1 + x2 ≥ 6	т.е. из всего объема потребляемых кормов, вещества «А» должно быть не менее 6 единиц
2 ∙ x1 + 4 ∙ x2 ≥ 12	т.е. из всего объема потребляемых кормов, вещества «А» должно быть не менее 6 единиц
x1; x2 ≥ 0	Количество потребляемых кормов не может быть отрицательным

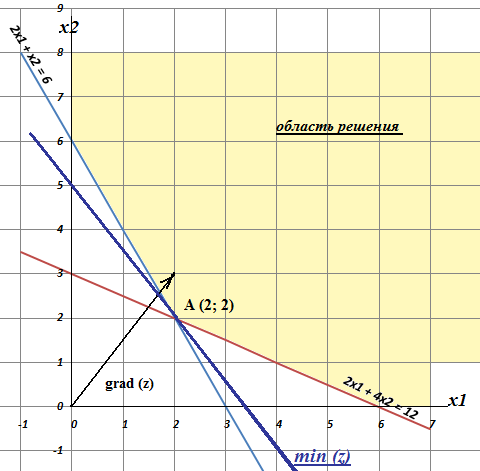
Определим по графику минимальное значение функции z:

2 ∙ x1 + x2 = 6

2 ∙ x1 + 4 ∙ x2 = 12

Решение системы: x₁ =2

x₂ = 2

Минимальные затраты: z = 0,2 ∙ 2 + 0,3 ∙ 2 = 1

Таким образом, минимальные затраты на корм составляют 1 тыс.руб. и возможны при использовании 2 ед. корма «А» и 2 ед. корма «Б».

Решение задачи на максимум приведет к решению +∞, т.к график сверху справа не ограничен.

Решить графическим методом типовую задачу оптимизации.

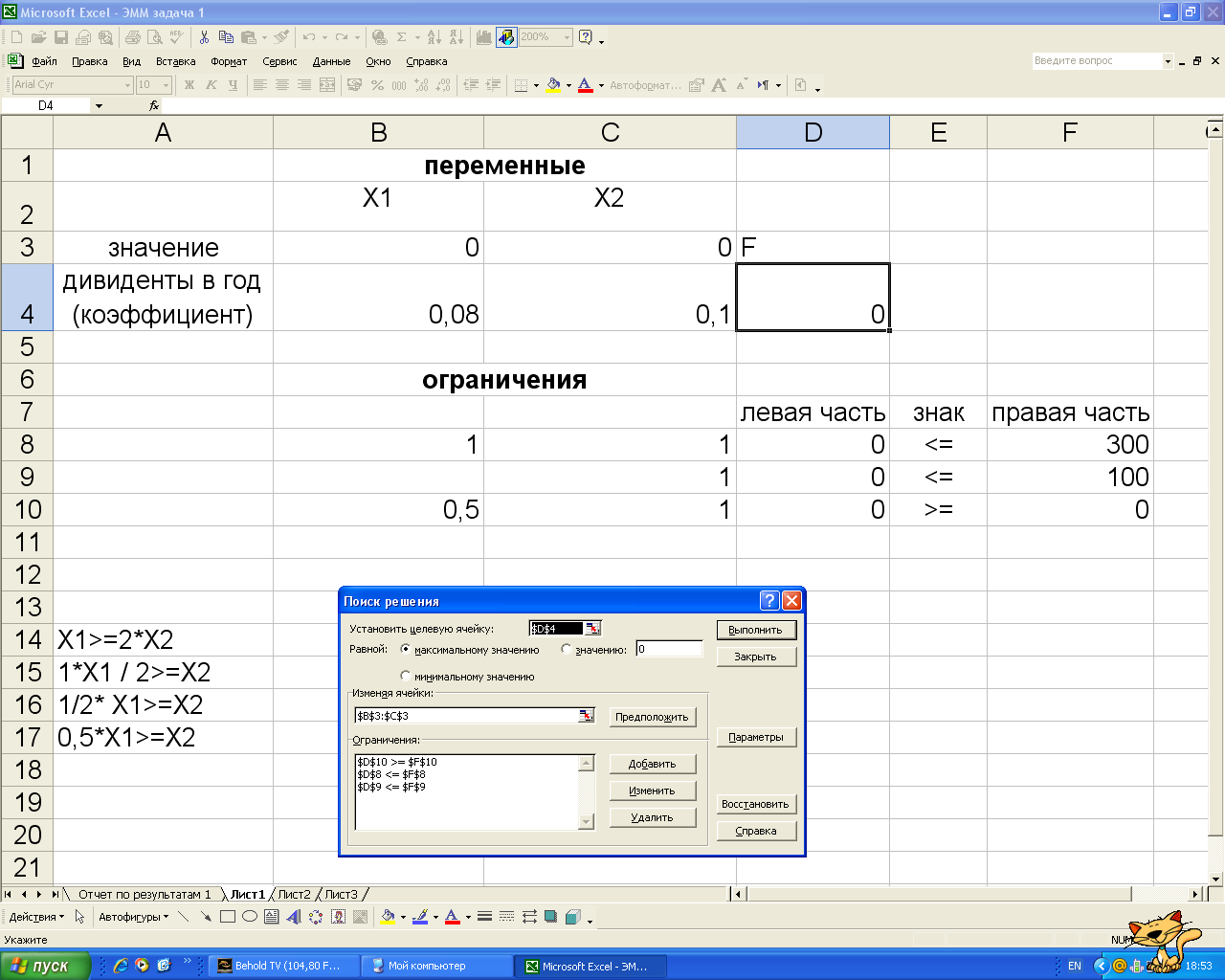
Инвестор, располагающий суммой в 300 тыс. ден. ед., может вложить свой капитал в акции автомобильного концерна А и строительного предприятия В. Чтобы уменьшить риск, акций А должно быть приобретено на сумму по крайней мере в два раза большую, чем акций В, причем последних можно купить не более чем на 100 тыс. ден. ед.

Дивиденды по акциям А составляют 8% в год, по акциям В — 10%. Какую максимальную прибыль можно получить в первый год?

Построить экономико – математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решить задачу на минимум, и почему?

Решение:

Введем обозначения:

х₁ — тысяч ден. ед. может вложить инвестор в акции автомобильного концерна А.

х₂ — тысяч ден. ед. может вложить инвестор в акции строительного предприятия В.

1) Экономико-математическая модель задачи будет иметь вид:

8% =0,08, 10% = 0,1

Построим ОДР задачи:

I.

х1	х2
0	300
300	0

Прямая проходит через точки (0;300) и (300;0).

О(0;0): 0 + 0 – верно, входит в ОДР;

II. ,

х1	х2
200	100
0	0

Прямая проходит через точки (200; 100) и (0;0).

О(1;0): 1-2 0 – верно, входит в ОДР;

III.

х1	х2
0	100

Прямая проходит через точку (0; 100) и параллельна оси ОХ.

О(0;0): 0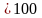 - верно, входит в ОДР.

ОДР задачи это треугольник ОАВ.

Искомая область может находиться только в 1 четверти декартовой системы, т.к. .

2) Определим оптимальные точки задачи: т. max и т. min. Для этого используем линии уровня целевой функции, это прямые заданные уравнением (рис.1).

Для определения направления движения к оптимуму, построим вектор-градиент С.

Координаты вектора являются частными производными целевой функции, т.е. (0,08;0,1). Чтобы построить вектор, нужно соединить эту точку с точкой начала координат. Для удобства строим вектор, пропорциональный вектору С. Он имеет координаты (80;100).

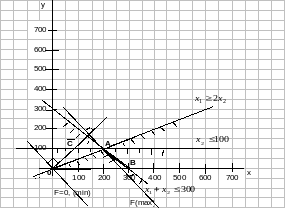
Рис.1

Перпендикулярно этому вектору С через начало координат проводим линию нулевого уровня целевой функции. При максимизации ЦФ необходимо перемещать линию уровня в направлении вектора, а при минимизации – в противоположном направлении.

Предельными точками являются соответственно т. А(max) и т.О(min).

т.О(0;0), т.к. это точка начала координат.

Определим координаты т.А, являющейся точкой пересечения всех прямых. Для этого решим систему, состоящую из 3-х уравнений:

.

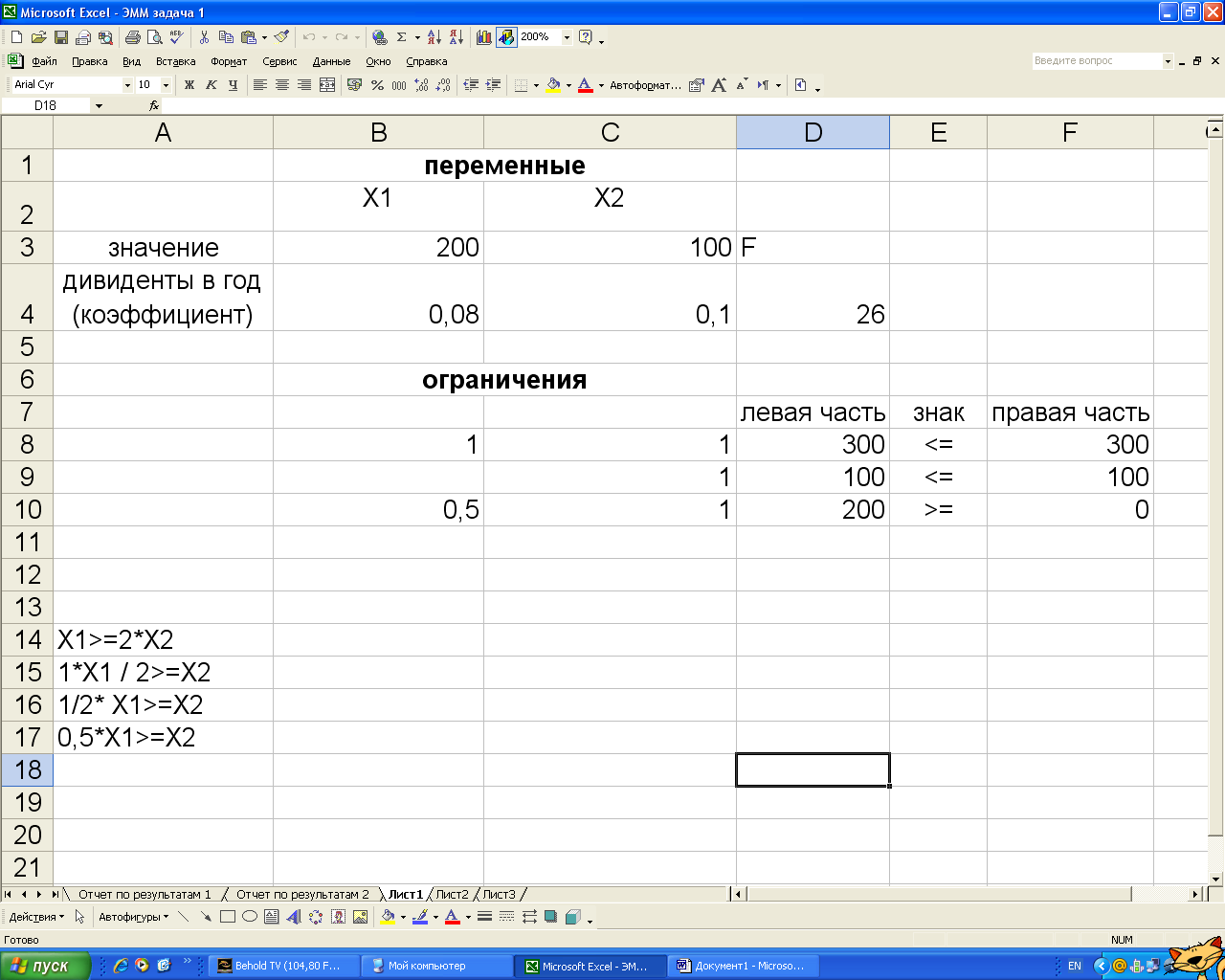
Отсюда: 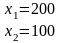А(200;100).

3) Определим оптимальное значение функции:

F max = 0,08*200+0,1*100=16+10=26 (тысяч ден. ед.) – максимальная прибыль, которую можно получить в 1 год по акциям.

Если поставить задачу минимизации, функциональную линию уровня необходимо смещать в направлении противоположном вектору-градиенту С. Минимум целевой функции достигается в точке О(0;0), следовательно, можно записать min (F) = 0 и достигается при   x_{1 =} 0;  x₂ = 0. Значит, минимальная прибыль в 1 год составит 0 тыс. ден. ед.

Ответ: max (F) =26 и достигается при   x₁ =200;  x₂ =100; 

Рекомендуется вложить в акции автомобильного концерна А, 200 тыс. ден. ед., в акции строительного предприятия В, 100 тыс. ден. ед., в первый год получим максимум прибыли 26 тыс. ден. ед.

Расчет в Excel:

Решить графическим методом типовую задачу оптимизации

Продукция двух видов (краска для внутренних (I) и наружных (E) работ) поступает в оптовую продажу. Для производства красок используется два исходных продукта – А и В. Максимально возможные суточные запасы этих продуктов составляют 6 8 тонн соответственно. Расходы продуктов А и В на 1 т соответствующих красок приведены в таблице.

Исходный продукт	Расход исходных продуктов на тонну краски, т		Максимально возможный запас, т
	Краска Е	Краска I
А	1	2	6
В	2	1	8

Изучение рынка сбыта показало, что суточный спрос на краску I никогда не превышает спроса на краску Е более чем на 1т. Кроме того, установлено, что спрос на краску I не превышает 2 т в сутки. Оптовые цены одной тонны красок равны 3000 ден.ед. для краски Е и 2000 ден.ед. для краски I. Какое количество краски каждого вида должна производить фабрика, чтобы доход от реализации продукции был максимальным?

Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решать задачу на минимум, и почему?

Решение

Введем следующие переменные:

Х1 – количество краски Е (т);

Х2 – количество краски I (т).

 Цена  краски Е составляет 3000 (ден. ед.), а цена краски I –2000 (ден. ед.).  Необходимо максимизировать  целевую функцию:

Введены следующие ограничения:

Х1+2Х2≤6;

2Х1+Х2≤8;

Х2≤2;

Х2-Х1≤1.

Первое ограничение по продукту А Х1+2Х2≤6. Прямая Х1+2Х2=6  проходит через точки (0;3) и (6;0).

Второе ограничение по продукту В 2Х1+Х2≤8. Прямая 2Х1+Х2=8 проходит через точки (0;8) и (4;0).

Третье ограничение Х2≤2. Прямая L: Х2=2 проходит параллельно оси Х1 через точку Х2=2.

Четвертое ограничение Х2-Х1≤1. Прямая С: Х2-Х1=1 проходит через точки (0;1) и (-1;0).

Построим вектор целевой функции (градиент, вектор нормали). Координаты конца вектора определяются коэффициентами функции цели, при этом начало вектора находится в точке (0,0): с = (3000,2000). Для удобства можно строить вектор, пропорциональный найденному вектору с = (3,2).

 Построим линию уровня целевой функции. Для этого приравняем целевую функцию к постоянной величине α: 3000Х1  + 2000Х2 = α. Пусть для удобства α = 0, тогда уравнение линии нулевого уровня L0: 3Х1 + 2Х2  = 0 и она проходит через точку (0,0) и (-2,3). Если построение выполнено правильно, то линии уровня целевой функции и градиент перпендикулярны.

 Решением каждого неравенства системы ограничений ЗЛП является полуплоскость, содержащая граничную прямую и расположенная по одну сторону от нее. Пересечение полуплоскостей, каждая из которых определяется соответствующим неравенством системы, называется областью допустимых решений.

Рис. 1.1

Решением  неравенств будет являться полуплоскость, лежащая ниже пересекающихся прямых Х1+2Х2=6, 2Х1+Х2=8, Х2=2, Х2-Х1=1.

При максимизации функции линия уровня перемещается по направлению  вектору – градиенту.

Определим оптимальное решение задачи.

Для решения задачи на максимум переместим линию нулевого уровня L0 параллельно самой себе в направлении вектора с до точки выхода из допустимой области, таким образом, найдем разрешающую точку Д.

Найдем координаты точки Д, которая является пересечение прямых А и В. Решим систему уравнений этих прямых:

  Х1+2Х2=6

2Х1+Х2=8

Находим, что Х1=3,33, Х2 = 1,33

(ден. ед.)

Ответ:

Прибыль фирмы будет максимальной, т.е. 12650 ден. ед., если ежедневно будет производиться 3,33 т краски Е и 1,33 т краски I. 

При решении задачи на минимум – решений не будет.

Задание 2