6.Определение критического пути. Построение линейных диаграмм.

Если продолжительность работы принять за длину соответствующей дуги сетевого графика, то критическим можно назвать путь максимальной длины от входа до выхода графика. Длина этого пути определяет критическое время выполнения проекта, т.е. минимальное время, в пределах которого коллектив исполнителей в состоянии выполнить весь комплекс работ сетевого графика.

Пусть для определенности начальное событие имеет номер 0 и конечное - номер N. Обозначим через L_j длину пути наибольшей протяженности от события 0 до события j.

По известному принципу оптимальности

Величина L_j соответствует наиболее раннему возможному времени T_j⁰ наступления j-го события, т.е. самому раннему сроку завершения всех работ, предшествующих этому событию. Значение L_N cоответствует критическому времени выполнения проекта T_крит.

Обозначим через M_i длину пути наибольшей протяженности от события i до события N. Тогда по тому же принципу

Величина T_i¹ = T_крит - M_i соответствует наиболее позднему допустимому времени наступления i - го события, т.е. самому позднему сроку начала всех работ, последующих за этим событием. Совершенно очевидно, что для событий на критическом пути самое раннее и самое позднее времена их наступления будут совпадать.

Рассмотрим сетевой график (рис. 4):

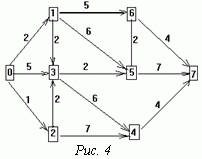
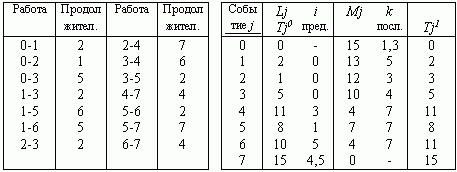
Здесь рассчитываем значения L_j в порядке роста номеров:

L₀=0; L₁ = 2(i=0); L₂ =1(i=0); L₃ = max[L₀+5, L₁+2, L₂+2]=5 (i=0) и т.д.

Затем рассчитываем значения M_i в порядке убывания номеров:

M₇=0; M₆=4 (k=7); M₅=max [2+M₆, 7+M₇] = 7(k=7); M₄ =4 (k=7); M₃ =max[6+M₄, 2+M₅]=10 (k=4) и т.д.

В итоге имеем информацию о наиболее ранних и наиболее поздних моментах наступления событий и индексы предшествующих и последующих событий в самых длинных путях, проходящих через данное событие.

По информации из колонок 3 или 5 можно выявить критические пути с длиной 15: [ 0 - 1 - 5 - 7 ] и [ 0 - 3 - 4 - 7 ].

Очевидно, что работы, не лежащие на критических путях, обладают резервами времени - их выполнение при некоторых условиях может быть задержано на какое-то время. Cуществуют 4 вида резервов:

1. Полный резерв R_ij = T_j¹ - T_i⁰ - T_ij,

2. Свободный резерв R_ij = T_j⁰ - T_i⁰ - T_ij,

3. Независимый резерв R_ij =max [ T_j⁰ - T_i¹ - T_ij, 0],

4. Частный резерв R_ij = T_j¹ - T_i¹ - T_ij.

Так полный резерв работы можно понимать как время, на которое можно замедлить выполнение работы, если предшествующие работы завершатся к самому раннему возможному сроку, но комплекс последующих работ будет выполняться в кратчайший возможный срок. Независимый резерв предполагает завершение предшествующих работ к самому позднему, но начало последующих в самый ранний срок.

Результаты обработки приведенного сетевого графика можно представить следующей таблицей:

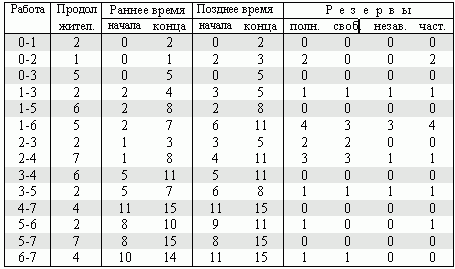
Полученные данные позволяют выделить т. н. подкритические работы, т.е. работы, лежащие на путях, отличающихся по длине от критического не более чем на заданную величину. Основной характеристикой здесь может служить полный резерв.